codeforces 782B The Meeting Place Cannot Be Changed (三分)

The Meeting Place Cannot Be Changed

Problem Description

The main road in Bytecity is a straight line from south to north. Conveniently, there are coordinates measured in meters from the southernmost building in north direction.

At some points on the road there are n friends, and i-th of them is standing at the point x_i meters and can move with any speed no greater than v_i meters per second in any of the two directions along the road: south or north.

You are to compute the minimum time needed to gather all the n friends at some point on the road. Note that the point they meet at doesn't need to have integer coordinate.

Input

The first line contains single integer n (2 ≤ n ≤ 60 000) — the number of friends.

The second line contains n integers x₁, x₂, ..., x_n (1 ≤ x_i ≤ 10⁹) — the current coordinates of the friends, in meters.

The third line contains n integers v₁, v₂, ..., v_n (1 ≤ v_i ≤ 10⁹) — the maximum speeds of the friends, in meters per second.

Output

Print the minimum time (in seconds) needed for all the n friends to meet at some point on the road.

Your answer will be considered correct, if its absolute or relative error isn't greater than 10^- 6. Formally, let your answer be a, while jury's answer be b. Your answer will be considered correct if 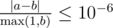holds.

Examples Input

3
7 1 3
1 2 1

Examples Output

2.000000000000

Examples Input

4
5 10 3 2
2 3 2 4

Examples Output

1.400000000000

Note

In the first sample, all friends can gather at the point 5 within 2 seconds. In order to achieve this, the first friend should go south all the time at his maximum speed, while the second and the third friends should go north at their maximum speeds.

题目链接：http://codeforces.com/problemset/problem/782/B

---

题意：一条线上有n个人，每个人一个坐标值xi，每个人有一个最大行走速度vi，问如果要让这n个人走到线上某一个点，最少需要多少时间。(百度的)

思路：(自己的)

知道这个后就明朗了，我们只需要利用3分法(为什么用3分法 o.o 学长说的)循环去缩小那个最小的时间范围。

三分的代码很简洁明了，自己看楼。

接着要解决的一个难题 就是 怎么判断 某t 时间内，所有点是否都能移动到某个点上:

思路：

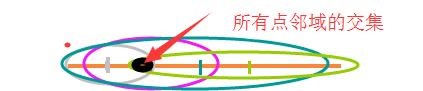
= =。图是丑了点。 每个圈都代表每个人在 某t 时间内的可以的运动范围。

如果交集不为空，则 在t时间内能够移动一点上。

代码实现见函数  bool run(double time)；

ps: 最后输出的时候 用cout<<r<<endl； 或printf("%lf\n",r); 会WA。

因为 这样输出是默认 输出保留小数点6位后输出 即四舍五入 到小数点后6位再输出的。。。坑死我了。。。

---

AC代码如下：time:139ms

 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 #include <cmath>
 using namespace std;
 const int MAXN=+;
 const double eps=0.000001;
 struct type_1
 {
     double x,v;//x 为人的坐标 v为速度
 }people[MAXN];
 int n=;
 bool cmp(type_1 a,type_1 b)
 {
     return a.x<b.x;
 }
 void time(double &maxtime)//求[0,maxtime]中的maxtime
 {
     maxtime=(people[n-].x-people[].x)/people[].v;
     double m;
     for(int i=;i<n;i++)
     {
         m=max((people[i].x-people[].x)/people[i].v,(people[n-].x-people[i].x)/people[i].v);
         if(m>maxtime)
             maxtime=m;
     }
 }
 bool run(double time)//判断t时间内是否都能到某个点
 {
     double x1,x2,temp1,temp2;
     x1=people[].x-people[].v*time;
     x2=people[].x+people[].v*time;
     for(int i=;i<n;i++)
     {
         temp1=people[i].x-people[i].v*time;
         temp2=people[i].x+people[i].v*time;
         if(temp1>x1)
             x1=temp1;
         if(temp2<x2)
             x2=temp2;
         if(x1>x2)
             return false;
     }
     return true;
 }

 int main()
 {
     cin>>n;
     for(int i=;i<n;i++)
         scanf("%lf",&people[i].x);
     for(int i=;i<n;i++)
         scanf("%lf",&people[i].v);
     sort(people,people+n,cmp);
     double l=,r;//时间范围[0,maxtime]
     time(r);
     double o1,o2;//三分后的两个点
     bool bo1,bo2;
     while(l+eps<r)//缩小到精度以内 结束循环。
     {
         o1=(*l+r)/;//时间三分后的time1
         o2=(*r+l)/;//时间三分后的time2
 //printf("[%.10lf,%.10lf] [%.10lf,%.10lf]\n",o1,o2,l,r);
         bo1=run(o1);//纪录o1时间内所有点能否到达一点的真假
         bo2=run(o2);
 //cout<<"-"<<bo1<<" "<<bo2<<"-"<<endl;
         if(bo2==false)
             l=o2;
         else
         {
             r=o2;
             if(bo1==true)
                 r=o1;
             else
                 l=o1;
         }
     }
     printf("%.10llf\n",r);//注意 在这里WA了半个多小时，最后加了 (.10) 后终于AC。
     //cout<<r<<endl;
     return ;
 }

2017-03-09 01:16:21