Android -- 贝塞尔使圆渐变为桃心

1，我们上一篇介绍了贝塞尔曲线推到原理和在Android里的简单使用，今天就和来写写贝塞尔曲线的实际应用，今天实现的效果图如下：

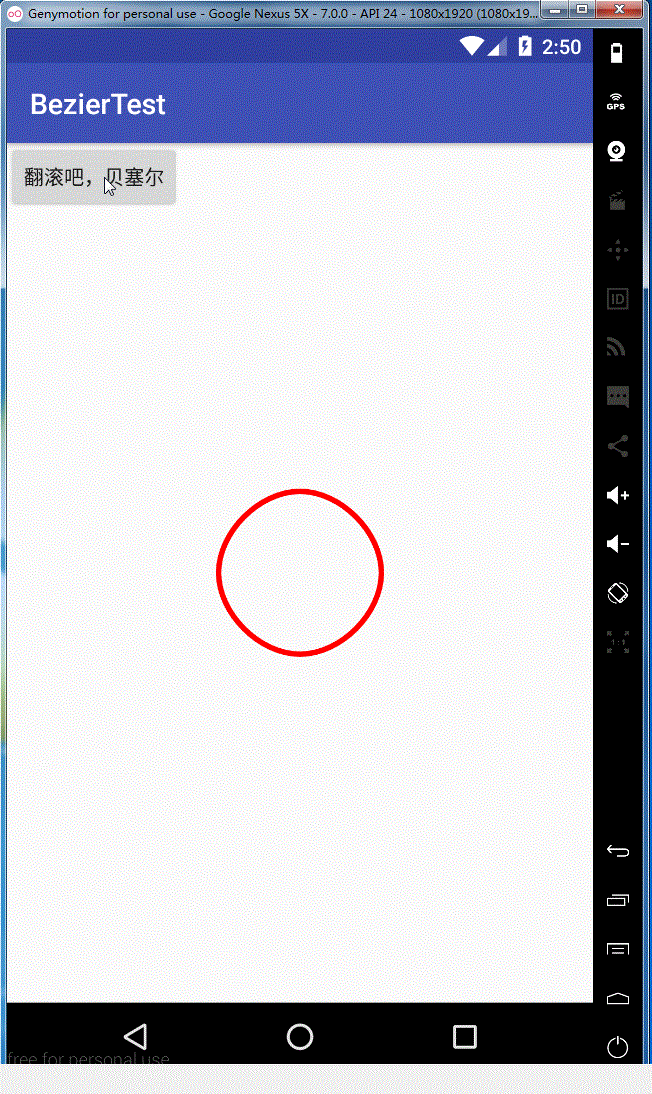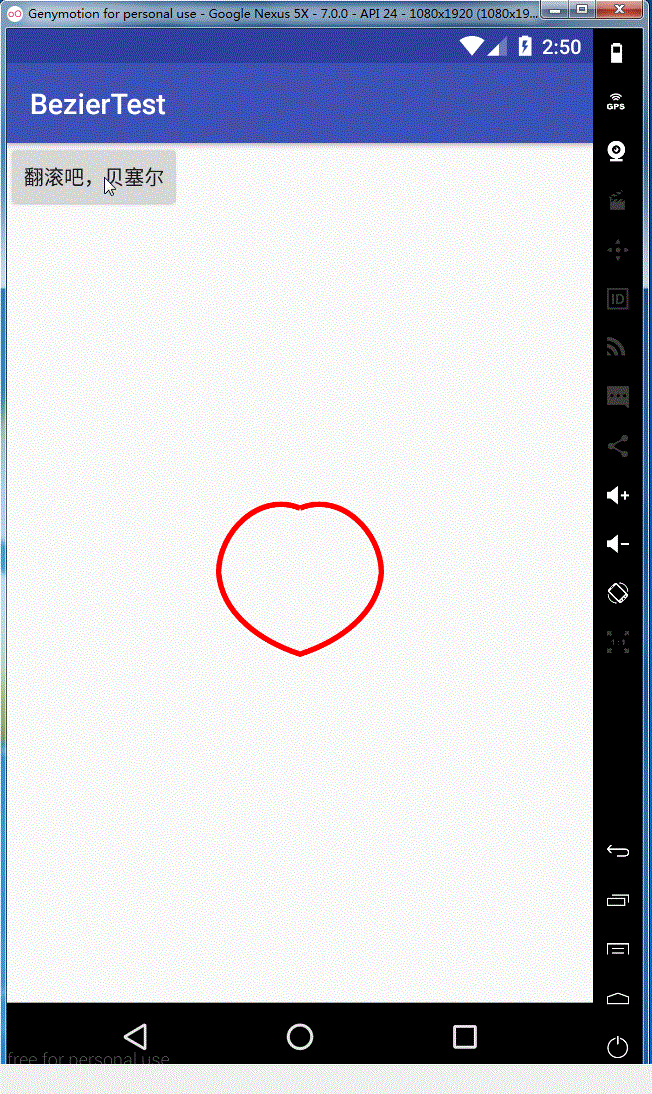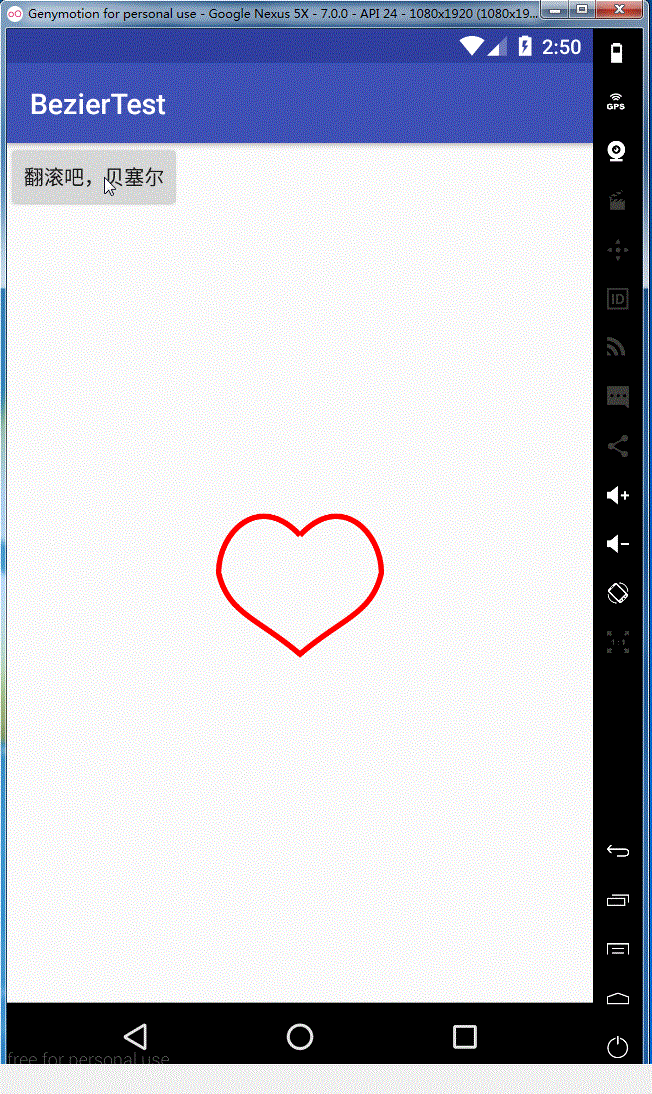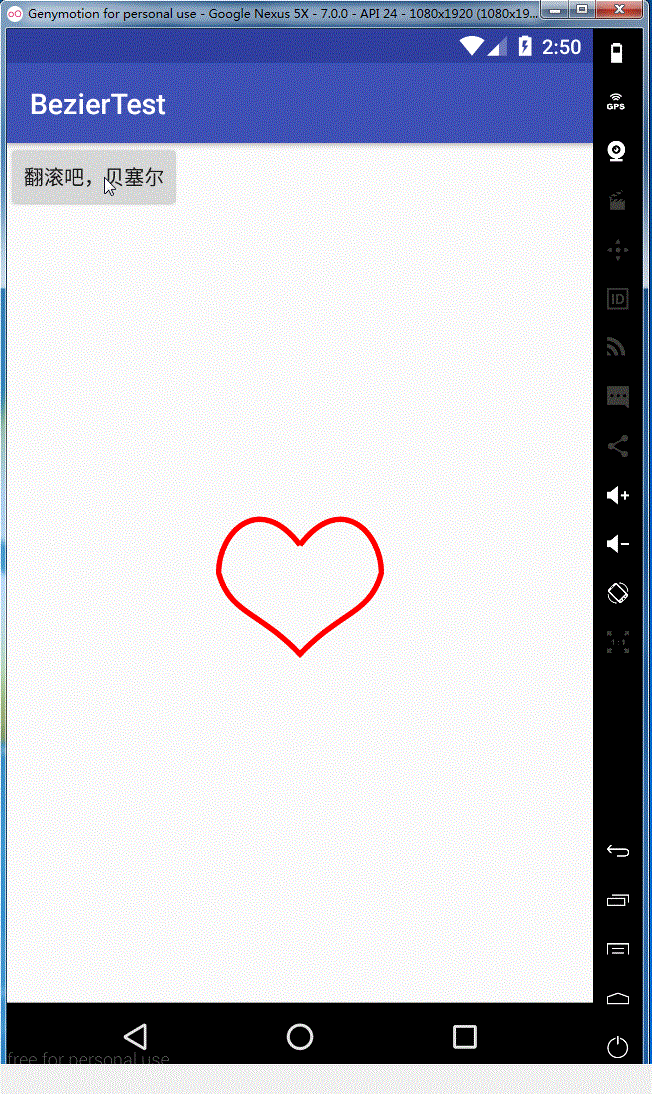
2，思路分析

　　我们知道首先我们的view是一个圆，这里的圆其实是由四块三阶贝塞尔曲线组成的，左上、右上、左下、右下这四块贝塞尔曲线组成，那么让我们来开始吧

• 准备阶段

　　创建一个类MyViewCircle继承自View，重写构造方法，重写onDraw（）方法

public class MyViewCircle extends View {
    public MyViewCircle(Context context) {
        this(context, null);
    }

    public MyViewCircle(Context context, @Nullable AttributeSet attrs) {
        this(context, attrs, 0);
    }

    public MyViewCircle(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
    }
    @Override
    protected void onDraw(Canvas canvas) {

    }
}

• 绘制X、Y轴

　　由于我们的view是展示在屏幕的正中央的，为了我们以后标识点方便，这里我们以屏幕的正中心为（0，0）坐标绘制出来

　　在onSizeChange（）方法中获得mCenterX、mCenterY的坐标，绘制X，Y轴，代码如下：

 private int mCenterX;
 private int mCenterY;
 private Paint mPaint;
//省略代码.........................
     //初始化画笔
        mPaint = new Paint();
        mPaint.setColor(Color.BLACK);
        mPaint.setStrokeWidth(3);
        mPaint.setStyle(Paint.Style.FILL);
        mPaint.setAntiAlias(true);

    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);

        //初始化坐标系
        mCenterX = getWidth() / 2;
        mCenterY = getHeight() / 2;
}

    @Override
    protected void onDraw(Canvas canvas) {
     canvas.save();
        //绘制x，y轴坐标系
        canvas.drawLine(mCenterX, 0, mCenterX, getHeight(), mPaint);
        canvas.drawLine(0, mCenterY, getWidth(), mCenterY, mPaint);

        canvas.restore();
}

　运行效果如下：

　

• 从三阶贝塞尔曲线得到半圆的效果

　　我们上一篇简单的介绍了下三阶贝塞尔，当我们的两个控制点距离数据点为一下坐标时我们绘制出来的曲线是类似于四分之一圆弧的，效果图如下：

　　关于怎么计算出这两个控制点相对于数据点的相对坐标的，这是一个难点，不过还好，在stackoverflow上有人计算出来了，这是链接，我们可以得出一个常量0.552284749831，即相对于原点坐标，半径是mCircleRadius我们的坐标的0.55228倍，这里我为了方便，直接取了0.5，所以这就解释了为什么我们效果图中的圆有点瘪（保持微笑）

• 绘制数据点

　　这里我们四个数据点分别是的是半径为mCircleRadius，圆心坐标为（mCenterX，mCenterY）的圆与我们X、Y轴的焦点，绘制代码如下：

    private Paint mPaintCircle;
    private Paint mPaintPoint;
    private int mCircleRadius;
    private List<PointF> mPointDatas; //放置四个数据点的集合
    private List<PointF> mPointControlls;//方式8个控制点的集合

    //省略代码.....
    //初始化数据
        mPaintCircle = new Paint();
        mPaintCircle.setColor(Color.RED);
        mPaintCircle.setStrokeWidth(10);
        mPaintCircle.setStyle(Paint.Style.STROKE);
        mPaintCircle.setAntiAlias(true);

        mPaintPoint = new Paint();
        mPaintPoint.setColor(Color.BLACK);
        mPaintPoint.setStrokeWidth(5);
        mPaintPoint.setStyle(Paint.Style.FILL);
        mPaintPoint.setAntiAlias(true);

        mCircleRadius = 150;

    //在onSizeChange方法中初始化四个数据点
    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);

        //初始化坐标系
        mCenterX = getWidth() / 2;
        mCenterY = getHeight() / 2;

        mPointDatas = new ArrayList<>();
        mPointControlls = new ArrayList<>();

        mPointDatas.add(new PointF(mCenterX, mCenterY - mCircleRadius));
        mPointDatas.add(new PointF(mCenterX + mCircleRadius, mCenterY));
        mPointDatas.add(new PointF(mCenterX, mCenterY + mCircleRadius));
        mPointDatas.add(new PointF(mCenterX - mCircleRadius, mCenterY));
    }
    //在onDraw方法中绘制数据点
    @Override
    protected void onDraw(Canvas canvas) {
        //绘制x，y轴坐标系
        canvas.drawLine(mCenterX, 0, mCenterX, getHeight(), mPaint);
        canvas.drawLine(0, mCenterY, getWidth(), mCenterY, mPaint);
        //绘制数据点
        for (int i = 0; i < mPointDatas.size(); i++) {
            canvas.drawPoint(mPointDatas.get(i).x, mPointDatas.get(i).y, mPaintPoint);
        }
    }

　　效果图如下：

• 绘制控制点

　　由我们上面的的到的常量0.552284749831，这里使用的是0.5，所以，代码如下

 @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);

        //初始化坐标系
        mCenterX = getWidth() / 2;
        mCenterY = getHeight() / 2;

        mPointDatas = new ArrayList<>();
        mPointControlls = new ArrayList<>();

        mPointDatas.add(new PointF(mCenterX, mCenterY - mCircleRadius));
        mPointDatas.add(new PointF(mCenterX + mCircleRadius, mCenterY));
        mPointDatas.add(new PointF(mCenterX, mCenterY + mCircleRadius));
        mPointDatas.add(new PointF(mCenterX - mCircleRadius, mCenterY));

        mPointControlls.add(new PointF(mCenterX + mCircleRadius / 2, mCenterY - mCircleRadius));
        mPointControlls.add(new PointF(mCenterX + mCircleRadius, mCenterY - mCircleRadius / 2));

        mPointControlls.add(new PointF(mCenterX + mCircleRadius, mCenterY + mCircleRadius / 2));
        mPointControlls.add(new PointF(mCenterX + mCircleRadius / 2, mCenterY + mCircleRadius));

        mPointControlls.add(new PointF(mCenterX - mCircleRadius / 2, mCenterY + mCircleRadius));
        mPointControlls.add(new PointF(mCenterX - mCircleRadius, mCenterY + mCircleRadius / 2));

        mPointControlls.add(new PointF(mCenterX - mCircleRadius, mCenterY - mCircleRadius / 2));
        mPointControlls.add(new PointF(mCenterX - mCircleRadius / 2, mCenterY - mCircleRadius));
    }

  //在onDraw方法中添加控制点的绘制
@Override
    protected void onDraw(Canvas canvas) {
     //绘制x，y轴坐标系
        canvas.drawLine(mCenterX, 0, mCenterX, getHeight(), mPaint);
        canvas.drawLine(0, mCenterY, getWidth(), mCenterY, mPaint);
        //绘制数据点
        canvas.save();
        for (int i = 0; i < mPointDatas.size(); i++) {
            canvas.drawPoint(mPointDatas.get(i).x, mPointDatas.get(i).y, mPaintPoint);
        }
        //绘制控制点
        for (int i = 0; i < mPointControlls.size(); i++) {
            canvas.drawPoint(mPointControlls.get(i).x, mPointControlls.get(i).y, mPaintPoint);
        }
    }

　　绘制后效果图如下：

• 绘制三阶贝塞尔曲线

　　先来绘制右上角四分之一圆弧的贝塞尔曲线看看效果，在onDraw中调用如下代码：

    //利用三阶贝塞尔曲线实现画圆
        Path path = new Path();
        path.moveTo(mPointDatas.get(0).x, mPointDatas.get(0).y);
path.cubicTo(mPointControlls.get(0).x, mPointControlls.get(0).y, mPointControlls.get(1).x, mPointControlls.get(1).y, mPointDatas.get(1)x, mPointDatas.get(1).y);

    //绘制
    canvas.drawPath(path, mPaintCircle);

　 看一下效果：

　　看到了吧  ，效果可以吧，然后我们继续来把后面三条弧线绘制玩，代码如下：

//利用三阶贝塞尔曲线实现画圆
        Path path = new Path();
        path.moveTo(mPointDatas.get(0).x, mPointDatas.get(0).y);
        for (int i = 0; i < mPointDatas.size(); i++) {
            if (i == mPointDatas.size() - 1) {
                path.cubicTo(mPointControlls.get(2 * i).x, mPointControlls.get(2 * i).y, mPointControlls.get(2 * i + 1).x, mPointControlls.get(2 * i + 1).y, mPointDatas.get(0).x, mPointDatas.get(0).y);

            } else {
                path.cubicTo(mPointControlls.get(2 * i).x, mPointControlls.get(2 * i).y, mPointControlls.get(2 * i + 1).x, mPointControlls.get(2 * i + 1).y, mPointDatas.get(i + 1).x, mPointDatas.get(i + 1).y);
            }

        }
        canvas.drawPath(path, mPaintCircle);

　　效果如下：

• 改变数据点和控制点，重绘制view

　　这一步最关键，先来看看我们下面的动画效果

　　　可以看到我们上面动画实现的效果移动有五个点变了：一个Y正轴上数据点改变，四个Y负轴控制点改变了，ok，知道了这些了我们基本上知道了怎么实现了，代码如下：

    private int mDuration = 1000; //动画总时间
    private int mCurrTime = 0;  //当前已进行时间
    private int mCount = 100;//将总时间划分多少块
    private float mPiece = mDuration / mCount; //每一块的时间 ；

    //在onDraw（）方法中动态的刷新view,有人肯定会问，120,80之类的怎么的出来的，我只能说调出来的好嘛（手动微笑），代码如下：
    //动态改变数据点和辅助点
           mCurrTime += mPiece;
           if (mCurrTime < mDuration) {
               mPointDatas.get(0).y += 120 / mCount;
               mPointControlls.get(2).x -= 20.0 / mCount;

               mPointControlls.get(3).y -= 80.0 / mCount;
               mPointControlls.get(4).y -= 80.0 / mCount;
               mPointControlls.get(5).x += 20.0 / mCount;

               postInvalidateDelayed((long) mPiece);
           }

　　ok，这样我们基本上全部完成了，看一下效果

　　ok,这样我们就实现这个效果了，有没有很简单，有需要源码的同学可以在我的Github下载，明天继续，See You Next Time！！！