MOD - Power Modulo Inverted(SPOJ3105) + Clever Y(POJ3243) + Hard Equation (Gym 101853G ) + EXBSGS

思路：

　　前两题题面相同，代码也相同，就只贴一题的题面了。这三题的意思都是求A^X==B(mod P），P可以不是素数，EXBSGS板子题。

SPOJ3105题目链接：https://www.spoj.com/problems/MOD/

POJ3243题目链接:http://poj.org/problem?id=3243

题目:

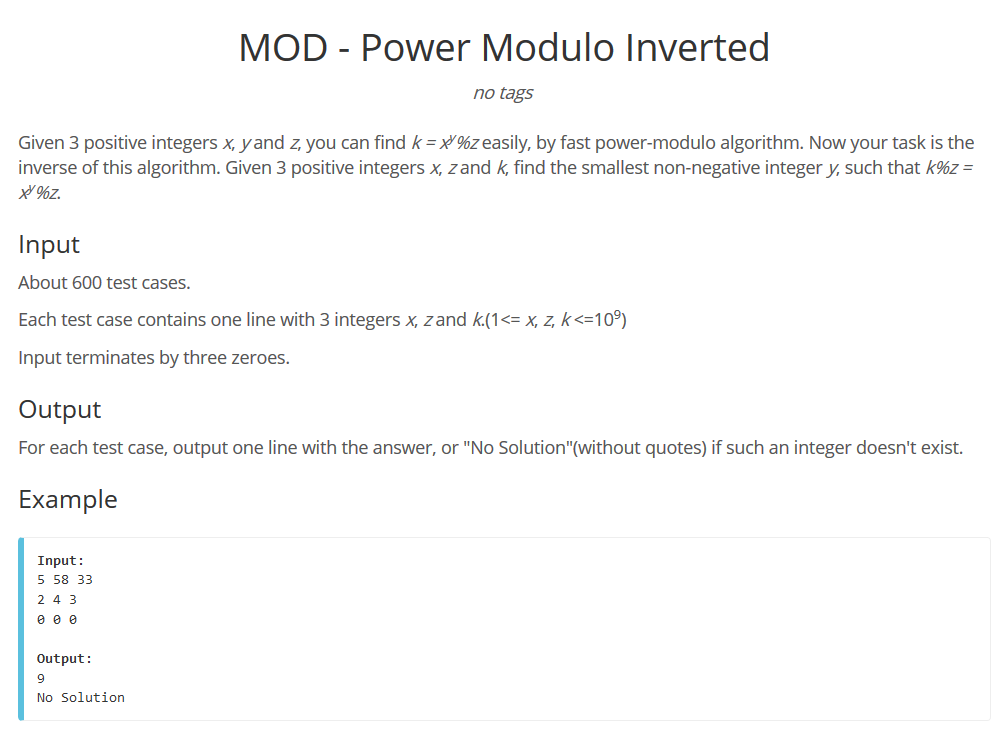
代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #include <unordered_map>
 using namespace std;

 typedef long long LL;
 typedef pair<LL, LL> pLL;
 typedef pair<LL, int> pli;
 typedef pair<int, LL> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long uLL;

 #define lson i<<1
 #define rson i<<1|1
 #define lowbit(x) x&(-x)
 #define bug printf("*********\n");
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define FIN freopen("D://code//in.txt", "r", stdin);
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = 1e9 + ;
 const int maxn = 1e6 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const LL INF = 0x3f3f3f3f3f3f3f3f;

 int x, z, k;
 unordered_map<LL, int> mp;

 int Mod_Pow(int x, int n, int mod) {
     int res = ;
     while(n) {
         if(n & ) res = (LL)res * x % mod;
         x = (LL)x * x % mod;
         n >>= ;
     }
     return res;
 }

 int gcd(int  a, int b) {
     return b ==  ? a : gcd(b, a % b);
 }

 int EXBSGS(int A, int B, int C) {
     A %= C, B %= C;
     if(B == ) return ;
     int cnt = ;
     LL t = ;
     for(int g = gcd(A, C); g != ; g = gcd(A, C)) {
         if(B % g) return -;
         C /= g, B /= g, t = t * A / g % C;
         cnt++;
         if(B == t) return cnt;
     }
     mp.clear();
     int m = ceil(sqrt(1.0*C));
     LL base = B;
     for(int i = ; i < m; i++) {
         mp[base] = i;
         base = base * A % C;
     }
     base = Mod_Pow(A, m, C);
     LL nw = t;
     for(int i = ; i <= m; i++) {
         nw = nw * base % C;
         if(mp.count(nw)) {
             return i * m - mp[nw] + cnt;
         }
     }
     return -;
 }

 int main() {
     //FIN;
     while(~scanf("%d%d%d", &x, &z, &k)) {
         if(x ==  && z ==  && k == ) break;
         int ans = EXBSGS(x, k, z);
         if(ans == -) printf("No Solution\n");
         else printf("%d\n", ans);
     }
     return ;
 }

Gym 101853G题目链接：http://codeforces.com/gym/101853/problem/G

代码实现如下：

 #include <set>
 #include <map>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <bitset>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstdlib>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 #include <unordered_map>
 using namespace std;

 typedef long long LL;
 typedef pair<LL, LL> pLL;
 typedef pair<LL, int> pli;
 typedef pair<int, LL> pil;;
 typedef pair<int, int> pii;
 typedef unsigned long long uLL;

 #define lson i<<1
 #define rson i<<1|1
 #define lowbit(x) x&(-x)
 #define bug printf("*********\n");
 #define debug(x) cout<<"["<<x<<"]" <<endl;
 #define FIN freopen("D://code//in.txt", "r", stdin);
 #define IO ios::sync_with_stdio(false),cin.tie(0);

 const double eps = 1e-;
 const int mod = 1e9 + ;
 const int maxn = 1e6 + ;
 const double pi = acos(-);
 const int inf = 0x3f3f3f3f;
 const LL INF = 0x3f3f3f3f3f3f3f3f;

 int t, a, b, m;
 unordered_map<LL, int> mp;

 LL Mod_Pow(LL x, LL n, LL mod) {
     LL res = ;
     while(n) {
         if(n & ) res = res * x % mod;
         x = x * x % mod;
         n >>= ;
     }
     return res;
 }

 int gcd(int a, int b) {
     return b ==  ? a : gcd(b, a % b);
 }

 LL EXBSGS(int A, int B, int C) {
     A %= C, B %= C;
     if(B == ) return ;
     int cnt = ;
     LL t = ;
     for(int g = gcd(A, C); g != ; g = gcd(A, C)) {
         if(B % g) return -;
         C /= g, B /= g;
         t = t * A / g % C;
         cnt++;
         if(B == t) return cnt;
     }
     mp.clear();
     int m = ceil(sqrt(1.0 * C));
     LL base = B;
     for(int i = ; i < m; i++) {
        mp[base] = i;
        base = base * A % C;
     }
     base = Mod_Pow(A, m, C);
     LL nw = t;
     for(int i = ; i <= m + ; i++) {
         nw = base * nw % C;
         if(mp.count(nw)) {
             return i * m - mp[nw] + cnt;
         }
     }
     return -;
 }

 int main() {
     scanf("%d", &t);
     while(t--) {
         scanf("%d%d%d", &a, &b, &m);
         LL ans = EXBSGS(a, b, m);
         printf("%lld\n", ans);
     }
     return ;
 }