1135 Is It A Red-Black Tree

题意：给出k个二叉搜索树的前序序列，判断该树是否为红黑树。

红黑树的定义：

1. 结点的颜色非红即黑
2. 根结点的颜色必须是黑色
3. 每个叶子结点（指的是空结点，图中并没有画出来）都是黑色的
4. 如果某个结点为红色，则它的孩子节点必须是黑色的。（表明从每个叶子到根的所有路径上不能有两个连续的红色节点。）
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。（所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。）

思路：

红黑树的判断：

1. 根结点是否为黑色。
2. 每条路径的黑色节点相等。统计出一条路径的黑色节点的个数，然后与其他路径黑色节点个数进行比较。
3. 不存在连续的红色节点，判断红色节点的孩子节点是否为红色。

代码：

#include <cstdio>
#include <algorithm>
using namespace std;
#define BLACK 1
#define RED 0

struct Node{
    int val;
    int color;
    Node *lchild,*rchild;
    Node(int v){
        val=v>?v:-v;
        color=v>?BLACK:RED;
        lchild=rchild=nullptr;
    }
};

void insert(Node* &root,int val)
{
    if(root==nullptr){
        root=new Node(val);
        return;
    }
    if(abs(val)<root->val) insert(root->lchild,val);
    else insert(root->rchild,val);
}

//深度遍历，计算黑色结点的个数以及判断是否会出现连续两个红色结点
;
bool flag=true;
void dfs(Node* root,int cnt)
{
    if(root==nullptr){
        if(cnt!=totalBlackCnt) flag=false;
        return;
    }
    if(root->color==BLACK) cnt++;
    else{
        if(root->lchild && root->lchild->color==RED) flag=false;
        if(root->rchild && root->rchild->color==RED) flag=false;
    }
    //printf("val:%d color:%d cnt:%d\n",root->val,root->color,cnt);
    dfs(root->lchild,cnt);
    dfs(root->rchild,cnt);
}

int main()
{　　 int k,n,val;
    scanf("%d",&k);
    while(k--){
        scanf("%d",&n);
        Node* root=nullptr;
        ;i<n;i++){
            scanf("%d",&val);
            insert(root,val);
        }
        if(root->color==RED){
            printf("No\n");
            continue;
        }
        totalBlackCnt=;//记录从根结点到任意一个叶结点的简单路径上黑色结点的个数
        //此处计算最左端的路径
        Node* p=root;
        while(p){
            if(p->color==BLACK) totalBlackCnt++;
            p=p->lchild;
        }
        flag=true;//初始化
        dfs(root,);
        printf("%s\n",flag?"Yes":"No");
    }
    ;
}

【疑问】按照我自己一开始的想法，dfs()函数我是这么写的，然而这么写会有两个测试点通不过！

void dfs(Node* root,int cnt)
{
    if(root==nullptr) return;
    if(root->color==BLACK) cnt++;
    else{
        if(root->lchild && root->lchild->color==RED) flag=false;
        if(root->rchild && root->rchild->color==RED) flag=false;
    }
    if(root->lchild==nullptr && root->rchild==nullptr){
        if(cnt!=totalBlackCnt) flag=false;
    }
    //printf("val:%d color:%d cnt:%d\n",root->val,root->color,cnt);
    dfs(root->lchild,cnt);
    dfs(root->rchild,cnt);
}

【分析】事实上，之所以会这么写，是因为对红黑树的性质(3)还没有真正理解。一开始，对题目给出的这个条件就没搞明白，看了《算法导论》，它上面是这么写的：

树中的每个结点包含5个属性：color，key，left，right，parent。如果一个孩子没有子结点或父结点，则该结点相应指针属性的值为NULL。我们可以把这些NULL视为指向二叉搜索树的叶结点（外部结点）的指针，而把带关键字的结点视为树的内部结点。

因此，对性质(5)“从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点”的真正理解是——这里的叶子结点是空结点，而不是我认为的“没有孩子的结点”。事实上，我们常常把注意力放在内部结点上，因为它存储了关键字的值，而忽略叶结点。但是基本定义，基本概念不能搞混！比如下面图1中的结点8，请问它是叶节点吗？其实不是，因为它也有左右孩子，只不过它的左右孩子不存关键字，为NULL罢了。类似的思想在判断一棵树是否为完全二叉树中也应用到了。见例题。

按照我错误的写法，程序会认为以下这样的也是红黑树：

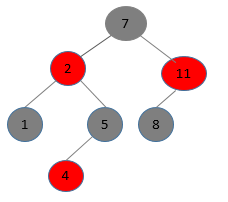
（图1）

然而，这棵树并不是合法的红黑树。根据定义，它真正的形状应该是画成下面这个样子：

（图2）

可以看到，“7->11->null”这条路径中黑色结点的个数与其他路径不等。而按照我错误的写法来理解（即图1），因为结点11不是叶子结点，所以根本不会考虑这条路径上的情况，因此造成错误。

理解了定义之后，修改成如下便可AC，当然，我觉得这种写法不太好，还是上面完整代码中那个版本最佳！

void dfs(Node* root,int cnt)
{
    if(root==nullptr) return;
    if(root->color==BLACK) cnt++;
    else{
        if(root->lchild && root->lchild->color==RED) flag=false;
        if(root->rchild && root->rchild->color==RED) flag=false;
    }
    if(root->lchild==nullptr || root->rchild==nullptr)
        if(cnt!=totalBlackCnt) flag=false;
    }
    dfs(root->lchild,cnt);
    dfs(root->rchild,cnt);
}