【51nod-1315】合法整数集(数位)
【思路】
既然是or操作,将数转化为二进制,数位是1,对应的数组元素+1,再将x转为成二进制,只要查找X为1的位置,将之前存放的数组数字找个最小的输出就可以了。
但是并不是所有的数都要参与or,因为有些数的位数>X,显然这些数是不用删除的,所以不用让这些数加到数组里。还有哪些数呢?当有些数的位数是1,而X对应的位数是0,这些数也是一定不用删除的。综合以上只要满足(x|xx)> x就可以参与or。
【code】
#include <bits/stdc++.h>
using namespace std;
int a[];
int main()
{
int n, m, x, c = , ans = 1e9;
cin>>n>>m;
for(int i=; i<n; i++)
{
scanf("%d", &x);
if((x|m) > m) continue;//
c = ;
while(x)
{
c++;
if(x & ) a[c]++;
x >>= ;
}
}
c = ;
while(m)
{
c++;
if(m & ) ans = min(ans, a[c]);
m >>= ;
}
printf("%d\n", ans);
return ;
}
【51nod-1315】合法整数集(数位)的更多相关文章
- 51Nod 1315 合法整数集
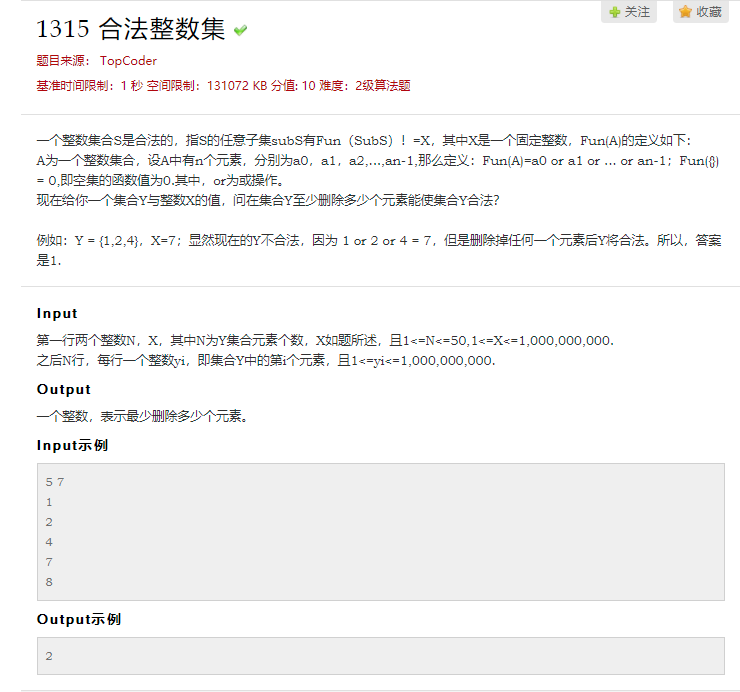
1315 合法整数集 题目来源: TopCoder 基准时间限制:1 秒 空间限制:131072 KB 分值: 10 难度:2级算法题 收藏 关注 一个整数集合S是合法的,指S的任意子集subS有Fu ...
- 疯狂位图之——位图实现12GB无重复大整数集排序
<Programming Pearls>(编程珠玑)第一章讲述了如何用位图排序无重复的数据集,整个思想很简洁,今天实践了下. 一.主要思想 位图排序的思想就是在内存中申请一块连续的空间作为 ...
- 给定一个正整数,实现一个方法求出离该整数最近的大于自身的 换位数 <把一个整数各个数位进行全排列>
"""给定一个正整数,实现一个方法求出离该整数最近的大于自身的 换位数 -> 把一个整数各个数位进行全排列""" # 使用 permu ...
- C/C++ 合法整数与字符
一.C语言中的合法整型 首先C语言中的整型有三种表示方式:十进制.八进制和十六进制.(C语言中没有表示二进制的整型) 十进制: 如 int a = 63; //一个正常的整型 八进制: 如果想用8进制 ...
- 【BZOJ2728】[HNOI2012]与非 并查集+数位DP
[BZOJ2728][HNOI2012]与非 Description Input 输入文件第一行是用空格隔开的四个正整数N,K,L和R,接下来的一行是N个非负整数A1,A2……AN,其含义如上所述. ...
- 51nod 1791 合法括号子段
有一个括号序列,现在要计算一下它有多少非空子段是合法括号序列. 合法括号序列的定义是: 1.空序列是合法括号序列. 2.如果S是合法括号序列,那么(S)是合法括号序列.3.如果A和B都是合法括号序列, ...
- 51Nod 1048 1383 整数分解为2的幂
任何正整数都能分解成2的幂,给定整数N,求N的此类划分方法的数量! 比如N = 7时,共有6种划分方法. 7=1+1+1+1+1+1+1 =1+1+1+1+1+2 =1+1+1+2+2 ...
- BZOJ2728 HNOI2012与非(并查集+数位dp)
容易发现x nand x=not x.并且使用这个性质有x and y=not(x nand y)=(x nand y)nand(x nand y).也就是说nand运算可以作为not和and运算使用 ...
- 51Nod 快速傅里叶变换题集选刷
打开51Nod全部问题页面,在右边题目分类中找到快速傅里叶变换,然后按分值排序,就是本文的题目顺序. 1.大数乘法问题 这个……板子就算了吧. 2.美妙的序列问题 长度为n的排列,且满足从中间任意位置 ...
随机推荐
- 企业级项目把.app文件转成.ipa文件的自动化实现
将MakeIPA.sh添加到项目的根目录下 此脚本针对企业级项目打包,不会编译项目,在打包前确认项目已经编译完成生成了"XXX.app"文件 使用前需要配置该脚本部分路径才能正确打 ...
- 论文笔记:CNN经典结构1(AlexNet,ZFNet,OverFeat,VGG,GoogleNet,ResNet)
前言 本文主要介绍2012-2015年的一些经典CNN结构,从AlexNet,ZFNet,OverFeat到VGG,GoogleNetv1-v4,ResNetv1-v2. 在论文笔记:CNN经典结构2 ...
- matlab基本操作总结
1.clear;//清除工作平台变量2.close all;//关闭打开的图形窗口3.I = imread('C:\Users\dell\Desktop\rice.jpg');//读取图像,存储在I数 ...
- web.xml<context-param>与<init-param>的作用与区别
<context-param>的作用:web.xml的配置中<context-param>配置作用1. 启动一个WEB项目的时候,容器(如:Tomcat)会去读它的配置文件we ...
- c/c++调用dll
1.lib.h 1 #ifndef LIB_H 2 #define LIB_H 3 4 #include <windows.h> 5 #include <iostream> 6 ...
- 20145201李子璇《网络对抗》逆向及Bof基础实践
20145201李子璇<网络对抗>逆向及Bof基础实践 实践目标 本次实践的对象是一个名为pwn1的linux可执行文件. 该程序正常执行流程是:main调用foo函数,foo函数会简单回 ...
- TCP深入详解
TCP三次握手.四次挥手时序图: #TCP协议状态机 1.TCP建立连接时的初始化序列号X.Y可以是写死固定的吗? 如果初始化序列号(缩写为ISN:Inital Sequence Numbe ...
- python使用百度api翻译中英文
python使用百度api翻译中英文 写程序取变量名的时候,常常需要翻译单词,或者将中文翻译成英语.有道词典,必应词典都很好,可是...命令行习惯了还是觉得用在cmd里面调出程序使用起来也许会更爽.于 ...
- 如何使一个openwrt下的软件开机自启动
条件有三: 1.需要在软件包的Makefile中添加宏定义Package/$(package-name)/preinst和Package/$(package-name)/prerm define Pa ...
- 数据结构实习 - Problem N 树的括号表示法
writer:pprp date:20171103 题目描述 先将根结点放入一对圆括号中,然后把它的子树按由左而右的顺序放入括号中,而对子树也采用同样方法处理:同层子树与它的根结点用圆括号括起来,同层 ...
