【Python算法】归纳、递归、归简

归简法(reduction)

　　指的是将某一问题转化成另一个问题，将一个未知问题归简成一个已解决的问题。

归纳法(induction)

　　首先要证明语句在某一基本情况下是成立的，然后证明他可以由一个对象推广到下一个对象（如果对n-1成立，那么它对于n也成立）

递归法(recursion)

　　需要确保函数在遇到基本情况base case时的操作是正确的，并且能将各层递归调用的结果组合成一个有效的解决方法。

归简法：Let’s take an example.

　　假设想从某个数字列表中找出两个最接近但不相等的数

方法一：

from random import randrange
seq = [randrange(10**10) for i in range(100)]
dd = float('inf')
for x in seq:
    for y in seq:
        if x==y : continue
        d = abs(x-y)
        if d < dd:
            xx,yy,dd =x,y,d
print(x,y,dd)

算法一：采用了两层嵌套循环（Two nested loops），这是一个平方级操作。（quadratic）

归简后：

seq.sort()
for i in range(len(seq)-1):
    x,y = seq[i],seq[i+1]
    if x == y :continue
    d = abs(x-y)
    if d < dd:
        xx, yy, dd = x, y, d

先对列表进行排序，而排序通常是一个线性对数级或者Θ（nlgn）级操作，新的运行时间由排序操作主导。

原问题是：找出数列中最接近的两个数，通过对seq进行排序，我们将其归简成 找出以排序序列中最接近的两个数，并不会影响原问题的答案。

将A归简成B类似于，你想解决A，只要你能解决B就行了。

归纳法：Let’s take an example.

　　先提出一个命题或语句P（n），再来证明他对任何自然数n都成立。

　　我们想考察前n个数中的奇数之和，那么其P（n）可能会是以下语句：

　　

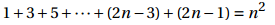
归纳法的思路：

　　建立一条涵盖所有自然数的扫描式的证据链，我们必须要证明如果语句P(n-1)是成立的，那么P(n)也必然成立

　　如果我们能证明其中的隐含关系，P(n-1)→P(n)，该结果就能贯穿于n的所有值，从P(1)开始，用P(1)→P(2)来证明P(2)成立，继续转向P(3)、P(4n)等；

　　关键就是这层隐含关系要成立，然后将该关系进一步推导下去。称之为归纳步骤

　　P(n-1) 假设为：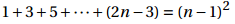

　　拼接到原式 P(n)：

　　

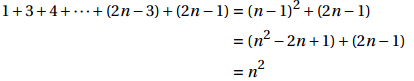
　　最主要一步是假设P(n-1)已经成立。从已知的与n-1相关的信息开始，构建出n相关的情况！

递归法：

　　归纳法证明了递归法的适用性，而递归法则是我们实现归纳法思维的一种简单方式。

　　任何递归函数都可以被重写成相应的迭代操作。（反之亦然）

插入排序法：

　　思路：归纳性假设前n-1个元素已经完成了排序了，现在要将第n个元素插入到正确的位置上！

def insert_sort(seq,n):
    if n == 0 :return
    insert_sort(seq,n-1)
    j = n
    while j>0 and seq[j-1] > seq[j]:
        seq[j-1],seq[j] = seq[j],seq[j-1]
        j -= 1

选择排序法：

　　思路：先找到序列中最大的元素，并将其放在n的位置上，然后继续递归排序剩下的元素！

def select_sort(seq,n):
    if n == 0 : return
    max_j = n
    for i in range(n):
        if seq[i] > seq[max_j]:
            max_j = i
    seq[max_j],seq[n] = seq[n],seq[max_j]
    select_sort(seq,n-1)

寻找最大排列：

　　现在八个人去电影院看电影，他们现在都有了自己的位置，但是他们其中有的满意，有的不满意。他们想做的座位如下图：

　　图中a,b,c,d,e,f,g,h都表示座位，也表示座位上的人，箭头指向他们想坐的座位。

　　

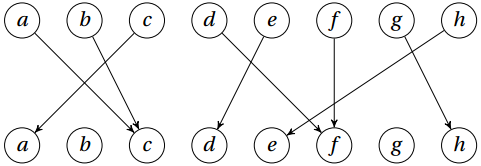
分析如下：

　　1.如果各个人指向的座位不同，那么整个集合本身就是结果了。（大家喜欢的座位各不相同，那还争什么呀，大家交换就是了）

　　2.那么至少要有两个人指向同一个座位（这样问题才有意思，有人争座位！a和b他们有一个肯定不在结果集中！那么要淘汰谁呢？！）

　　3.淘汰那个没有人指向自己座位的人！（比如淘汰a的话，那么接下来c也没地方去了。哎。后果很严重！）

假设：M=[2,2,0,5,3,5,7,4]   #表示他们想去的位置

def naive_max_num(M,A=None):
    if A==None:
        A=set(range(len(M)))
    if len(A) == 1:
        return A
    B = set(M[x] for x in A)
    C = A-B
    if C:
        A.remove(C.pop())
        naive_max_num(M,A)
    return A

时间复杂度：平方级。因为B的生成需要线性时间。

引入计数的思想：

　　为各元素设置一个计数器，我们先淘汰空座位，然后再找到该座位属于者x，我们就只需递减该x指向座位的计数器，并在x的计数器为0时，将编号为x的人和座位一同出局即可。

def max_perm(M):
    n=len(M)
    A = set(range(n))
    counts=[0]*n
    for i in M:
        counts[i] += 1
    Q = [i for i in A if counts[i] == 0]
    while Q:
        i = Q.pop()
        A.remove(i)
        j = M[i]
        counts[j] -= 1
        if counts[j] == 0:
            Q.append(j)
    return A

时间复杂度：线性级

计数排序：( 稳定排序 )

　　如果所操作的元素都是可以被哈希的，可以采用计数排序，（在最坏情况下能达到线性对数级操作）

　　通过引入一个键值函数，我们可以按照自己喜欢的方式进行排序！

from collections import defaultdict
def counting_sort(A,key=lambda x :x):
    B,C=[],defaultdict(list)
    for x in A:
        C[key(x)].append(x)
    for k in range(min(C),max(C)+1):
        B.extend(C[k])
    return B

　　

拓扑排序：

　　对一个有向无环图(Directed Acyclic Graph简称DAG) G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。

　　通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。

　　几乎在所有的项目中，待完成的任务之间通常都会存在着某些依赖关系，这些关系会对它们的执行顺序形成部分约束。

　　对于这种依赖关系，我们通常很容易将其表示成一个有向无环路图（DAG），并将寻找其中依赖顺序的过程（寻找所有沿着特定顺序前进的边与点）成为拓扑排序（topological sorting）

　　

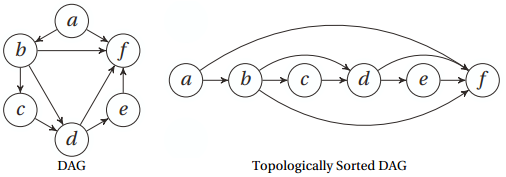
思路：

　　首先移除其中一个节点，然后解决其余n-1个节点的问题。但，这首先要保证移除之后还是一个DAG。就是需要移除那些没有入边的节点。

　　通过计数方式，统计节点入边数！

def topSort(G):
    count = dict((u,0) for u in G)
    for u in G:
        for v in G[u]:
            count[v] += 1
    Q = [u for u in count if count[u]==0]
    S = []
    while Q:
        u = Q.pop()
        S.append(u)
        for u in G[u]:
            count[u] -= 1
            if count[u] == 0:
                Q.append(u)
    return S

if __name__=="__main__":
    G={
        'a':set('bf'),
        'b':set('cdf'),
        'c':set('d'),
        'd':set('ef'),
        'e':set('f'),
        'f':set('')
        }
    seq=topSort(G)
    print(seq)