Madgwick算法详细解读
Madgwick算法详细解读
极品巧克力
前言
接上一篇文章《Google Cardboard的九轴融合算法》。
Madgwick算法是另外一种九轴融合的方法,广泛应用在旋翼飞行器上,效果也蛮不错的。网上已经有很多madgwick算法的源代码了。
本文结合参考文献,按照我自己的理解,把Madgwick算法的来龙去脉讲清楚。
1.加权融合
由于姿态都是相对的,用 来表示水平朝北静止时的物体,
来表示水平朝北静止时的物体, 代表运动后的物体。所以,运动时的物体相对水平朝北静止时的物体的姿态可以用四元数
代表运动后的物体。所以,运动时的物体相对水平朝北静止时的物体的姿态可以用四元数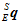 来表示。
来表示。
主要基于Madgwick算法对传感器数据进行融合。Madgwick算法的本质是加权整合t时刻的陀螺仪算出的姿态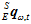 和加速度计磁场计共同算出的姿态
和加速度计磁场计共同算出的姿态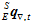 ,从而得到最终的姿态
,从而得到最终的姿态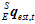 。其加权公式如下。
。其加权公式如下。
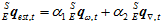
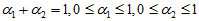
其中,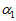 和
和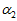 是加权系数,它们是由各自的误差占总体误差的比重所决定的,误差所占的比重越小则加权系数越大。设采样时间间隔为
是加权系数,它们是由各自的误差占总体误差的比重所决定的,误差所占的比重越小则加权系数越大。设采样时间间隔为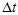 。陀螺仪的单位时间的误差
。陀螺仪的单位时间的误差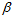 可以通过查陀螺仪的手册得到,一般是一个很小的值,所以陀螺仪的误差为
可以通过查陀螺仪的手册得到,一般是一个很小的值,所以陀螺仪的误差为 。而加速度计磁场计共同算出的姿态的误差是由计算方法决定的,计算方法如梯度下降法、高斯牛顿迭代法、牛顿法、共轭梯度法等,由于采用的方法是梯度下降法,所以其误差为梯度下降法中所选取的步长
。而加速度计磁场计共同算出的姿态的误差是由计算方法决定的,计算方法如梯度下降法、高斯牛顿迭代法、牛顿法、共轭梯度法等,由于采用的方法是梯度下降法,所以其误差为梯度下降法中所选取的步长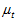 ,步长越长则其计算结果的误差越大。所以,总体误差为
,步长越长则其计算结果的误差越大。所以,总体误差为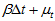 。
。
 是陀螺仪算出的姿态的加权系数。
是陀螺仪算出的姿态的加权系数。
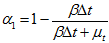
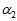 是加速度计磁场计所算出的姿态的加权系数。
是加速度计磁场计所算出的姿态的加权系数。
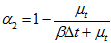
于是,接下来需要得到的是陀螺仪计算出的姿态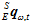 和加速度计磁场计共同算出的姿态
和加速度计磁场计共同算出的姿态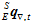 。
。
2.陀螺仪姿态估计
用陀螺仪的数据来计算出姿态 。
。
三轴陀螺仪返回的数据是自身分别绕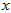 轴、
轴、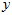 轴、
轴、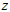 轴的角速度,这三个角速度分别用
轴的角速度,这三个角速度分别用 、
、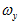 、
、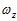 来表示。则陀螺仪返回的数据可以看成实部为零的四元数,用
来表示。则陀螺仪返回的数据可以看成实部为零的四元数,用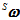 来表示。
来表示。
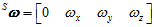
而姿态四元数变化的速度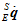 与当前的姿态
与当前的姿态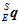 和角速度
和角速度 有关,其计算公式如下。
有关,其计算公式如下。
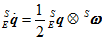
现在已知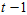 时刻的四元数
时刻的四元数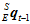 和角速度
和角速度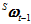 ,以及
,以及 时刻的角速度
时刻的角速度 ,系统采样间隔为
,系统采样间隔为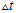 ,求
,求 时刻的四元数
时刻的四元数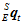 。类似于常微分方程,套用改进的欧拉公式。
。类似于常微分方程,套用改进的欧拉公式。
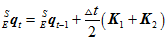

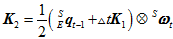
这里用改进的欧拉方法,其实就是近似估计物体四元数在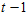 时刻到
时刻到 时刻之间的平均变化速度
时刻之间的平均变化速度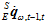 。而在实际过程中,往往并不能得到
。而在实际过程中,往往并不能得到 时刻的准确的四元数,而是一个最优的估计值
时刻的准确的四元数,而是一个最优的估计值 。
。


从而得到,
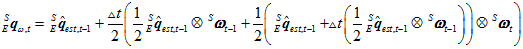
另外,在实际过程中,受传感器特性的影响,陀螺仪、加速度计、磁场计的最大采样速度不一样。系统采样间隔 是为了满足这三个传感器中最低的采样速度,使得能同时采样。而实际上,陀螺仪的采样速度可以比另外两个传感器的速度快很多。所以,如果为了追求更高的精度的话,可以分开采样。假设陀螺仪的采样间隔是
是为了满足这三个传感器中最低的采样速度,使得能同时采样。而实际上,陀螺仪的采样速度可以比另外两个传感器的速度快很多。所以,如果为了追求更高的精度的话,可以分开采样。假设陀螺仪的采样间隔是 ,则可用
,则可用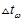 代替上面公式中的
代替上面公式中的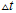 ,用欧拉公式一步一步地往后计算,重复
,用欧拉公式一步一步地往后计算,重复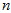 次,直到
次,直到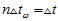 ,就得到了高精度的下一个系统采样时刻的四元数,并且这个四元数与另外两个传感器同步。
,就得到了高精度的下一个系统采样时刻的四元数,并且这个四元数与另外两个传感器同步。
3.加速度计磁场计姿态估计
要用加速度计和磁场计来共同算出姿态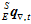 。
。
当物体水平静止朝北时,加速度计的理论输出 和磁场计的理论输出
和磁场计的理论输出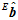 分别如下,都可以看成是实部为0的四元数。
分别如下,都可以看成是实部为0的四元数。
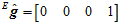

将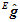 和
和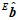 的虚部组成一个向量
的虚部组成一个向量 。
。
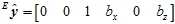
而在物体运动之后,在 时刻,上述的两个传感器的数据都发生了变化。加速度传感器的归一化后的数据
时刻,上述的两个传感器的数据都发生了变化。加速度传感器的归一化后的数据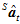 和磁场计的归一化后的数据
和磁场计的归一化后的数据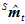 分别如下,都可以看成是实部为0的四元数。
分别如下,都可以看成是实部为0的四元数。
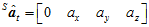
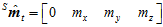
将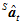 和
和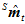 的虚部组成一个向量
的虚部组成一个向量 。
。
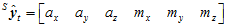
设这个时候的物体的姿态为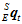 ,则按照四元数的矢量旋转性质可建立
,则按照四元数的矢量旋转性质可建立 和
和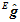 的关系,
的关系, 和
和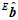 的关系,得到如下方程。
的关系,得到如下方程。
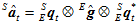
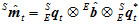
分别用旋转矩阵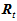 表示。
表示。

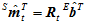
将 组合成一个新的矩阵
组合成一个新的矩阵 。
。

于是,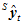 和
和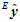 的关系,用矩阵
的关系,用矩阵 来表示。
来表示。
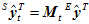
在上式中, 和
和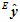 是已知的,所以可以由上式再反过来去求出
是已知的,所以可以由上式再反过来去求出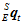 。即求出一个
。即求出一个 ,
,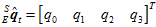 ,由此转换成
,由此转换成 ,使得误差平方和
,使得误差平方和 最小。
最小。
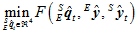
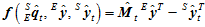
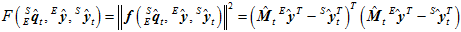
其中,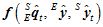 是一个多元向量函数,而求多元向量函数的极值问题,在计算机中一般采用数值解法,如梯度下降法、高斯牛顿迭代法、牛顿法、共轭梯度法等。采用梯度下降法。
是一个多元向量函数,而求多元向量函数的极值问题,在计算机中一般采用数值解法,如梯度下降法、高斯牛顿迭代法、牛顿法、共轭梯度法等。采用梯度下降法。
设 的初值为
的初值为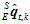 ,为4行1列的矩阵,则误差平方和为
,为4行1列的矩阵,则误差平方和为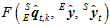 。假设这个初值四元数
。假设这个初值四元数 需要修正的量为
需要修正的量为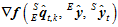 ,则修正后的误差平方和为
,则修正后的误差平方和为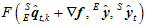 。
。
由泰勒公式展开可得,
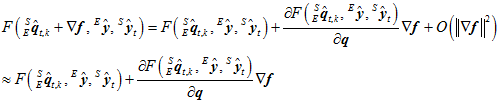
其中,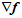 为4行1列的矩阵。
为4行1列的矩阵。 为1行4列的矩阵,如下所示。
为1行4列的矩阵,如下所示。
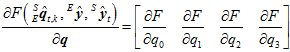
则梯度大小如下。

其中,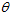 为向量
为向量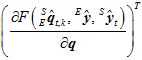 与单位向量
与单位向量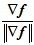 的夹角。所以,当
的夹角。所以,当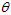 为
为 时,上式有最小值,即误差平方和降得最快。
时,上式有最小值,即误差平方和降得最快。
若要让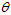 为
为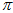 ,则要让上述两个向量的方向相同,即
,则要让上述两个向量的方向相同,即 要满足如下的等式关系。
要满足如下的等式关系。
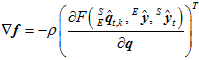
其中,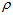 为一个大于零的比例系数。上式中的
为一个大于零的比例系数。上式中的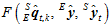 关于四元数
关于四元数 的偏导,可以计算如下。
的偏导,可以计算如下。
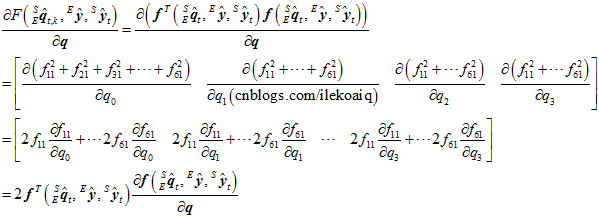
其中,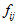 代表
代表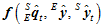 中第
中第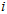 行第
行第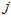 列的元素。
列的元素。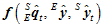 的表达式如下。
的表达式如下。

而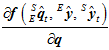 就是
就是 关于四元数的偏导,即其雅克比矩阵。
关于四元数的偏导,即其雅克比矩阵。
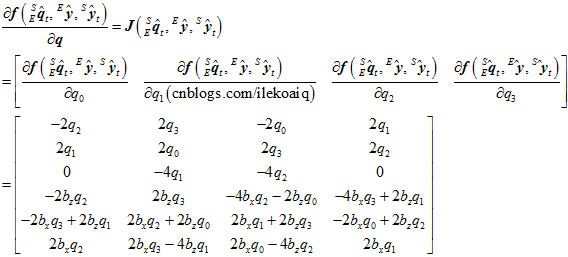
所以, 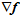 的计算可以转换成,
的计算可以转换成,
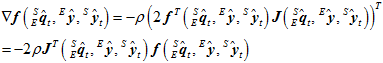
进行归一化,除以其2范数,得到梯度的方向,表达式如下。

然后再乘以步长 ,就得到了各个自变量要改变的值。各个自变量现有的值加上要修正的量,得到了新的对
,就得到了各个自变量要改变的值。各个自变量现有的值加上要修正的量,得到了新的对 的估计,如下面公式所示。
的估计,如下面公式所示。
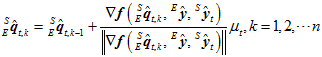
梯度下降法是一个不停迭代的过程。用上一时刻的姿态 作为初值
作为初值 ,即已知上一次的估计
,即已知上一次的估计 ,代入上述公式中。重复之前的步骤,进行多次迭代,直到
,代入上述公式中。重复之前的步骤,进行多次迭代,直到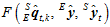 小于某一阈值,此时,
小于某一阈值,此时,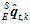 为
为 的最佳估计值。或者经过多次迭代,直到满足
的最佳估计值。或者经过多次迭代,直到满足 ,此时,
,此时,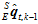 为
为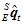 的最佳估计值。
的最佳估计值。
步长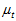 需要通过人为来设定。步长
需要通过人为来设定。步长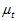 越小,则最终结果的精度越高,但迭代的次数也会越多。步长
越小,则最终结果的精度越高,但迭代的次数也会越多。步长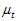 越大,则最终结果的误差越大,但迭代的次数也会越少。
越大,则最终结果的误差越大,但迭代的次数也会越少。
用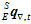 来表示最终通过梯度下降法融合加速度计和磁场计来共同估计出的姿态,即上述的最佳估计值。
来表示最终通过梯度下降法融合加速度计和磁场计来共同估计出的姿态,即上述的最佳估计值。
4.算法简化
由前面的陀螺仪积分的结果和加速度计磁场计优化的结果加权,就可以得到高精度的融合结果。
但是,在实际工程中,需要权衡计算精度和计算速度。在梯度下降法的迭代过程,虽然之前的方法可以使得结果的精度更高,但是也增加了计算量。在实际工程中,如果要追求速度的话,可以对这些地方进行简化。
在 时刻到
时刻到 时刻之间的变化速度
时刻之间的变化速度 可以用如下公式近似。
可以用如下公式近似。
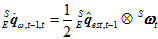
所以, 的计算公式也可简化如下。
的计算公式也可简化如下。
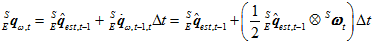
而梯度下降法的迭代过程,也可以只用一步来简化,即认为一步就可以近似达到最佳估计值。那就是要设置步长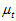 ,使得迭代一次就能最接近最佳估计值。
,使得迭代一次就能最接近最佳估计值。

其中,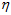 是一个根据实际情况调节的量,用来弥补加速度计和磁场计的测量误差。上式中的
是一个根据实际情况调节的量,用来弥补加速度计和磁场计的测量误差。上式中的 ,如果要追求更高的精度,仍可使用之前的计算公式。如果追求速度,采用简化公式,所以,简化后的
,如果要追求更高的精度,仍可使用之前的计算公式。如果追求速度,采用简化公式,所以,简化后的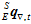 计算公式如下。
计算公式如下。
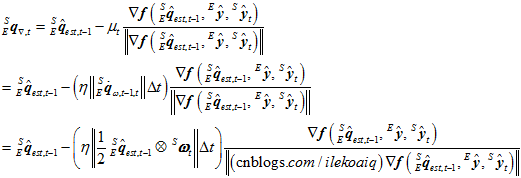
最终,将 和加权
和加权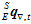 融合,得到最佳的姿态估计。
融合,得到最佳的姿态估计。
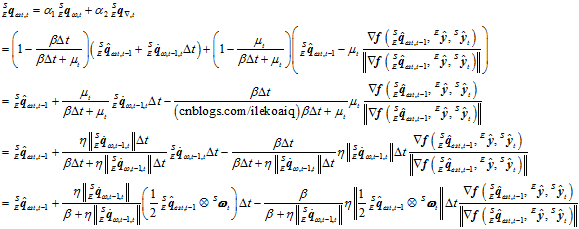
其中, 。在上式的分母中,由于
。在上式的分母中,由于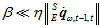 ,所以
,所以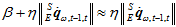 ,于是上式可以进一步简化成,
,于是上式可以进一步简化成,
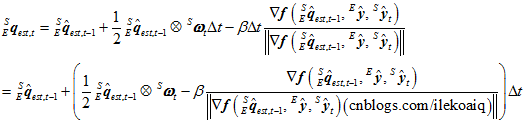
相当于是陀螺仪计算出来的四元数变化速度与加速度计磁场计计算出来的变化速度加权整合,前者的权重是1,后者的权重是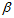 。
。
然后,对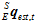 进行归一化,得到
进行归一化,得到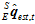 。
。
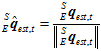
5.磁场计修正
由于物体是在不停地运动之中的,物体周围的磁场容易受环境变化影响,即水平静止朝北时的磁场计理论输出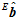 可能会由于环境的变化而发生改变。而水平静止朝北时的加速度计理论输出
可能会由于环境的变化而发生改变。而水平静止朝北时的加速度计理论输出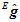 则几乎不受环境影响。所以,为了能得到一个更加精确的姿态估计,
则几乎不受环境影响。所以,为了能得到一个更加精确的姿态估计, 不能像
不能像 那样采用一个固定值,而需要实时修正。
那样采用一个固定值,而需要实时修正。
在传感器刚开始运行的时候,即第一帧的时候,传感器可能处于任意一种姿态,几乎不会是水平静止朝北的,所以磁场计的输出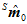 几乎不会是
几乎不会是 。所以,
。所以,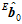 是未知的。而这时候,可以用加速度计的输出
是未知的。而这时候,可以用加速度计的输出 来计算出物体的姿态。
来计算出物体的姿态。
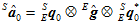
用旋转矩阵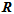 表示。
表示。
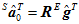
在上式中,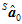 和
和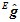 是已知的,所以可以由上式再反过来去求出第一帧的姿态
是已知的,所以可以由上式再反过来去求出第一帧的姿态 。即求出一个
。即求出一个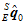 ,转换成
,转换成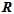 ,使得
,使得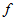 最小。
最小。

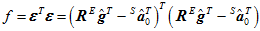
用高斯牛顿迭代法来寻找这个最佳的四元数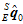 。先计算其雅克比矩阵,
。先计算其雅克比矩阵,

假设当前四元数各个元素的误差为4行1列的矩阵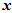 ,则
,则 。用最小二乘法来计算出
。用最小二乘法来计算出 。
。

所以,现有的四元数的值减去误差,得到新的四元数。

 的初值可以设为如下。
的初值可以设为如下。
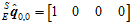
重复上述公式,迭代多次,直到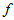 达到最小值。
达到最小值。
于是就得到加速度计估计出的第一帧的姿态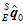 。
。
所以,根据四元数的坐标系旋转性质,可以把坐标系转到水平的位置上,但并不能保证朝北。对于向量来讲,坐标系逆着四元数转回去,就相当于是向量顺着四元数继续转,得到在这个水平坐标系中的磁场的向量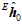 。
。
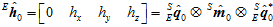
其中, 和
和 是
是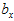 在这个坐标系中的
在这个坐标系中的 轴和
轴和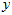 轴上的分量,所以可以得到
轴上的分量,所以可以得到 。
。
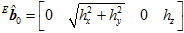
以上是第一帧的时候得到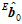 的方法。
的方法。
再将加速度计估计出来的姿态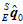 作为初值,将
作为初值,将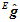 、
、 、
、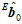 、
、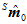 代入到之前公式中,用梯度下降法迭代,得到高精度的第一帧的姿态
代入到之前公式中,用梯度下降法迭代,得到高精度的第一帧的姿态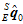 。
。
当物体发生运动之后,由于周围环境的影响,每一帧都要对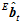 进行修正。假设已经用之前的方法得到上一帧的最佳的姿态估计
进行修正。假设已经用之前的方法得到上一帧的最佳的姿态估计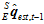 ,则这一帧的
,则这一帧的 计算如下。
计算如下。


6.求赞赏
您觉得,本文值多少?

7.参考文献
- Madgwick S O H, Harrison A J L, Vaidyanathan R. Estimation of IMU and MARG orientation using a gradient descent algorithm[C]//Rehabilitation Robotics (ICORR), 2011 IEEE International Conference on. IEEE, 2011: 1-7.
Madgwick算法详细解读的更多相关文章
- 和textrank4ZH代码一模一样的算法详细解读
前不久做了有关自动文摘的学习,采用方法是TextRank算法,整理和大家分享. 一. 关于自动文摘 利用计算机将大量的文本进行处理,产生简洁.精炼内容的过程就是文本摘要,人们可通过阅读摘要来把握文本主 ...
- A*寻路算法详细解读
文章目录 A*算法描述 简化搜索区域 概述算法步骤 进一步解释 具体寻路过程 模拟需要更新F值的情况 Lua代码实现 在学习A*算法之前,很好奇的是A*为什么叫做A*.在知乎上找到一个回答,大致意思是 ...
- 相机IMU融合四部曲(一):D-LG-EKF详细解读
相机IMU融合四部曲(一):D-LG-EKF详细解读 极品巧克力 前言 前两篇文章<Google Cardbord的九轴融合算法>,<Madgwick算法详细解读>,讨论的都是 ...
- MemCache超详细解读
MemCache是什么 MemCache是一个自由.源码开放.高性能.分布式的分布式内存对象缓存系统,用于动态Web应用以减轻数据库的负载.它通过在内存中缓存数据和对象来减少读取数据库的次数,从而提高 ...
- MemCache超详细解读 图
http://www.cnblogs.com/xrq730/p/4948707.html MemCache是什么 MemCache是一个自由.源码开放.高性能.分布式的分布式内存对象缓存系统,用于 ...
- MemCache详细解读
MemCache是什么 MemCache是一个自由.源码开放.高性能.分布式的分布式内存对象缓存系统,用于动态Web应用以减轻数据库的负载.它通过在内存中缓存数据和对象来减少读取数据库的次数,从而提高 ...
- 为你详细解读HTTP请求头的具体含意
当我们打开一个网页时,浏览器要向网站服务器发送一个HTTP请求头,然后网站服务器根据HTTP请求头的内容生成当次请求的内容发送给浏览器.你明白HTTP请求头的具体含意吗?下面一条条的为你详细解读,先看 ...
- VINS-mono详细解读
VINS-mono详细解读 极品巧克力 前言 Vins-mono是香港科技大学开源的一个VIO算法,https://github.com/HKUST-Aerial-Robotics/VINS-Mono ...
- SVO详细解读
SVO详细解读 极品巧克力 前言 接上一篇文章<深度滤波器详细解读>. SVO(Semi-Direct Monocular Visual Odometry)是苏黎世大学Scaramuzza ...
随机推荐
- 网络流量监控分析工具 Ntopng 安装
官方说明:http://packages.ntop.org/ http://packages.ntop.org/centos-stable/ http://packages.ntop.o ...
- 关于WCF引用方式之WCF服务寄宿控制台
1.创建解决方案WCFService 依次添加四个项目,如上图,Client和Hosting为控制台应用程序,Service和Service.Interface均为类库. 2.引用关系 Service ...
- async/await的一些用法
普通函数 string Func() { string x = X(); string y = Y(); string z = Z(); return x + y + z; } X(), Y(), Z ...
- sorl基本原理
索引原理 场景:小时候我们都使用过新华字典,妈妈叫你翻开第38页,找到“坑爹”所在的位置,此时你会怎么查呢?毫无疑问,你的眼睛会从38页的第一个字开始从头至尾地扫描,直到找到“坑爹”二字为止.这种搜索 ...
- HDU 1222 Wolf and Rabbit(欧几里得)
Wolf and Rabbit Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)T ...
- Filter command
1. grep egrep fgrep 2. sort sort -d sort -n sort -r sort -f 3. uniq uniq -d uniq -u uniq -c 4. ...
- [转]第一次使用Android Studio时你应该知道的一切配置(三):gradle项目构建
目录: 1.gradle的概念 2.gradle配置jar包,和libs文件夹导入jar包的区别 3.签名打包: (1)Studio (2)命令行 (3)gradle wrapper的原理 4.Bui ...
- JS-基础2
JS基本语法 1.学习javascript的目的? A.增强网页的动态效果. B.改变网页中的元素(能够直接对网页中的元素进行操作). C.加强同后台的数据交互.页面的数据验证. 2.JS在web ...
- VMware 虚拟机中添加新硬盘的方法(转载)
随着在虚拟机中存储的东西的逐渐的增加,虚拟机的硬盘也逐渐告急,因此急需拓展一块新的虚拟磁盘.以下便是在VMware 中添加新的虚拟磁盘的方法: 一.VMware新增磁盘的设置步骤 (建议:在设置虚 ...
- Spring实战之环境与profile
1.配置profile bean Spring为环境相关的bean所提供的解决方案其实与构建时的方案没有太大的差别.当然,在这个过程中需要根据环境决定该创建哪个bean和不创建哪个bean.不过Spr ...
