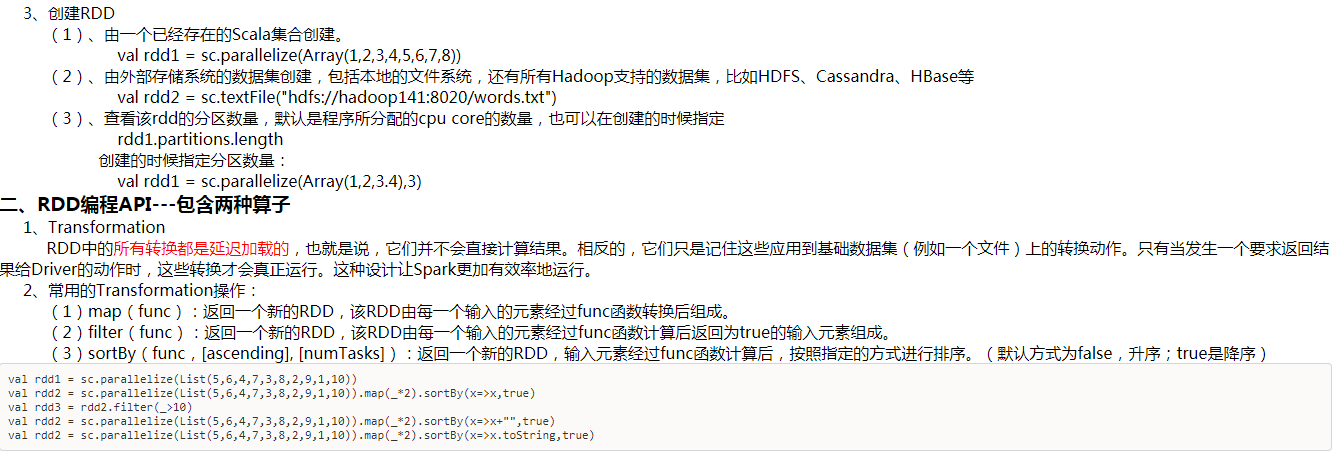
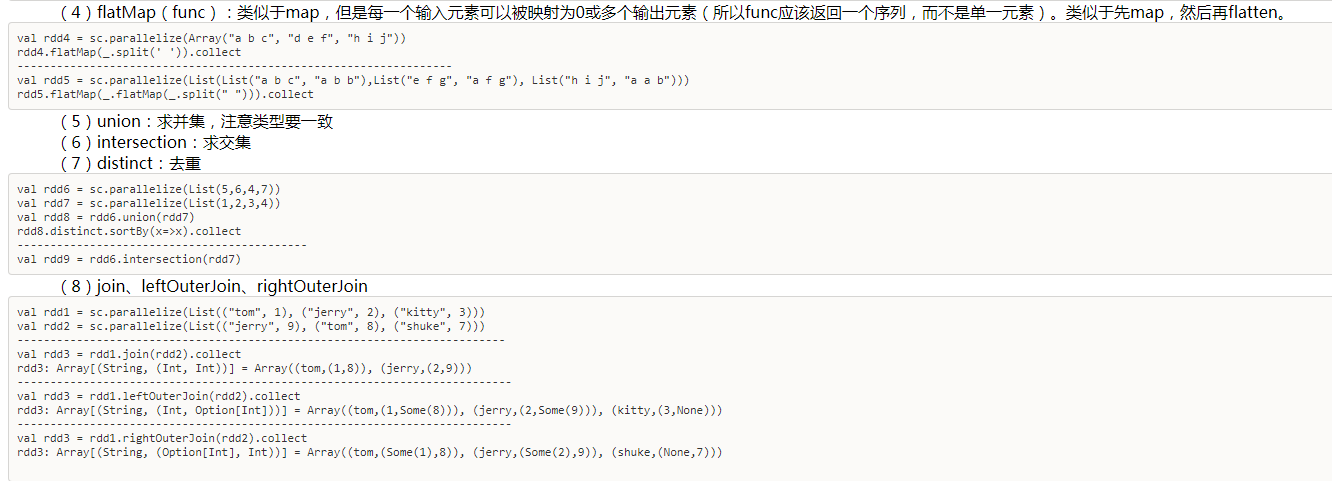
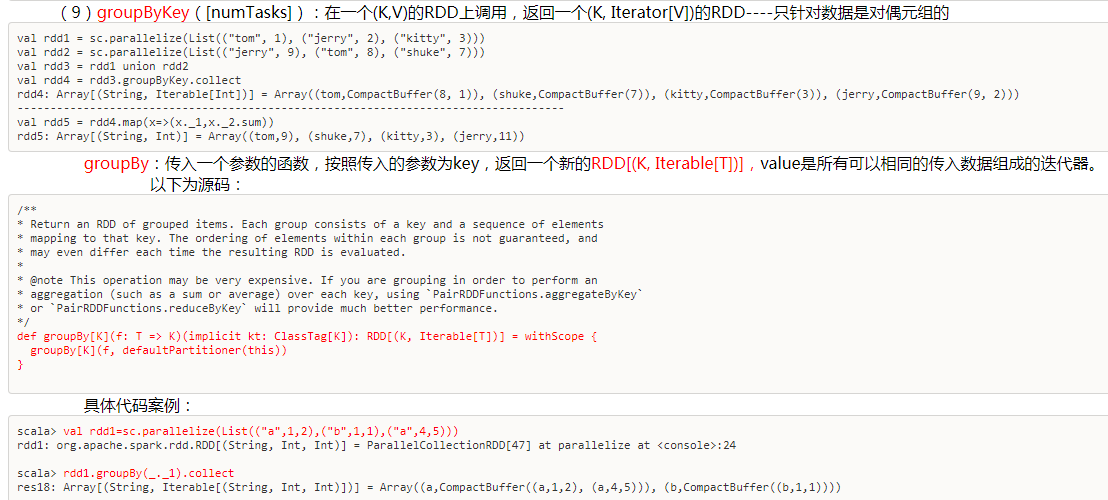
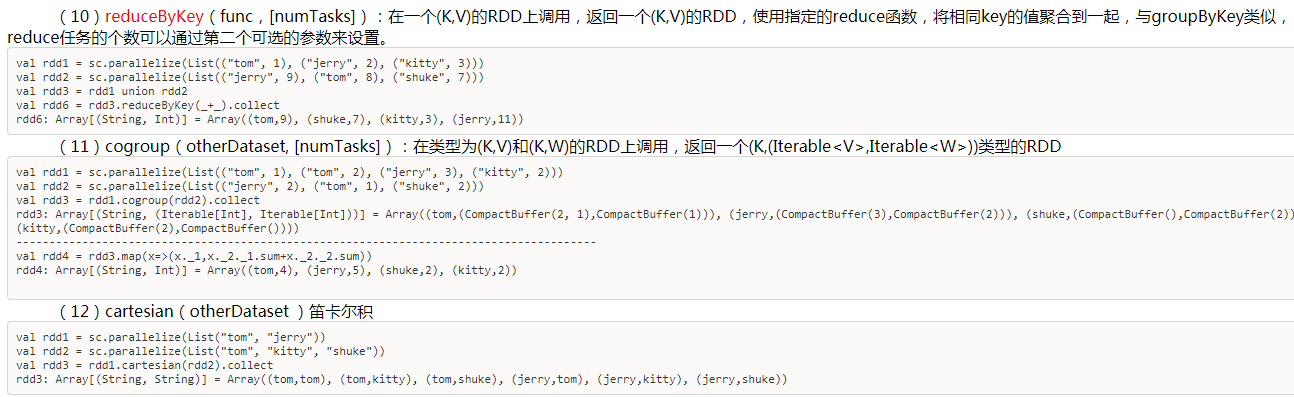
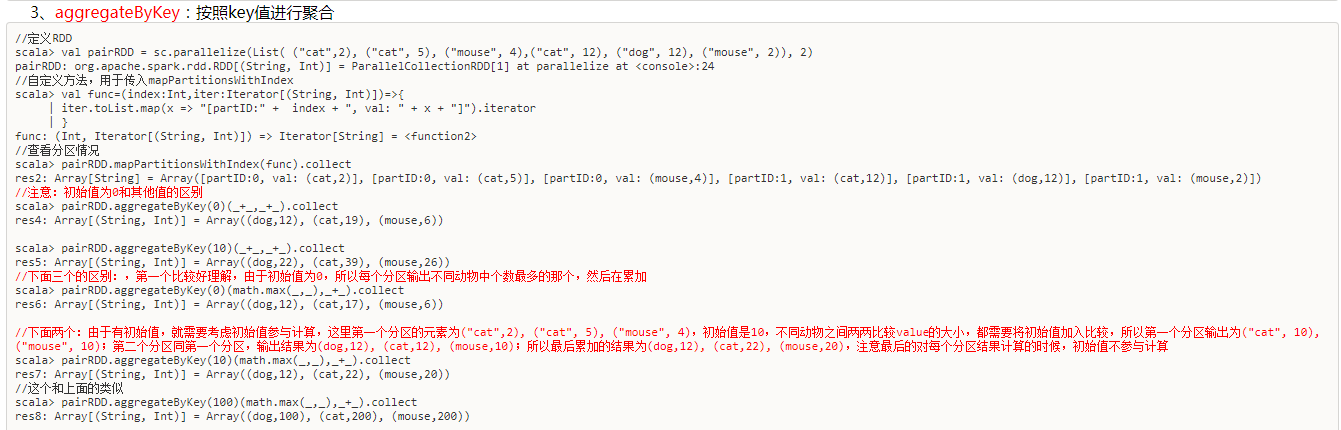
• repartition

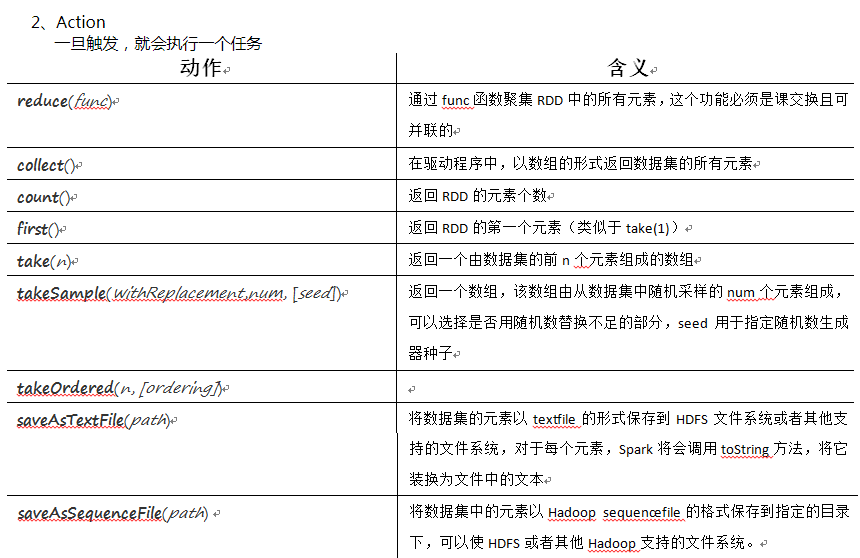
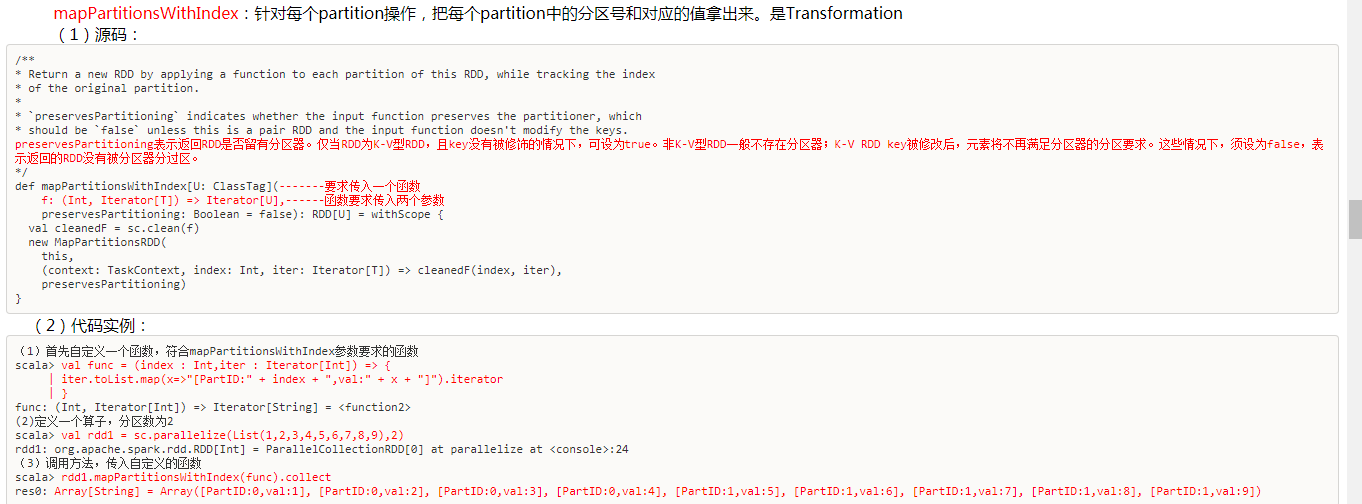
增加或减少分区。会产生shuffle。（多个分区分到一个分区不会产生shuffle）

  • coalesce

coalesce常用来减少分区，第二个参数是减少分区的过程中是否产生shuffle。

true为产生shuffle，false不产生shuffle。默认是false。

如果coalesce设置的分区数比原来的RDD的分区数还多的话，第二个参数设置为false不会起作用，如果设置成true，效果和repartition一样。即repartition(numPartitions) = coalesce(numPartitions,true)

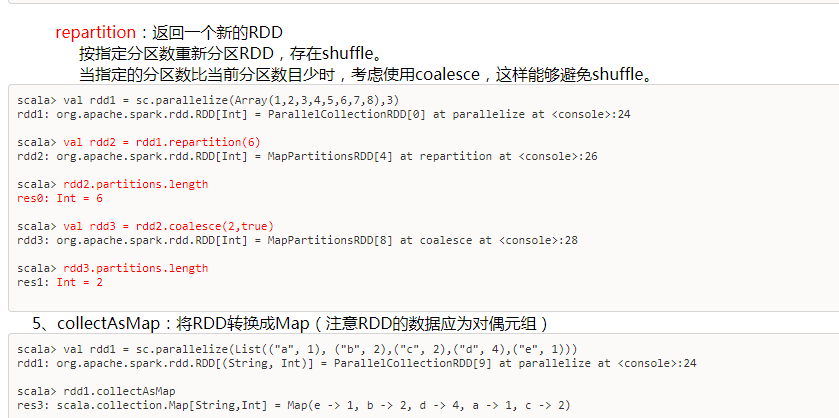
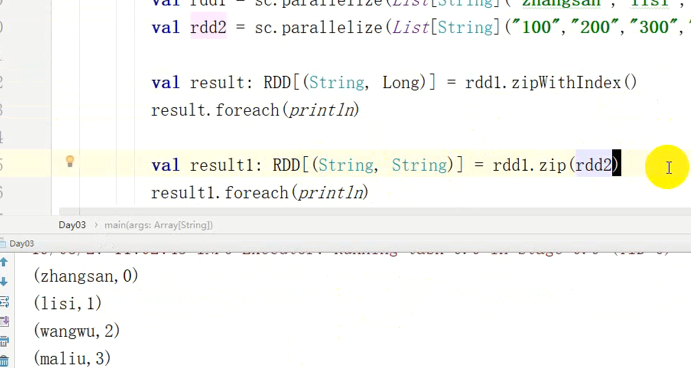
即zipWithIndex（）函数是让RDD从0开始一次记下

而zip（rdd2）则是让两个连接起来（两个必须相等长度）

将两个RDD中的元素（KV格式/非KV格式）变成一个KV格式的RDD,两个RDD的每个分区元素个数必须相同。

RDD介绍与执行的更多相关文章

  1. JAVA RDD 介绍

    RDD 介绍 RDD,全称Resilient Distributed Datasets(弹性分布式数据集),是Spark最为核心的概念,是Spark对数据的抽象. RDD是分布式的元素集合,每个RDD ...

  2. JMeter学习-005-JMeter 主要组件概要介绍及执行顺序

    本文将对 JMeter 主要组件(主要涉及 Threads(Users).Test Fragment.逻辑控制器.配置元件.定时器.前置处理器.Sampler.后置处理器.断言.监听器 十大组件)进行 ...

  3. Spark计算模型-RDD介绍

    在Spark集群背后,有一个非常重要的分布式数据架构,即弹性分布式数据集(Resilient Distributed DataSet,RDD),它是逻辑集中的实体,在集群中的多台集群上进行数据分区.通 ...

  4. SpringMVC简单介绍及执行

    SpringMVC介绍 Spring MVC是Spring提供的一个强大而灵活的web框架.借助于注解,Spring MVC提供了几乎是POJO的开发模式,使得控制器的开发和测试更加简单.这些控制器一 ...

  5. python之commands和subprocess入门介绍(可执行shell命令的模块)

    一.commands模块 1.介绍 当我们使用Python进行编码的时候,但是又想运行一些shell命令,去创建文件夹.移动文件等等操作时,我们可以使用一些Python库去执行shell命令. com ...

  6. Spark—RDD介绍

    Spark-RDD 1.概念介绍 RDD(Resilient Distributed Dataset):弹性分布式数据集,是Spark中最基本的数据抽象,它代表一个不可变.可分区.里面的元素可并行计算 ...

  7. Spring MVC 原理介绍（执行流程）

    Spring MVC工作流程图   图一   图二    Spring工作流程描述       1. 用户向服务器发送请求,请求被Spring 前端控制Servelt DispatcherServle ...

  8. 1.mysql优化---优化入门之MySQL的优化介绍及执行步骤

    优化到底优化什么?      优化,一直是面试最常问的一个问题.因为从优化的角度,优化的思路,完全可以看出一个人的技术积累.那么,关于系统优化,假设这么个场景,用户反映系统太卡(其实就是高并发),那么 ...

  9. SPARKR，对RDD操作的介绍

    (转载)SPARKR,对RDD操作的介绍   原以为,用sparkR不能做map操作, 搜了搜发现可以. lapply等同于map, 但是不能操作spark RDD. spark2.0以后, spar ...

随机推荐

  1. Docker 存储之卷（Volume）

      理解Docker(8):Docker 存储之卷(Volume) (1)Docker 安装及基本用法 (2)Docker 镜像 (3)Docker 容器的隔离性 - 使用 Linux namespa ...

  2. 第六章 声明式服务调用： Spring Cloud Feign

    我们在使用 Spring Cloud Ribbon 时, 通常都会利用它对 RestTemplate 的请求拦截来实现对依赖服务的接口调用, 而 RestTemplate 已经实现了对 HTTP 请求 ...

  3. Python if判断语句

    a=input('输入你的用户名:') if a == "lilei": print('李磊,等你好久了') elif a == "wanghui": prin ...

  4. 左侧倒换菜单 frameset 已过时

    <!doctype html><html><frameset cols="200,*"> <frame src="left.ht ...

  5. 将网页的部分位置嵌入Html网页

    <div align="center" style="margin:0 auto;"> <div style="width:500p ...

  6. WPF DataGrid 控件的运用

    WPF DataGrid 控件的运用 运行环境:Window7 64bit,.NetFramework4.61,C# 6.0: 编者:乌龙哈里 2017-02-23 参考: King Cobra 博客 ...

  7. Python格式符说明

    格式化输出 例如我想输出 我的名字是xxxx 年龄是xxxx name = "Lucy"age = 17print("我的名字是%s,年龄是%d"%(name, ...

  8. Python基础学习八 写日志

    import logging from logging import handlers class Logger(object): level_relations = { 'debug': loggi ...

  9. 【310】◀▶ Python 日期和时间

    参考: python 时间日期计算 Python 日期和时间(菜鸟教程) 8.1. datetime — Basic date and time types python中datetime模块中dat ...

  10. LeetCode之数组处理题java

    342. Power of Four Total Accepted: 7302 Total Submissions: 21876 Difficulty: Easy Given an integer ( ...