决策树C4.5算法——计算步骤示例

使用决策树算法手动计算GOLF数据集

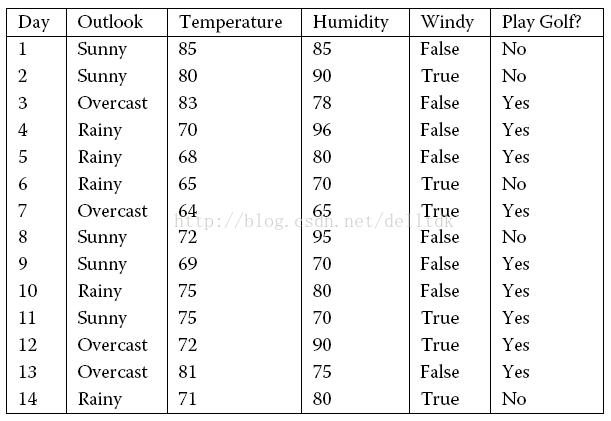
步骤：

1、通过信息增益率筛选分支。

（1）共有4个自变量，分别计算每一个自变量的信息增益率。

首先计算outlook的信息增益。outlook的信息增益Gain(outlook)=

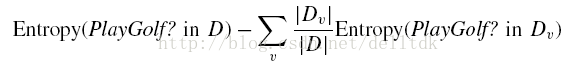
其中，v是可能取值的集合（本例中，outlook可以取3个值），D表示整个数据集，Dv是outlook取值为v的样本集合，而|*|表示数据集的大小（其中的样本数量）。

其中Entropy(PlayGolf? in D)为最终因变量PlayGolf的信息熵值。计算过程为：

PlayGolf共有2种结果：YES（9个观测值）、NO（5个观测值）

YES出现的概率为9/14，NO出现的概率为5/14。

根据熵值计算公式：

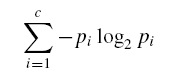
其中c=2（PlayGolf有2个取值YES和NO）。

p1=9/14,p2=5/14.

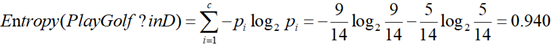
其次计算根据outlook对数据进行分类，加权计算PlayGolf的信息熵

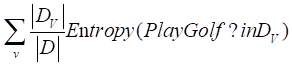
中D表示了1-14全部的PlayGolf数值，但是可以根据outlook的取值不同将1-14行数据，分为3类：Sunny、Overcast、Rainy。

D1表示了为Sunny的PlayGolf的数值。

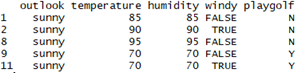
计算D1的中playgolf的信息熵。同理计算D2,D3数据集的PlayGolf信息熵。

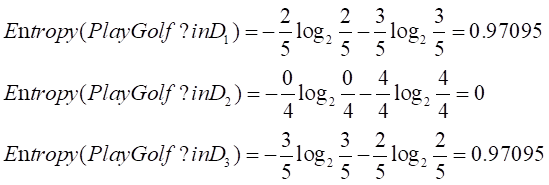
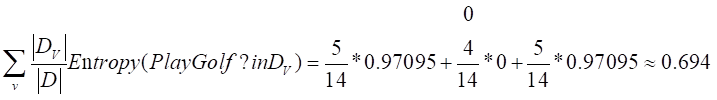
计算属性Outlook的信息增益Gain(Outlook)=0.940-0.694=0.246

信息增益率为：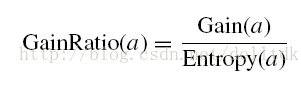

Outlook的信息增益已经有了，现在计算Outlook的熵。

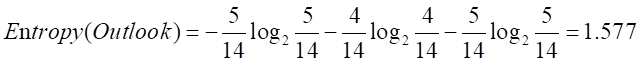
计算Outlook的信息增益率

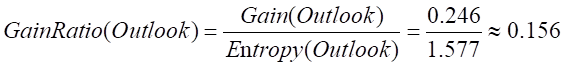
同理计算其他属性的信息增益率。