POJ 1737 Connected Graph 题解（未完成）

Connected Graph

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 3156		Accepted: 1533

Description

An undirected graph is a set V of vertices and a set of E∈{V*V} edges.An undirected graph is connected if and only if for every pair (u,v) of vertices,u is reachable from v.
You are to write a program that tries to calculate the number of different connected undirected graph with n vertices.

For example,there are 4 different connected undirected graphs with 3 vertices.

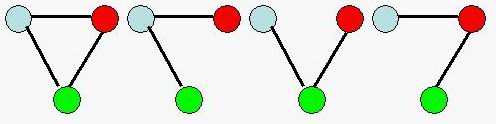
Input

The
input contains several test cases. Each test case contains an integer n,
denoting the number of vertices. You may assume that 1<=n<=50.
The last test case is followed by one zero.

Output

For each test case output the answer on a single line.

Sample Input

1
2
3
4
0

Sample Output

1
1
4
38

Source

LouTiancheng@POJ

————————————————我是华丽丽的分割线——————————————————

据说是男人八题中的第一道

难得我都快不会了...T_T

DP解决。