没办法，SVD就讲的这么好

2）奇异值：

下面谈谈奇异值分解。特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的，在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有N个学生，每个学生有M科成绩，这样形成的一个N * M的矩阵就不可能是方阵，我们怎样才能描述这样普通的矩阵呢的重要特征呢？奇异值分解可以用来干这个事情，奇异值分解是一个能适用于任意的矩阵的一种分解的方法：

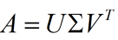    假设A是一个N * M的矩阵，那么得到的U是一个N * N的方阵（里面的向量是正交的，U里面的向量称为左奇异向量），Σ是一个N * M的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值），V’(V的转置)是一个N * N的矩阵，里面的向量也是正交的，V里面的向量称为右奇异向量），从图片来反映几个相乘的矩阵的大小可得下面的图片

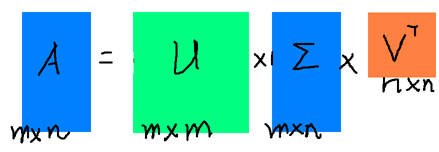
那么奇异值和特征值是怎么对应起来的呢？首先，我们将一个矩阵A的转置 * A，将会得到一个方阵，我们用这个方阵求特征值可以得到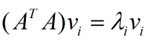：    这里得到的v，就是我们上面的右奇异向量。此外我们还可以得到：

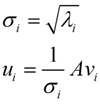    这里的σ就是上面说的奇异值，u就是上面说的左奇异向量。奇异值σ跟特征值类似，在矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解：

r是一个远小于m、n的数，这样矩阵的乘法看起来像是下面的样子：

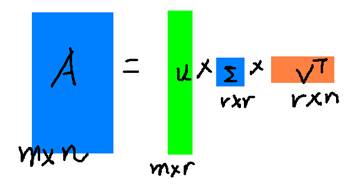
  右边的三个矩阵相乘的结果将会是一个接近于A的矩阵，在这儿，r越接近于n，则相乘的结果越接近于A。而这三个矩阵的面积之和（在存储观点来说，矩阵面积越小，存储量就越小）要远远小于原始的矩阵A，我们如果想要压缩空间来表示原矩阵A，我们存下这里的三个矩阵：U、Σ、V就好了。

假设 m=10000，n=1000，r=100

原始存储：m*n=1000万

优化后存储：m*r=100万；r*r=1万；r*n=10万，合计：111万，是原来存储空间的1/10.

而且在计算的时候，用分解后的矩阵计算，明显减小了矩阵的规模，不至于内存溢出