形式化验证工具（PAT）羊车门代码学习

首先介绍一下PAT工具，下图是PAT工具的图标

PAT工具全称是Process Analysis Toolkit，可以做一些简单的验证。

今天我们分析一下例子里面的Monty Hall Problem

这个问题不知道大家知不知道，这里简单介绍一些这个问题（羊车门问题）。话说有一个国外的电视节目，有三个门（A，B，C门），其中两个门后面放的是羊，另一个门后面放的是车，说一天，一个参与者选中了A这个门，主持人从另外两个门里面选中一个门，打开一看是羊。问参与者要不要换选的门，换门得到车的概率是多大。

我们来简单分析一下这个问题，首先参与者第一个门里面是羊的概率为2/3，是车的概率为1/3，因为另一扇门被打开而且里面是羊，那么如果想换门得到车必须是第一个门是羊，就是概率为2/3，也就是说，在这种情况下，换门得到车的概率是2/3，不换门得到车的概率是1/3。

我们加大一点点难度，假设在参与者选中车之后，有1/3的概率主持人会把车放到参与者选中的门里面，有2/3的概率什么都不做。这种情况下我们看换门得到车的概率是多少。

首先第一次参与者选门，选中车的概率为1/3，选中羊的概率是2/3，先来看看选中车的情况，这时无论主持人动不动手脚，车都在参与者选中的门里面，然后参与者换门，得到车的概率为0。然后来看第一次选中羊的情况，有1/3的概率主持人会把车放到参与者选中的门里面，有2/3的概率什么都不做，换门得到车的情况必须是主持人什么都不做，就是2/3*2/3=4/9。

好，现在我们回到PAT中来。我们来看看PAT能帮我们做什么。

先看代码：

//=======================Model Details===========================
//枚举门1，门2，门3，值分别为0,1,2
enum{Door1, Door2, Door3};

//定义变量
var car = -;
var guess = -;
var goat = -;
var final = false;

#define goal guess == car && final;
//放车，门1车等于0，门2车等于1，门3车等于2
PlaceCar = []i:{Door1,Door2,Door3}@ placecar.i{car=i} -> Skip;
//选中一个门
Guest = pcase {
        : guest.Door1{guess=Door1} -> Skip
        : guest.Door2{guess=Door2} -> Skip
        : guest.Door3{guess=Door3} -> Skip
};
//开门行为，开的门不能是有车，而且不能是选中的门
Goat = []i:{Door1,Door2,Door3}@
       ifb (i != car && i != guess) {
               hostopen.i{goat = i} -> Skip
       };
//换门行为，换的门不能是选中的门，也不能是主持人已经打开的门
TakeOffer = []i:{Door1,Door2,Door3}@
       ifb (i != guess && i != goat) {
               changeguess{guess = i; final = true} -> Stop
       };
//不换门行为，
NotTakeOffer = keepguess{final = true} -> Stop;
//换门
Sys_Take_Offer = PlaceCar; Guest; Goat; TakeOffer;

#assert Sys_Take_Offer reaches goal with prob;
//不换门
Sys_Not_Take_Offer = PlaceCar; Guest; Goat; NotTakeOffer;

#assert Sys_Not_Take_Offer reaches goal with prob;
//先猜，后放车
Sys_With_Dishonest_Program = Guest; PlaceCar; Goat; NotTakeOffer; //place after guessing

#assert Sys_With_Dishonest_Program reaches goal with prob;
//主持人偷偷换车位置，1/3的概率换车，2/3的概率不换车
HostSwitch = pcase {
                : switch{car = guess} -> Skip
                : Skip
       };
//放车，猜车，开羊门，换车位置，换门
Sys_With_Cheating_Host_Switch = PlaceCar; Guest; Goat; HostSwitch; TakeOffer;

#assert Sys_With_Cheating_Host_Switch reaches goal with prob;

Sys_With_Cheating_Host_Not_Switch = PlaceCar; Guest; Goat; HostSwitch; NotTakeOffer;

#assert Sys_With_Cheating_Host_Not_Switch reaches goal with prob;

代码可能需要解释一下，首先是枚举三个门，Door1, Door2, Door3，这三个门的值就是0,1,2。然后定义了三个变量，car表示车在哪个门，car=0就表示car在第一个门，guess表示参与者选中某个门，guess=Door1（也就是guess=0）就表示选中第一个门，goat就表示主持人中间开的门，goat=1就表示主持人打开的是2号门。final表示程序是否进行到最后。final=true就表示程序进行到最后。

接下来定义了一个goal，这个goal是一个bool判断，guess==car&&final。就是表示程序进行到最后且得到车。

接下来定义了几个行为，分别是放车，参与者选门，主持人开门，换门，不换门。

放车：

PlaceCar = []i:{Door1,Door2,Door3}@ placecar.i{car=i} -> Skip;

英文中括号表示选择，就是那个i在Door1，Door2，Door3里面选择，选择之后开始放车（就是给车赋值），然后结束。

参与者选门：

Guest = pcase {
        : guest.Door1{guess=Door1} -> Skip
        : guest.Door2{guess=Door2} -> Skip
        : guest.Door3{guess=Door3} -> Skip
};

pcase表示概率选择，看到有三种情况，概率都是1/3（这里需要注意一下，这里都是1，所以都为1/3，但是有些同学可能就会问了，都写成0.5行不行，这里是不行的，在PAT里面小数点是有含义的，所以不能使用小数，这里都写成2是可以的，但是写成2是不是有点太2了，所以约定俗称的都写成1，但是如果每种情况的概率不一样，就可以写各种不同的数字）。

主持人开门行为：

Goat = []i:{Door1,Door2,Door3}@
       ifb (i != car && i != guess) {
               hostopen.i{goat = i} -> Skip
       };

主持人开门肯定是在三个门里面选择一个门，而且这个门不能是有车的门，也不能是参与者选中的门。然后结束。

参与者换门行为：

TakeOffer = []i:{Door1,Door2,Door3}@
       ifb (i != guess && i != goat) {
               changeguess{guess = i; final = true} -> Stop
       };

参与者换门也是在三个门里面选一个，而且这个门不能是他当前选中的门，也不能是主持人已经打开的门，然后换门，然后游戏结束（guess = i; final = true）。

参与者不换门行为：

NotTakeOffer = keepguess{final = true} -> Stop;

这里就是直接结束（final = true）。

接下来给了几个行为和对行为的分析：

放车，猜门，开羊门，换门，前面分析过，这个过程得到车的概率是2/3.

Sys_Take_Offer = PlaceCar; Guest; Goat; TakeOffer;

下面这个是对这个行为的验证：

#assert Sys_Not_Take_Offer reaches goal with prob;

我们来看分析结果

点击Verification

然后弹出来一个窗口：

点击第一个，然后进行验证

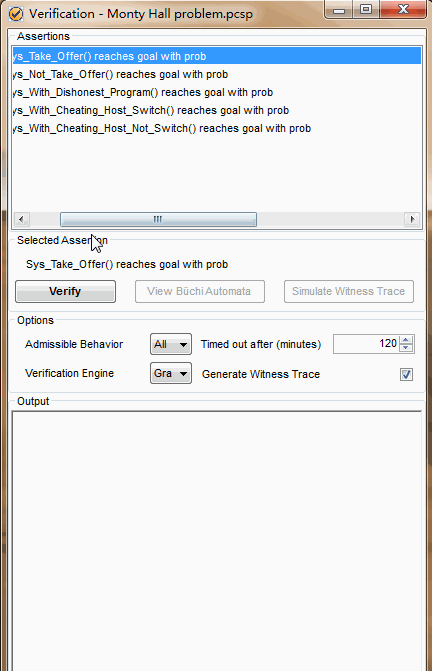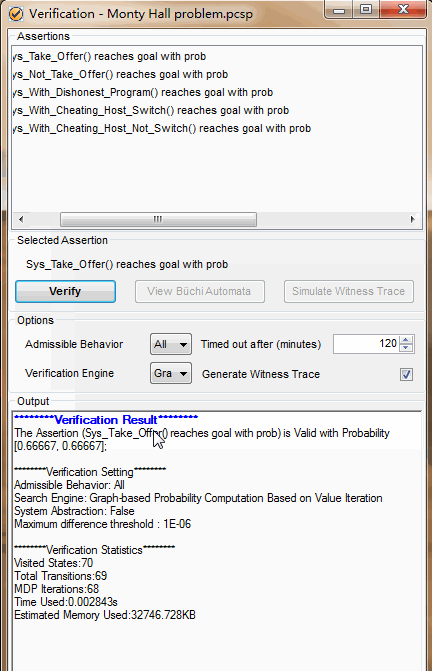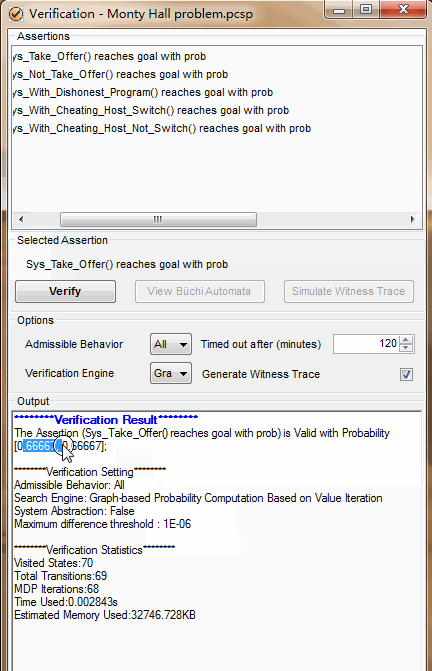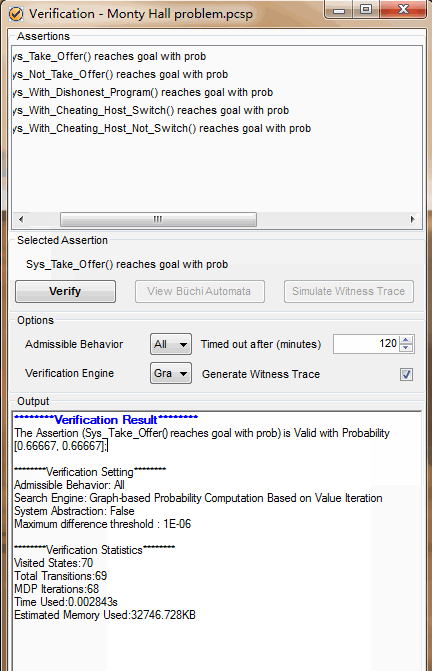
我们接着看后面的代码：

不换门：

Sys_Not_Take_Offer = PlaceCar; Guest; Goat; NotTakeOffer;

分析结果为：

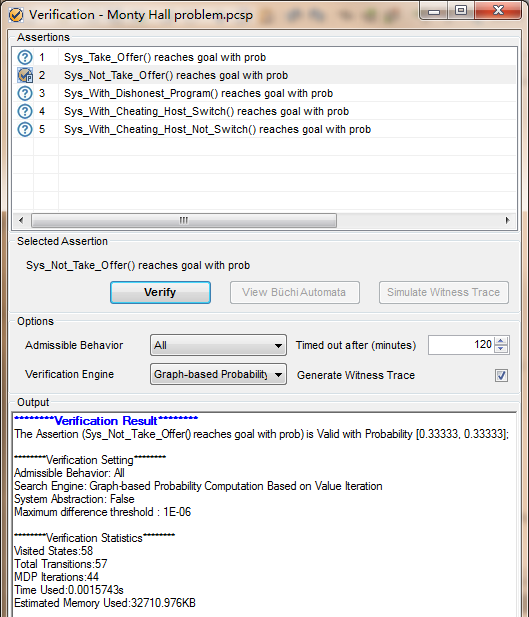
下面来看一个坑爹的行为：

Sys_With_Dishonest_Program = Guest; PlaceCar; Goat; NotTakeOffer; //place after guessing

用户先猜，猜完了猜放车，然后主持人开门，然后不换门，大家觉得这个能中车的概率是多少，必须是从0到1啊。

接下来就是加大难度了，就是主持人有可能换车的位置。

HostSwitch = pcase {
                : switch{car = guess} -> Skip
                : Skip
       };

看到有1/3可能把车放到参与者选中门上。

从上面的分析可以知道这样换门得到车的概率是4/9。不换门得到车的概率是5/9。

如下验证可以看到我们的结果是对的。

可以看到，PAT工具可以做一些简单的概率方面的验证工作。

下次有机会在分享。