（原创）最短路径-Dijkstra算法，以Til the Cows Come Home为例

（1）首先先解释一下单源最短路径：

1）容易的解释：指定一个点（源点）到其余各个顶点的最短路径，也叫做“单源最短路径”

2）官方解释：给定一个带权有向图G=（V,E），其中每条边的权是一个实数。另外，还给定V中的一个顶点，称为源。现在要计算从源到其他所有各顶点的最短路径长度。这里的长度就是指路上各边权之和。这个问题通常称为单源最短路径问题。

（2）解释一下Dijkstra算法：

例如求A点到B、C、D、E、F顶点的最短路径；

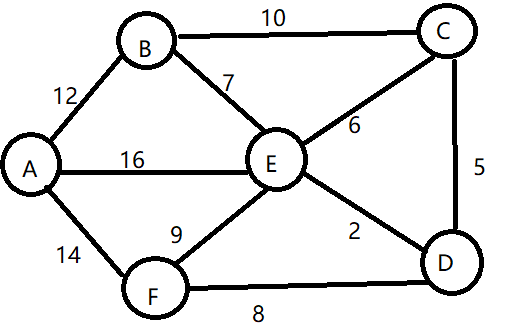
我们可以先这样设想：

1）先把所有的点到另一个点的长度全部初始化为无穷大 ，本身到本身则初始化为0，再输入数值；

第一：将所有点到点初始化为无穷大

代码大致如下：

  const int INF = 0x3f3f3f3f;  //为无穷大；
  int G[][];
  int N  ;//N为点的个数；

          for( i =  ;i <= N ;i++)
          {
              for( j =  ;j <= N ;j++)
              {
                  G[i][j] = INF;
             }
         }

也可用下面这种：

 #include<string.h>
 const int INF = 0x3f3f3f3f;
 int N; //点的个数；
 int G[][];
 memset(G,INF,sizeof(G));

第二：将本身到本身初始化为0 ；因为本身到本身的距离就为0；

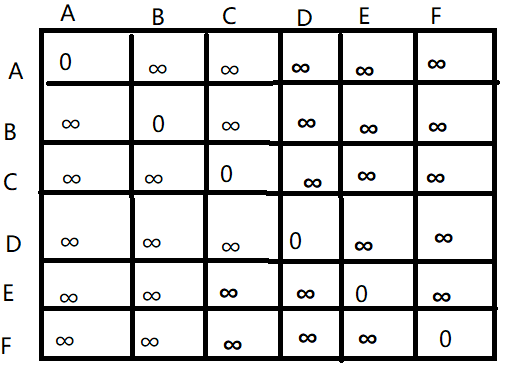
 for(int i =  ;i <= N; i++)
 {
    G[i][i] = ;    //本身到本身距离为0；
 }

第三：输入数据：

对应下面的表格：

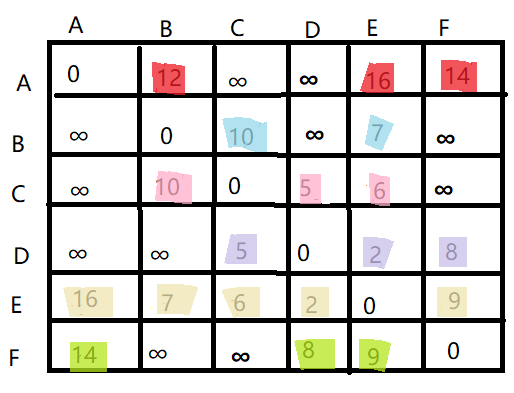
代码实现大概如下：

 int M;        //M为边的个数；
  int x  , y;  // x ,y 为同一边的两个点；
  int D;    //D 为题目给的边的权值；
          for( i = ; i <= M ;i++)
          {
              cin>>x>>y>>D;

                  if(G[x][y]>D)
                  {
                     G[x][y] = D;
                     G[y][x] = D;
                 }

         }

17 //上面我们已经把点到其他点的距离初始化为无穷大，把本身到本身初始化为0；
   //那么上面这个循环的化，我们可以把题目给的两点之间的权值输入；

18 //题目给的权值一定为正值，所以比0大，故本身到本身的距离还是维持为0；
   //而小于无穷大，所以用上面那个循环可把边的权值输入；

2）我们还需用一个一维数组d来存储A顶点到其余各个顶点的初始路程

下面我们来模拟一下：

这是输入最初数据的表格：

模拟：

1)既然是从A点到其余各个顶点的最短路径，那就先找一个离A号顶点最近的顶点。  A到B的距离最小

      

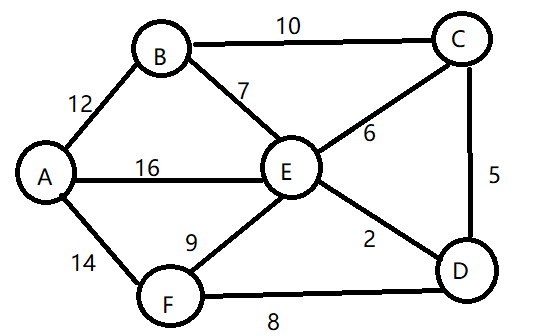
       所以d[2]的值就已经从“估计值”变成了“确定值”，目前离A顶点最近的是B顶点。

2）既然选了B点，接下来看B顶点有哪些出边呢，有B->E和B->C两条边。

先讨论B->E能否让A顶点到E顶点的路程变短；

A->B->E :d[2]+e[2][5]表示从A到B到E的距离；d[2]是A到B顶点的路程，e[2][5]表示B到E的距离；  12+7 = 19;

A->E   :d[5] = 16;

我们发现 d[2]+e[2][5]=19，d[5] = 16;    所以  d[5]  < d[2]+e[2][5];

所以A到E目前的最短距离为16；

     d

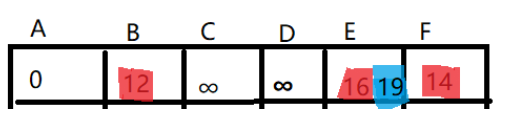
因此d[5]更新为 16；（这个过程有个专业术语叫做：松弛）；

d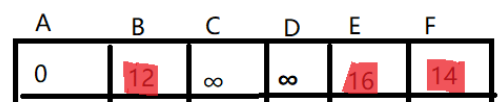

再判断B->C

A->B->C:d[2]+e[2][3] 表示A到B到C的距离；d[2]是A到B顶点的路程，e[2][3]表示B到C 的距离；12+10 = 22；

A->C:A没有直接到C ，所以为无穷大；

22<无穷大

所以A到C目前的最短距离为22；d[3] = 22;

这样从A到B的当前最短路径就更新完了；

3）找除B外离A最近的点：由图可知是F点；

由图可知F的出边有两条：F->E, F->D；

先讨论 F->E能否让A到E的距离变短；

A->F->E ：d[6]+e[6][5] = 14+ 9 = 23;

A->E :d[5] = 16;

所以d[5] < d[6]+e[6][5];

所以当前A到E的最短距离为16；  d[5] = 16;

再讨论E->D的距离能否让A到D的距离变短

A->E->D  :   d[5]+e[5][4] = 16+2=18;

A->D   :   无穷大；

所以A到D的当前最短距离更新为18； d[4] = 18;

4）找除B和F外离A最近的点：即E点

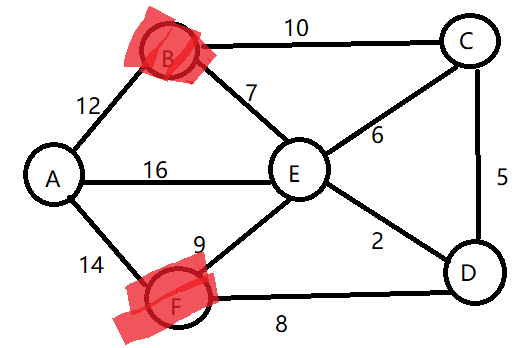
E的出边有C和D，看E->C和E->D能否使A到C的距离变短，使A到D的距离变短；

先讨论E->D

A->E->D ：d[5]+e[5][4] = 16+2 =
18

之前更新后的AD d[4] = 22;

所以AD 当前最短变为18； d[4] = 18;

 讨论E->C，看是否让AC变短

A->E->C ：d[5]+e[5][3] = 16+6
=22;

原更新的AC为22；

所以当前AC最短为22；  d[3] = 22;

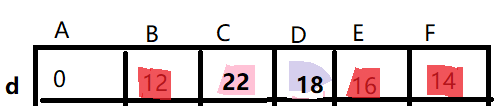
5）找除B,E,F外离A最近的点，即D

 D的出边只有D->C；

看D->C,能否让AC变短；

A->D->C  d[4]+e[4][3] = 18+5 = 23;

原AC   22；

 所以AC当前最短为22；  d[3] = 22;

 

6）最后剩下C

全部找完，确定了A到各个点的最短路径；

下面以一道题为例

Bessie is out in the field and wants to get back to the barn to get as much sleep as possible before Farmer John wakes her for the morning milking. Bessie needs her beauty sleep, so she wants to get back as quickly as possible.

Farmer John's field has N (2 <= N <= 1000) landmarks in it, uniquely
numbered 1..N. Landmark 1 is the barn; the apple tree grove in which Bessie
stands all day is landmark N. Cows travel in the field using T (1 <= T <=
2000) bidirectional cow-trails of various lengths between the landmarks. Bessie
is not confident of her navigation ability, so she always stays on a trail from
its start to its end once she starts it.

Given the trails between the landmarks, determine the minimum distance Bessie
must walk to get back to the barn. It is guaranteed that some such route
exists.

Input

* Line 1: Two integers: T and N

* Lines 2..T+1: Each line describes a trail as three space-separated integers.
The first two integers are the landmarks between which the trail travels. The
third integer is the length of the trail, range 1..100.

Output

* Line 1: A single integer, the minimum distance that Bessie must travel
to get from landmark N to landmark 1.

这道题的题意就是：给定N个地点（编号从1到N），T条道路，先输入两个正整数T和N，接下来T行，每行三个整数，分别代表这条道路的起点和终点和长度，要求求出从N到1的最短路径；此题用Dijkstra算法（先懂得Dijkstra算法才能知道这道题怎么做）

代码如下：  

解法一：未优化的Dijkstra ，时间复杂度为N²；

以上面的思想写就好了，先找出最小，不断更新“当前最小”，并注意标记哪些点已经被访问过了，就是上面被涂红的点；

 #include<iostream>
 #include<string.h>
 #include<stdio.h>
 using namespace std;

 const int INF = 0x3f3f3f3f;
 int N ,M;
 int x , y;
 int min1;
 int D;
 int flag ;
 int vis[];          //用来记录哪些“最近的点”被访问过了；
 int d[];           //用来记录“当前最短距离”；
 int G[][];        //输入点与点间的距离；
 int main()
 {
     while(scanf("%d%d",&M,&N)!=EOF)  //输入边的条数和点的个数；
     {
             for(int i =  ;i <= N ;i++)
         {
             for(int j =  ; j <= N ;j++)
             {
                 G[i][j] = INF;           //先将全部点到点的距离初始化为无穷大；
             }
         }
     for(int i  =  ; i <= N ;i++)
     {
         G[i][i] = ;                  //本身点到本身点距离初始化为0 ；
     }
     for(int i =  ; i <= M ;i++)
     {
         cin>>x>>y>>D;               //输入题目给的点和两点间的距离；
         if(G[x][y]>D)
         {
             G[x][y] = D;          //输入数据；注意这是有向图，所以要正反来一遍；有一些题目从A→B，和从B→A的距离不一样；此题中A→B和B→A一样；
             G[y][x] = D;
         }
     }
     memset(d,INF,sizeof(d));       //就是上面思路中的一位数组d ，用来记录“当前最短距离”；每次更新；
     d[] =  ;          //先初始化d[1] = 0 ；起点1 到1 的距离为0；

     for(int i =  ; i <= N; i++)
     {
         min1 = INF;                      //每次找该点与其他点的最短距离时，先将min1初始化为无穷大；每次循环找新的点到其余点时，就需要min1初始化为INF；
                                        如找i = 1 时与其连通距离最短的点，找到后min1 = d[1]; 后循环后找 i = 2 时与其连通距离最短的点时，应先将min1 再次赋为INF，找到的d[2]才对；
         for(int j =  ; j<= N; j++)
         {
             if(min1>d[j])
             {
    “
                 if(vis[j]==)                   //这是判断没有”被访问过”的点；即还没有被找到的“最近距离”的点；即上面思路中还没被涂红的点；
                 {
                     min1 = d[j];               //找到最小；
                     flag = j;                 //记录该序号；
                 }

             }
         }
         for(int k =  ; k <= N ;k++)
         {
             if(d[k]>d[flag]+G[flag][k])             //不断更新“最近的点”；
             d[k] = d[flag]+G[flag][k];
         }
         vis[flag] = ;                     //标记该点被访问过了；即图中“涂红”点

         }
      cout<<d[N]<<endl;                  //直接输出最短距离；
      for(int i =  ; i <= N; i++)        //多组输入的话，则应将所有“涂红的点”恢复；重新开始新的数据；
      {
          vis[i] = ;
      }
     }

 }

解法二：

下面是优化了的写法，可以用优先队列取优化；每次取最小的时候可以用优先队列去取，时间复杂度优化到了NlogN；

 #include<iostream>
 #include<stdio.h>
 #include<queue>
 #include<string.h>
 using namespace std ;

 const int INF = 0x3f3f3f3f;
 int G[][];
 int d[];

 int i ,j;

 struct node{
     int num;              //记录结点的序号；
     int dis;            //记录结点的“最短距离”
     friend bool operator<(node a ,node b)
     {
         return a.dis>b.dis;//运算符重载，优先队列原本是从大到小输出，现在改写后变成从小到大；
     }
 };

 int main()
 {
     int M , N;
     int x,y,D;

     priority_queue<node>que;//将等下的“最短路径”入队；

     while(scanf("%d%d",&M,&N)!=EOF)
     {
         for( i =  ;i <= N ;i++)
         {
             for( j =  ;j <= N ;j++)
             {
                 G[i][j] = INF;//先全部初始化为无穷大；
             }
         }

             for(int i  =  ; i <= N ;i++)
         {
             G[i][i] = ;
         }
         for( i = ; i <= M ;i++)
         {
             scanf("%d%d%d",&x,&y,&D); //输入数据；

                 if(G[x][y]>D)//如果比无穷大小就更新距离；即有数据的就有数据，无直接连通就是无穷大；
                 {
                     G[x][y] = D;
                     G[y][x] = D;
                 }

         }
         memset(d,0x3f,sizeof(d));
         d[] = ;
         que.push({,}); //将起点入队，起点和起点的距离是为0，因为是本身；
         while(!que.empty())
         {
             node tp = que.top(); //每次取出队列最前的数，即最小的数；

             que.pop();

             for(i =  ;i <= N ;i++)
             {
                 if(G[tp.num][i])//如果两点间有距离
                 {
                     if(d[i]>d[tp.num]+G[tp.num][i])//每次更新“当前最短距离”
                     {
                         d[i] = d[tp.num] + G[tp.num][i];
                         que.push({i,d[i]});//入队；
                     }
                 }
             }
         }

         printf("%d\n",d[N]); //直接输出1到N的最短距离；
         while(!que.empty())  //注意队列要清空；
         {
             que.pop();
         }

     }
     return ;
 }