bzoj 3309 DZY Loves Math 莫比乌斯反演

DZY Loves Math

Time Limit: 20 Sec  Memory Limit: 512 MB
Submit: 1303  Solved: 819
[Submit][Status][Discuss]

Description

对于正整数n，定义f(n)为n所含质因子的最大幂指数。例如f(1960)=f(2^3 * 5^1 * 7^2)=3, f(10007)=1, f(1)=0。
给定正整数a,b，求sigma(sigma(f(gcd(i,j)))) (i=1..a, j=1..b)。

Input

第一行一个数T，表示询问数。
接下来T行，每行两个数a,b，表示一个询问。

Output

对于每一个询问，输出一行一个非负整数作为回答。

Sample Input

4
7558588 9653114
6514903 4451211
7425644 1189442
6335198 4957

Sample Output

35793453939901
14225956593420
4332838845846
15400094813

HINT

【数据规模】

T<=10000

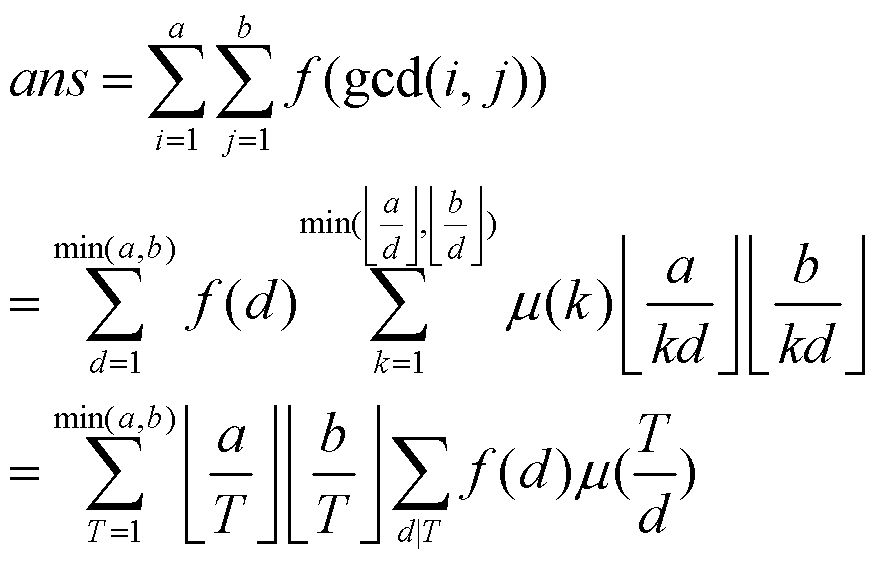
 #pragma GCC optimize(2)
 #pragma G++ optimzie(2)
 #include<cstring>
 #include<cmath>
 #include<cstdio>
 #include<algorithm>
 #include<iostream>

 #define N 10000007
 #define ll long long
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while(!isdigit(ch)){if(ch=='-')f=-;ch=getchar();}
     while(isdigit(ch)){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x*f;
 }

 int n,m;
 int pri[N],tot;
 int t[N],last[N],g[N];
 bool flag[N];

 void init()
 {
     for (int i=;i<N;i++)
     {
         if(!flag[i])
         {
             pri[++tot]=i;
             last[i]=t[i]=g[i]=;
         }
         for(int j=;pri[j]*i<N&&j<=tot;j++)
         {
             int x=i*pri[j];flag[x]=true;
             if(i%pri[j]==)
             {
                 last[x]=last[i];
                 t[x]=t[i]+;
                 if(last[x]==)g[x]=;
                 else g[x]=(t[last[x]]==t[x]?-g[last[x]]:);
                 break;
             }
             else
             {
                 last[x]=i;
                 t[x]=;
                 g[x]=(t[i]==?-g[i]:);
             }
         }
     }
     for (int i=;i<N;i++)g[i]+=g[i-];
 /*    for (int i=11;i<=20;i++)
         cout<<"xzpxzpxzpxzpxzpxzp==laji="<<g[i]<<endl;*/
 }
 ll solve(int n,int m)
 {
     if(n>m)swap(n,m);ll res=;
     for (int i=,last;i<=n;i=last+)
     {
         last=min(n/(n/i),m/(m/i));
         res+=1ll*(n/i)*(m/i)*(g[last]-g[i-]);
     }
     return res;
 }
 int main()
 {
     init();
     int T=read();
     while(T--)
     {
         n=read(),m=read();
         printf("%lld\n",solve(n,m));
     }
 }