PowerDesigner中的域(Domain)的概念及应用

一、概念

域：实际上就是一个取值范围，也可扩展为一个数据类型。域可以定义检查约束、取值范围、最大值、最小值、默认值等。

域是通过用户自定义类型实现的，定义一个域的后，可以实多个实体的属性共享，这也模型设计中非常重要。

例如：“服务生”、“客户”、“操作员”三个实体中都有“姓名”属性，我们就可以定义一个“姓名”域，分别附加到三个实体中，修改域的同时，使用域的实体的相关属性也会随之更新。所图所示

二、域的定义

菜单Model->Domains,在弹出窗口“List of Domains”中,增加新的域。如图所示

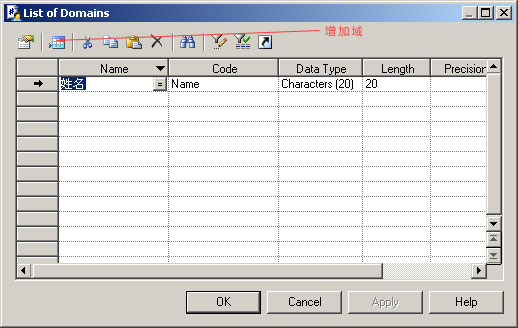
三、附加域到实体属性

在定义某属性的类型和取值范围、约束条件时，对于相同类型的属性，不用逐个去设置相同的取值范围、约束条件等。

只用把该类型的条件定义在域中，添加列时，只用填写列名，并把Domain选择添加的域，则该字段的类型、约束等自动修改为该域的设定值。

打开实体的属性选项卡，如图所示，从Domain下拉列表中选择一个域

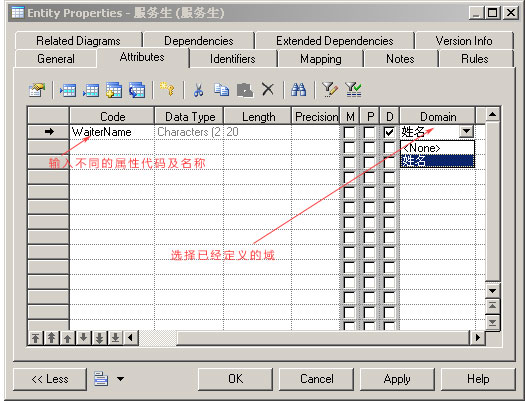
注：设置域与数据项的分离关系，Tools->Model Options ->Model，设置“Domain/Attribute”,Enforce non-divergence 下的Data type(数据类型、长度、精度)、Check（检查约束）、Rules（业务规则）、Mandatory等。如果都不选，则表示设置域与数据项是可分离的。默认为Data type 不可分离，可自行设置。如下图所示

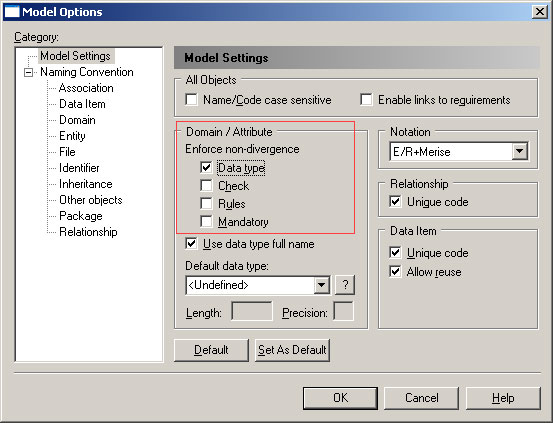
四、附加域到数据项上

菜单Model->Data Items,在弹出窗口“List Data Items”中，添加数据项以及附加域,所图所示