[LeetCode 115] - 不同子序列(Distinct Subsequences)

问题

给出字符串S和T，计算S中为T的不同的子序列的个数。

一个字符串的子序列是一个由该原始字符串通过删除一些字母（也可以不删）但是不改变剩下字母的相对顺序产生的一个新字符串。如，ACE是ABCDE的一个子序列，但是AEC不是。

这里有一个例子：

S＝“rabbbit”，T＝“rabbit”

返回值应为3

初始思路

要找出子序列的个数，首先要有找出S中为T的子序列的方法。T是S的子序列，首先其每一个字母肯定会在S中出现，通过遍历T的每一个字母即可完成这个检查。而根据不能乱序的要求，下一个字母在S中出现的位置不能在上一个字母在S中出现的位置之前。由此，我们得到下面的算法：

循环遍历T

   如果当前字母在S中，而且在S中的位置大于前一个字母在S中的位置

      继续循环

   否则

      返回

循环结束

确认T为S的子序列

上面的算法用来找S中存不存在唯一的T子序列没有问题，但是如果T中的字母在S中出现多次就不靠谱了。当T中字母多次出现在S时，意味着出现了分支。如S：doggy，T：dog。当我们遍历到g字母时，其实出现了取S中两个不同g字母的分支。看到分支，我们可以想到递归：把循环遍历T的过程改为递归，每次递归调用要处理的T的位置加1，递归结束条件为走到T的结尾。经过这样变化，每次递归条件达成意味着一个子序列出现，这样也达到了我们计算子序列个数的目的。

查找子序列（T，要查找的字母在T中的位置，上一个字母在S中的位置）

   如果 要查找的字母在T中的位置 > T的长度

      子序列个数加1

      返回

   如果当前字母在S中

      循环遍历S中所有该字母的位置

         如果当前位置 <=  上一个字母在S中的位置

            继续循环

         查找子序列（T，要查找的字母在T中的位置 ＋ 1， 当前位置）

在上面的伪代码中，我们发现判断当前字母是否在S中并获取它在S中的位置这个功能将会被频繁调用。在具体实现时，我们应该联想到使用关联容器（如map）这种查找速度比较快的数据结构（用以字母为下标的数组也可以，查找速度更快。但是需要考虑大小写字母，非英文字母等情况）。字母可以作为关联容器的key，而一个存放位置信息的序列容器（如vector）可以作为关联容器的值。在进行正式计算前，先遍历S生成这个存放信息的关联容器，这样以后我们就不再需要S本身了。最后得到代码如下：

 class Solution {
     public:
         int numDistinct(std::string S, std::string T)
         {
             if(T.size() >= S.size())
             {
                 if(S == T)
                 {
                     return ;
                 }
                 else
                 {
                     return ;
                 }
             }

             positionInfo_.clear();
             count_ = ;

             for(int i = ; i < S.size(); ++i)
             {
                 if(positionInfo_.find(S[i]) == positionInfo_.end())
                 {
                     positionInfo_[S[i]] = {i};
                 }
                 else
                 {
                     positionInfo_[S[i]].push_back(i);
                 }
             }

             FindDistinct(T, , -);

             return count_;
         }

     private:

         void FindDistinct(std::string& T, int pos, int previousPosInS)
         {
             if(pos > T.size() - )
             {
                 ++count_;
                 return;
             }

             const auto iter = positionInfo_.find(T[pos]);

             for(auto posIter = iter->second.begin(); posIter != iter->second.end(); ++posIter)
             {
                 if(*posIter <= previousPosInS)
                 {
                     continue;
                 }

                 FindDistinct(T, pos + , *posIter);
             }
         }

         std::map<char, std::vector<int>> positionInfo_;

         int count_;
     };

numDistinct

提交后Judge Small顺利通过，但是Judge Large超时了。

优化

针对递归计算的优化方法，通过以前题目的分析我们应该比较有经验了：无非就是通过缓存计算结果避免在递归分支中的重复计算。让我们用例子中的S和T来看看递归过程：

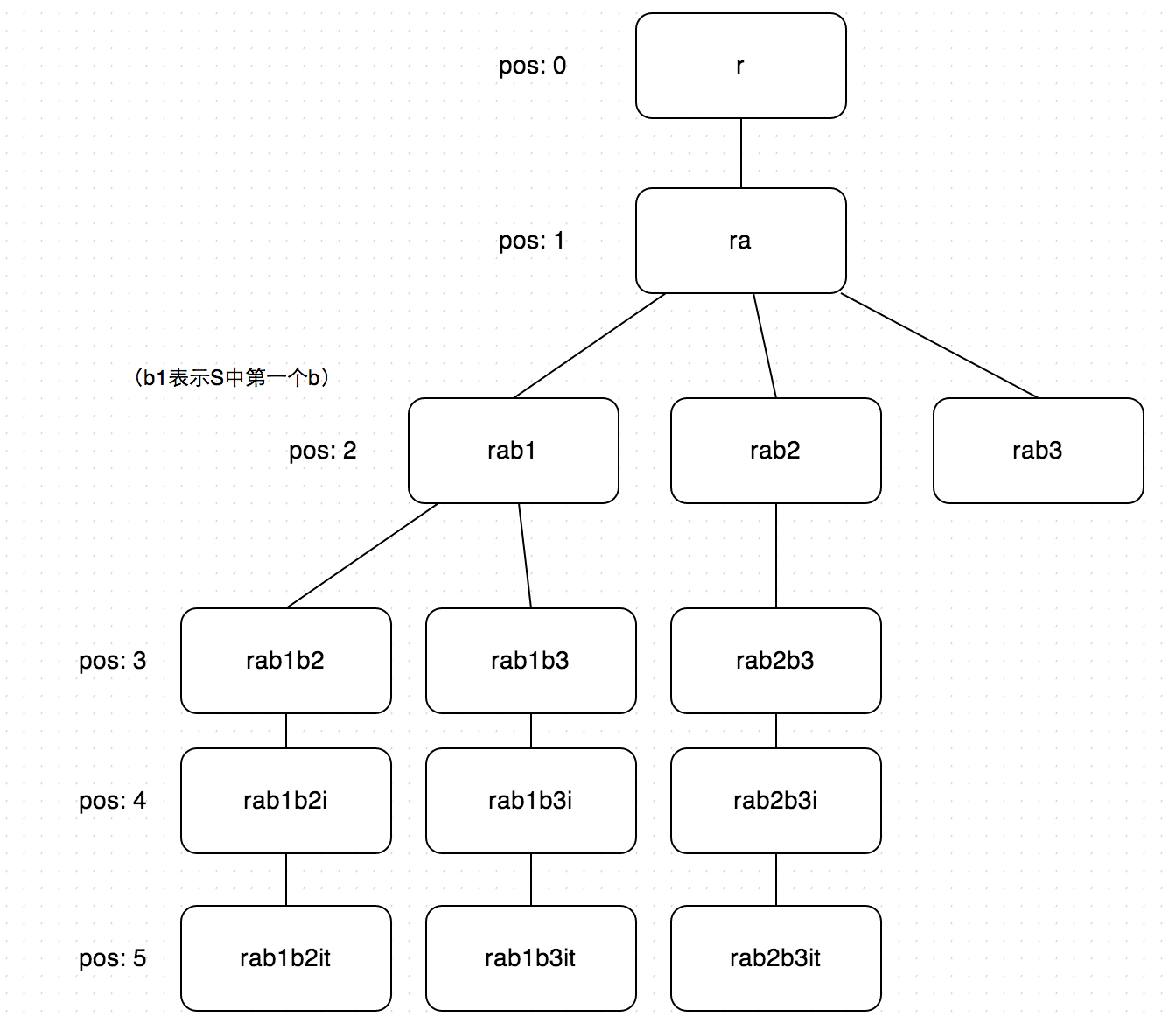
可以看到从T的pos为4的地方存在重复计算，由rab1b2已经可以知道取i后只有1种子序列了。这样看起来似乎可以用T的pos作为key，在rab1b2的递归序列中纪录count[4]=1。随后在rab1b3的递归中到达pos3层后不用继续递归pos4层即可查表得到本次的子序列数1，看起来似乎没有问题。但是当我们回到pos为2的rab1时，就可以发现隐藏的错误了，此时我们记录count[3]=2。紧接着我们开始处理pos2层的rab2的递归，经过查表得到子序列个数为count[3]=2。这显然是错误的，rab2继续递归并没有两种子序列。

分析一下错误的原因，我们发现其实某点开始的子序列的个数不但和当时T的位置有关，还和当时在S中选取的字母在S中的位置有关。因此处理完rab1递归时我们的缓存应该为count[2, 2] = 2（2为第一个b在S中的位置）。这样在处理rab2时，[2，3]是没有缓存的，我们通过递归可以得到正确的值1。而前面提到的count[4]=1的缓存变为count[4, 5]=1（5为i在S中的位置），不会影响结果。

现在可以开始实现代码了，由于需要缓存数据，我们得在原来基础上做一些小修改，不再使用成员变量纪录子序列个数，而是使用返回值。这样子才有办法缓存不同递归序列中的中间结果。至于缓存，使用一个std::map<std::pair<int, int>, int>即可。完成后的代码如下：

 class SolutionV3 {
     public:
         int numDistinct(std::string S, std::string T)
         {
             if(T.size() >= S.size())
             {
                 if(S == T)
                 {
                     return ;
                 }
                 else
                 {
                     return ;
                 }
             }

             positionInfo_.clear();
             cachedResult_.clear();

             for(int i = ; i < S.size(); ++i)
             {
                 if(positionInfo_.find(S[i]) == positionInfo_.end())
                 {
                     positionInfo_[S[i]] = {i};
                 }
                 else
                 {
                     positionInfo_[S[i]].push_back(i);
                 }
             }

             return FindDistinct(T, , -);
         }

     private:

         int FindDistinct(std::string& T, int pos, int posInS)
         {
             if(pos > T.size() - )
             {
                 return ;
             }

             int count = ;
             int result = ;

             const auto iter = positionInfo_.find(T[pos]);

             for(auto posIter = iter->second.begin(); posIter != iter->second.end(); ++posIter)
             {
                 if(*posIter <= posInS)
                 {
                     continue;
                 }

                 CacheKey cacheKey(pos, *posIter);

                 if(cachedResult_.find(cacheKey) != cachedResult_.end())
                 {
                     count += cachedResult_[cacheKey];
                     continue;
                 }

                 result = FindDistinct(T, pos + , *posIter);
                 cachedResult_[cacheKey] = result;
                 count += result;
             }

             return count;
         }

         std::map<char, std::vector<int>> positionInfo_;

         std::map<std::pair<int, int>, int> cachedResult_;

         typedef std::pair<int, int> CacheKey;
     };

numDistinct_cached

顺利通过Judge Large。