acm数论之旅--中国剩余定理

ACM数论之旅9---中国剩余定理(CRT)（壮哉我大中华╰(*°▽°*)╯）

 

中国剩余定理，又名孙子定理o(*≧▽≦)ツ

能求解什么问题呢？

问题：

一堆物品

3个3个分剩2个

5个5个分剩3个

7个7个分剩2个

问这个物品有多少个

解这题，我们需要构造一个答案

我们需要构造这个答案

5*7*inv(5*7,  3) % 3  =  1

3*7*inv(3*7,  5) % 5  =  1

3*5*inv(3*5,  7) % 7  =  1

这3个式子对不对，别告诉我逆元你忘了(*´∇｀*)，忘了的人请翻阅前几章复习

然后两边同乘你需要的数

2 * 5*7*inv(5*7,  3) % 3  =  2

3 * 3*7*inv(3*7,  5) % 5  =  3

2 * 3*5*inv(3*5,  7) % 7  =  2

令

a = 2 * 5*7*inv(5*7,  3)

b = 3 * 3*7*inv(3*7,  5)

c = 2 * 3*5*inv(3*5,  7)

那么

a % 3 = 2

b % 5 = 3

c % 7 = 2

其实答案就是a+b+c

因为

a%5 = a%7 = 0 因为a是5的倍数，也是7的倍数

b%3 = b%7 = 0 因为b是3的倍数，也是7的倍数

c%3 = c%5 = 0 因为c是3的倍数，也是5的倍数

所以

(a + b + c) % 3 = (a % 3) + (b % 3) + (c % 3) = 2 + 0 + 0 = 2

(a + b + c) % 5 = (a % 5) + (b % 5) + (c % 5) = 0 + 3 + 0 = 3

(a + b + c) % 7 = (a % 7) + (b % 7) + (c % 7) = 0 + 0 + 2 = 2

你看你看，答案是不是a+b+c(｡･ω･)ﾉﾞ，完全满足题意

但是答案，不只一个，有无穷个，每105个就是一个答案（105 = 3 * 5 * 7）

根据计算，答案等于233,233%105 = 23

如果题目问你最小的那个答案，那就是23了

以下抄自百度百科

中国剩余定理给出了以下的一元线性同余方程组：

 

中国剩余定理说明：假设整数m1,m2, ... ,mn两两互质，则对任意的整数：a1,a2, ... ,an，

 方程组(S)

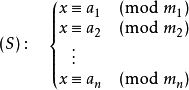
有解，并且通解可以用如下方式构造得到：

设

 

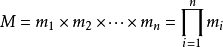
是整数m1,m2, ... ,mn的乘积，并设

 

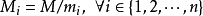
是除了mi以外的n- 1个整数的乘积。

设

 

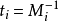
这个就是逆元了

  

通解形式为

  

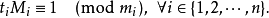
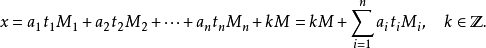
在模M的意义下，方程组(S)只有一个解：

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

我知道你们只要代码(*ﾟ▽ﾟ*)，抛代码，1,2,3，我抛

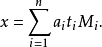
 1 //n个方程：x=a[i](mod m[i]) (0<=i<n)
 2 LL china(int n, LL *a, LL *m){
 3     LL M = 1, ret = 0;
 4     for(int i = 0; i < n; i ++) M *= m[i];
 5     for(int i = 0; i < n; i ++){
 6         LL w = M / m[i];
 7         ret = (ret + w * inv(w, m[i]) * a[i]) % M;
 8     }
 9     return (ret + M) % M;
10 } 

要不要来一道题试试手？

poj 1006

http://poj.org/problem?id=1006

问题描述：

人自出生起就有体力，情感和智力三个生理周期，分别为23，28和33天。一个周期内有一天为峰值，在这一天，人在对应的方面（体力，情感或智力）表现最好。通常这三个周期的峰值不会是同一天。现在给出三个日期，分别对应于体力，情感，智力出现峰值的日期。然后再给出一个起始日期，要求从这一天开始，算出最少再过多少天后三个峰值同时出现。

分析：

因为23 = 23

28 = 2*2*7

33 = 3*11

满足两两互质关系，所以直接套模板就好了

AC代码：

#include<cstdio>
typedef long long LL;
const int N = 100000 + 5;
void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
if (!b) {d = a, x = 1, y = 0;}
else{
ex_gcd(b, a % b, y, x, d);
y -= x * (a / b);
}
}
LL inv(LL t, LL p){//如果不存在，返回-1
LL d, x, y;
ex_gcd(t, p, x, y, d);
return d == 1 ? (x % p + p) % p : -1;
}
LL china(int n, LL *a, LL *m){//中国剩余定理
LL M = 1, ret = 0;
for(int i = 0; i < n; i ++) M *= m[i];
for(int i = 0; i < n; i ++){
LL w = M / m[i];
ret = (ret + w * inv(w, m[i]) * a[i]) % M;
}
return (ret + M) % M;
}
int main(){
LL p[3], r[3], d, ans, MOD = 21252;
int cas = 0;
p[0] = 23; p[1] = 28; p[2] = 33;
while(~scanf("%I64d%I64d%I64d%I64d", &r[0], &r[1], &r[2], &d) && (~r[0] || ~r[1] || ~r[2] || ~d)){
ans = ((china(3, r, p) - d) % MOD + MOD) % MOD;
printf("Case %d: the next triple peak occurs in %I64d days.\n", ++cas, ans ? ans : 21252);
}

}

 1 #include<cstdio>
 2 typedef long long LL;
 3 const int N = 100000 + 5;
 4 void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
 5     if (!b) {d = a, x = 1, y = 0;}
 6     else{
 7         ex_gcd(b, a % b, y, x, d);
 8         y -= x * (a / b);
 9     }
10 }
11 LL inv(LL t, LL p){//如果不存在，返回-1
12     LL d, x, y;
13     ex_gcd(t, p, x, y, d);
14     return d == 1 ? (x % p + p) % p : -1;
15 }
16 LL china(int n, LL *a, LL *m){//中国剩余定理
17     LL M = 1, ret = 0;
18     for(int i = 0; i < n; i ++) M *= m[i];
19     for(int i = 0; i < n; i ++){
20         LL w = M / m[i];
21         ret = (ret + w * inv(w, m[i]) * a[i]) % M;
22     }
23     return (ret + M) % M;
24 }
25 int main(){
26     LL p[3], r[3], d, ans, MOD = 21252;
27     int cas = 0;
28     p[0] = 23; p[1] = 28; p[2] = 33;
29     while(~scanf("%I64d%I64d%I64d%I64d", &r[0], &r[1], &r[2], &d) && (~r[0] || ~r[1] || ~r[2] || ~d)){
30         ans = ((china(3, r, p) - d) % MOD + MOD) % MOD;
31         printf("Case %d: the next triple peak occurs in %I64d days.\n", ++cas, ans ? ans : 21252);
32     }
33
34 }

当然，这个中国剩余定理只是基础，面对更强大的敌人，我们要有更强的武器

比如，m1,m2, ... ,mn两两不保证互质，辣怎么办(っ °Д °)っ

别怕，看我接着抛代码

 1 #include<cstdio>
 2 #include<algorithm>
 3 using namespace std;
 4 typedef long long LL;
 5 typedef pair<LL, LL> PLL;
 6 PLL linear(LL A[], LL B[], LL M[], int n) {//求解A[i]x = B[i] (mod M[i]),总共n个线性方程组
 7     LL x = 0, m = 1;
 8     for(int i = 0; i < n; i ++) {
 9         LL a = A[i] * m, b = B[i] - A[i]*x, d = gcd(M[i], a);
10         if(b % d != 0)  return PLL(0, -1);//答案不存在，返回-1
11         LL t = b/d * inv(a/d, M[i]/d)%(M[i]/d);
12         x = x + m*t;
13         m *= M[i]/d;
14     }
15     x = (x % m + m ) % m;
16     return PLL(x, m);//返回的x就是答案，m是最后的lcm值
17 }

这个代码我不给予解释（因为我不会，哇哈哈哈╰(*°▽°*)╯）

遇到需要的题就去套模板吧

（想知道代码原理的去百度吧，或者看《挑战程序设计竞赛》，我模板是从书里抄来经过杰哥修改的）

比如poj 2891

http://poj.org/problem?id=2891

【题目大意】

给出k个模方程组：x mod ai = ri。求x的最小正值。如果不存在这样的x，那么输出-1.

【题目分析】

由于这道题目里面的ai、ri之间不满足两两互质的性质，所以不能用中国剩余定理直接求解。

辣么。。。。愉快的套这个模板吧

AC代码如下:

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> PLL;
LL a[100000], b[100000], m[100000];
LL gcd(LL a, LL b){
return b ? gcd(b, a%b) : a;
}
void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
if (!b) {d = a, x = 1, y = 0;}
else{
ex_gcd(b, a % b, y, x, d);
y -= x * (a / b);
}
}
LL inv(LL t, LL p){//如果不存在，返回-1
LL d, x, y;
ex_gcd(t, p, x, y, d);
return d == 1 ? (x % p + p) % p : -1;
}
PLL linear(LL A[], LL B[], LL M[], int n) {//求解A[i]x = B[i] (mod M[i]),总共n个线性方程组
LL x = 0, m = 1;
for(int i = 0; i < n; i ++) {
LL a = A[i] * m, b = B[i] - A[i]*x, d = gcd(M[i], a);
if(b % d != 0) return PLL(0, -1);//答案，不存在，返回-1
LL t = b/d * inv(a/d, M[i]/d)%(M[i]/d);
x = x + m*t;
m *= M[i]/d;
}
x = (x % m + m ) % m;
return PLL(x, m);//返回的x就是答案，m是最后的lcm值
}
int main(){
int n;
while(scanf("%d", &n) != EOF){
for(int i = 0; i < n; i ++){
a[i] = 1;
scanf("%d%d", &m[i], &b[i]);
}
PLL ans = linear(a, b, m, n);
if(ans.second == -1) printf("-1\n");
else printf("%I64d\n", ans.first);
}
}

 1 #include<cstdio>
 2 #include<algorithm>
 3 using namespace std;
 4 typedef long long LL;
 5 typedef pair<LL, LL> PLL;
 6 LL a[100000], b[100000], m[100000];
 7 LL gcd(LL a, LL b){
 8     return b ? gcd(b, a%b) : a;
 9 }
10 void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
11     if (!b) {d = a, x = 1, y = 0;}
12     else{
13         ex_gcd(b, a % b, y, x, d);
14         y -= x * (a / b);
15     }
16 }
17 LL inv(LL t, LL p){//如果不存在，返回-1
18     LL d, x, y;
19     ex_gcd(t, p, x, y, d);
20     return d == 1 ? (x % p + p) % p : -1;
21 }
22 PLL linear(LL A[], LL B[], LL M[], int n) {//求解A[i]x = B[i] (mod M[i]),总共n个线性方程组
23     LL x = 0, m = 1;
24     for(int i = 0; i < n; i ++) {
25         LL a = A[i] * m, b = B[i] - A[i]*x, d = gcd(M[i], a);
26         if(b % d != 0)  return PLL(0, -1);//答案，不存在，返回-1
27         LL t = b/d * inv(a/d, M[i]/d)%(M[i]/d);
28         x = x + m*t;
29         m *= M[i]/d;
30     }
31     x = (x % m + m ) % m;
32     return PLL(x, m);//返回的x就是答案，m是最后的lcm值
33 }
34 int main(){
35     int n;
36     while(scanf("%d", &n) != EOF){
37         for(int i = 0; i < n; i ++){
38             a[i] = 1;
39             scanf("%d%d", &m[i], &b[i]);
40         }
41         PLL ans = linear(a, b, m, n);
42         if(ans.second == -1) printf("-1\n");
43         else printf("%I64d\n", ans.first);
44     }
45 }

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long LL;
typedef pair<LL, LL> PLL;
LL a[100000], b[100000], m[100000];
LL gcd(LL a, LL b){
return b ? gcd(b, a%b) : a;
}
void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
if (!b) {d = a, x = 1, y = 0;}
else{
ex_gcd(b, a % b, y, x, d);
y -= x * (a / b);
}
}
LL inv(LL t, LL p){//如果不存在，返回-1
LL d, x, y;
ex_gcd(t, p, x, y, d);
return d == 1 ? (x % p + p) % p : -1;
}
PLL linear(LL A[], LL B[], LL M[], int n) {//求解A[i]x = B[i] (mod M[i]),总共n个线性方程组
LL x = 0, m = 1;
for(int i = 0; i < n; i ++) {
LL a = A[i] * m, b = B[i] - A[i]*x, d = gcd(M[i], a);
if(b % d != 0) return PLL(0, -1);//答案，不存在，返回-1
LL t = b/d * inv(a/d, M[i]/d)%(M[i]/d);
x = x + m*t;
m *= M[i]/d;
}
x = (x % m + m ) % m;
return PLL(x, m);//返回的x就是答案，m是最后的lcm值
}
int main(){
int n;
while(scanf("%d", &n) != EOF){
for(int i = 0; i < n; i ++){
a[i] = 1;
scanf("%d%d", &m[i], &b[i]);
}
PLL ans = linear(a, b, m, n);
if(ans.second == -1) printf("-1\n");
else printf("%I64d\n", ans.first);
}
}