神秘常量0x077CB531，德布莱英序列的恩赐

本文发布于游戏程序员刘宇的个人博客, 转载请注明来源https://www.cnblogs.com/xiaohutu/p/10950011.html

某天我在优化游戏的算法，在将一个个关键数据结构优化全部成位操作后，最终来到最后一座大山前，如何快速计算出这个数值的二进制表示中最后一位的1在哪一位？

首先，我们已知：

将二进制只保留最后一位1的算法：

v & -v 的原理

已知IEEE对有符号整数中负数的定义是所有数值位取反+，首位填1，首位这样正负数加起来既可以为0。

例如：一个8位的整数

A =  ， 取反  ， 取反加1  ，首位填1得到  -A =

A + -A 正好加到最高一位进位后为  

因为取反的时候加1，所以A最后一个为1的位取反后为0，下面我们称为第N位

取反后的第N位为0，后面全为1，再加1后的数值上第N位变成1，后面全为0

此时A和-A里，第N位之后的位全为0，第N位之前的位全为反

所以两个数进行与操作，只有第N位为1

即：   &   =

那么，如何将v&-v转换成N呢？

德布莱英序列

我看到了一段代码：

unsigned int v;

int r;

static const int MultiplyDeBruijnBitPosition[] =

{

  , , , , , , , , , , , , , , , ,

  , , , , , , , , , , , , , , ,

};

r = MultiplyDeBruijnBitPosition[((uint32_t)((v & -v) * 0x077CB531U)) >> ];

计算过程可以理解为：

将0x077CB531U的二进制：

00000111011111001011010100110001

乘以 v&-v，即左移N位，再右移27位，得到的常数在MultiplyDeBruijnBitPosition里查表，得到的结果即是N。

例如乘以  ，（6个0，左移6位）

->

再右移27位

->

得到的数字是27，在数组里是6

很神奇，不是吗？

仔细分析一下这个数字，可以发现，这个数字从每一位分别开始看，连续5位（到结尾循环），是所有5位的二进制数字的全集，而且左移28-31位时，结尾填0，正好序列开始的几个数字也是0。

那么不难理解，从这个数列的第X位任意取5位，都可以得到一个0-31的数字，并且根据查表取出这个数字对应是左移过几位。

为什么会存在这样的序列

把二进制依次写出，如果是两位，我们让每个两位数字的最后一位等于下一个两位数字的第一位， 00-01-11-10，写出 0011，长度为4。

三位，我们让每个三个数字的后两位等于下一个数字前两位，001-011-111-110-101-010-000，写出00111010，长度为8。

四位，见图：

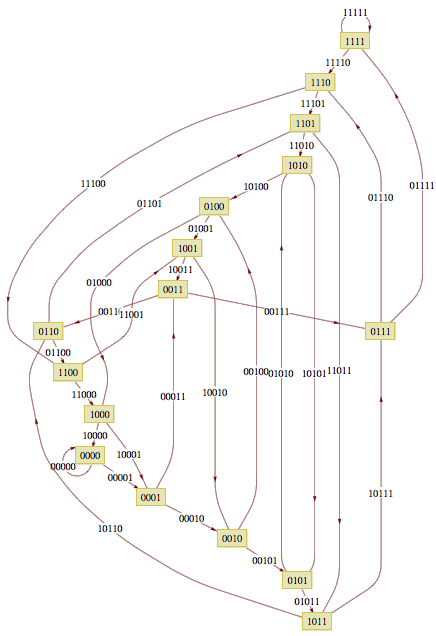
依此类推，到第N位，我们可以让每个数的后N-1位等于下一个数字的前N-1位，得到长度为 2的N次方长度的2进制序列。

这就是德布莱英原理：一定存在长度为2的N次方长度的二进制串，循环来看，一位位移动，可以完整描述所有N位长度的二进制数字的集合。

链接1：https://en.wikipedia.org/wiki/De_Bruijn_sequence

链接2：https://baike.baidu.com/item/德布莱英序列/18898516?fr=aladdin

我们可以任意生成这样的序列吗

稍微经过研究可以发现，Debrujin序列是密码学中运用很广泛的序列，已知原理，可以编程来实现自动求序列的代码。

1. 暴力遍历

2. 递归法 https://blog.csdn.net/lusongno1/article/details/51104737

3. 本原多项式方法 https://blog.csdn.net/sea_sky_cloud/article/details/80932402