HDU6181-求解次短路-A*或者dijkstra

（有任何问题欢迎留言或私聊 && 欢迎交流讨论哦

题意：传送门

 原题目描述在最下面。

 次短路裸题。

思路：

 在dijstra的过程过维护两个数组变量：\(dis1[],dis2[]\)。分别表示到达\(i\)节点的最短距离和次短距离。

 如果当前距离大于次短距离，则更新次短距离。如果更新后次短距离小于最短距离，就交换二者的值。到最后两个数组值就更新就完成了。

AC代码：

dijkstra

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<queue>
#include<set>
#include<string>
#include<cmath>
#define test printf("***\n")
#define ka getchar();getchar()
#define ka1 getchar()
#define iis std::ios::sync_with_stdio(false)
using namespace std;
typedef long long LL;
const int N = 100005;
const int INF = 0x3f3f3f3f;
const LL mod = 10000;
const double eps = 1e-8;
struct lp{
    int to;
    LL w;
    lp(int a,LL b){to=a;w=b;}
    bool operator <(const lp &a)const {
        if(w!=a.w) return w>a.w;
        return to<a.to;
    }
};
vector<lp>mp[N];
LL dis1[N],dis2[N];
int n,m;
void init(){
    for(int i=0;i<=n;++i)mp[i].clear();
}
void dij(int s){
    memset(dis1,0x3f,sizeof(dis1));
    memset(dis2,0x3f,sizeof(dis2));
    dis1[s]=0;
    priority_queue<lp>Q;
    Q.push(lp(s,0));
    while(!Q.empty() ){
        lp x=Q.top();Q.pop();
        int u=x.to;
        if(dis2[u]<x.w)continue;
        for(int i=0;i<mp[u].size();++i){
            lp y=mp[u][i];
            if(dis2[y.to]>(x.w+y.w)){
                dis2[y.to]=x.w+y.w;
                Q.push(lp(y.to,dis2[y.to]));
            }
            if(dis2[y.to]<dis1[y.to]){
                swap(dis2[y.to],dis1[y.to]);
            }
        }

    }
    printf("%lld\n",dis2[n]);
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int a,b,c;
        scanf("%d%d",&n,&m);
        init();
        for(int i=0;i<m;++i){
            scanf("%d%d%d",&a,&b,&c);
            mp[a].push_back(lp(b,c));
            mp[b].push_back(lp(a,c));
        }
        dij(1);
    }
    return 0;
}

A*

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<assert.h>
#include<bitset>
#include<vector>
#include<queue>
#define lson rt<<1
#define rson rt<<1|1
#define lowbit(x) (x)&(-(x))
#define all(x) (x).begin(),(x).end()
#define mk make_pair
#define pb push_back
#define fi first
#define se second
using namespace std;
typedef long long LL;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const int N = (int)1e5 +107;
int n, m, k, st, ed;
int vis[N],time[N];
LL dis[N];
struct lp{
  LL f,g;
  int v;
  friend bool operator <(const lp &a,const lp &b){
    if(a.f==b.f)return a.g>b.g;
    return a.f>b.f;
  }
}aa,bb;
struct lh{
  int v,nex;
  LL w;
}cw[200000+5],rev[200000+5];
int head[N],tot,headd[N],tum;
int q[2500005];
void add(int u,int v,LL w){
  cw[++tot].v=v;cw[tot].nex=head[u];cw[tot].w=w;
  head[u]=tot;

  rev[++tum].v=u;rev[tum].nex=headd[v];rev[tum].w=w;
  headd[v]=tum;
}
void spfa(){
  for(int i = 1; i <= n; i++) dis[i] = INF;
  memset(vis, 0, sizeof(vis));
  int h = 0, t = 1;
  q[0] = ed;
  dis[ed] = 0;
  while(h < t){
    int u = q[h++];
    vis[u] = 0;
    for(int i = headd[u] ; ~i ; i = rev[i].nex){
      int v = rev[i].v;
      LL w = rev[i].w;
      if(dis[v] > dis[u] + w){
        dis[v] = dis[u] + w;
        if(!vis[v]){
          q[t++] = v;
          vis[v] = 1;
        }
      }
    }
  }
}
LL Astar(){
  if(dis[st]==INF)return -1;
  memset(time,0,sizeof(time));
  aa.v=st;aa.f=dis[st];aa.g=0;
  priority_queue<lp>Q;
  Q.push(aa);
  while(!Q.empty()){
    bb = Q.top();Q.pop();
    int u = bb.v;
    time[u]++;
    if(time[u]==k&&u==ed)return bb.g;
    if(time[u]>k)continue;
    for(int i=head[u];~i;i=cw[i].nex){
      int v = cw[i].v;
      aa.v = v;
      aa.g=bb.g+cw[i].w;
      aa.f=aa.g+dis[v];
      Q.push(aa);
    }
  }
  return -1;
}
int main(){
  int tim;
  scanf("%d",&tim);
  while(tim--){
    scanf("%d%d", &n, &m);
    tot=tum=-1;
    memset(head,-1,sizeof(head));
    memset(headd,-1,sizeof(headd));
    for(int i = 0, u, v; i < m; ++i){
      LL w;
      scanf("%d%d%lld", &u, &v, &w);
      add(u,v,w);add(v,u,w);
    }
    st=1;ed=n;
    k=2;
    spfa();
    if(st == ed)k++;
    printf("%lld\n", Astar());
  }
  return 0;
}

####原题目描述：

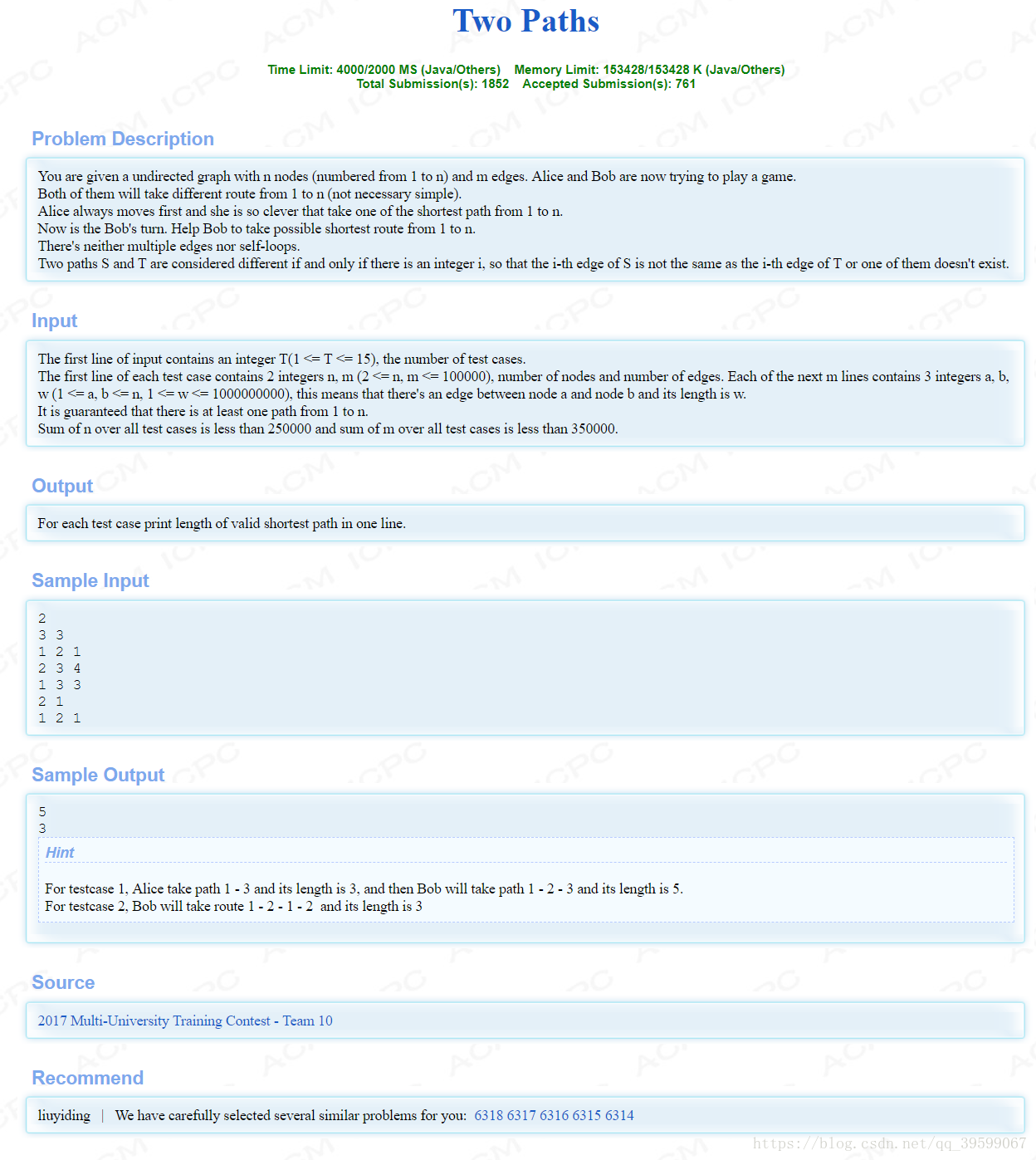
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
#include<queue>
#include<set>
#include<string>
#include<cmath>
#define test printf("***\n")
#define ka getchar();getchar()
#define ka1 getchar()
#define iis std::ios::sync_with_stdio(false)
using namespace std;
typedef long long LL;
const int N = 100005;
const int INF = 0x3f3f3f3f;
const LL mod = 10000;
const double eps = 1e-8;
struct lp{
    int to;
    LL w;
    lp(int a,LL b){to=a;w=b;}
    bool operator <(const lp &a)const {
        if(w!=a.w) return w>a.w;
        return to<a.to;
    }
};
vector<lp>mp[N];
LL dis1[N],dis2[N];
int n, m, pre[N];
void init(){
    for(int i=0;i<=n;++i)mp[i].clear();
}
void dij(int s,LL *dis){
    dis[s]=0;
    priority_queue<lp>Q;
    Q.push(lp(s,0));
    while(!Q.empty() ){
        lp x=Q.top();Q.pop();
        int u=x.to;
        for(int i=0;i<mp[u].size();++i){
            lp y=mp[u][i];
            if(dis[y.to]>(x.w+y.w)){
                dis[y.to]=x.w+y.w;
                pre[y.to]=u;
                Q.push(lp(y.to,dis[y.to]));
            }
        }
    }
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int a,b,c;
        scanf("%d%d",&n,&m);
        init();
        for(int i=0;i<m;++i){
            scanf("%d%d%d",&a,&b,&c);
            mp[a].push_back(lp(b,c));
            mp[b].push_back(lp(a,c));
        }
        memset(dis1,0x3f,sizeof(dis1));
        memset(dis2,0x3f,sizeof(dis2));
        dij(n,dis2);
        memset(pre,0,sizeof(pre));
        dij(1,dis1);
        LL ans = 1e18;
        for(int i=1;i<=n;++i){
            for(int j=0;j<mp[i].size();++j){
                int v= mp[i][j].to;
                LL tmp =dis1[i]+dis2[v]+mp[i][j].w;
                if(pre[v]!=i){
                    if(tmp<ans){
                        ans=tmp;
                    }
                }
            }
        }
        printf("%lld\n", ans);
    }
    return 0;
}