LCT[Link-Cut-Tree学习笔记]

部分摘抄于

FlashHu

candy99

所以文章篇幅较长 请有足够的耐心（不是

其实不用学好splay再学LCT的…/kk （至少现在我平衡树靠fhq）

如果学splay的话…

也许我菜吧…LCT靠背板子 pushup靠理解…没救了/kk

简单讲讲LCT

至于树链剖分 建议在LCT之前学（？

反正我blog里也有

一【理论知识】

-Link-Cut-Tree(简称LCT)是解决动态树类问题一种数据结构

-Preferred Child：重儿子，重儿子与父亲节点在同一棵Splay中，一个节点最多只能有一个重儿子

-Preferred Edge：重边，连接父亲节点和重儿子的边

-Preferred Path ：重链，由重边及重边连接的节点构成的链

-Auxiliary Tree(辅助树)

由一条重链上的所有节点所构成的Splay称作这条链的辅助树

每个点的键值为这个点的深度，即这棵Splay的中序遍历是这条链从链顶到链底的所有节点构成的序列

辅助树的根节点的父亲指向链顶的父亲节点，然而链顶的父亲节点的儿子并不指向辅助树的根节点

（也就是说父亲不认轻儿子只认重儿子，儿子都认父亲）

这条性质为后来的操作提供了依据

原树与辅助树的关系

原树中的重链 -> 辅助树中两个节点位于同一棵Splay中

原树中的轻链 -> 辅助树中子节点所在Splay的根节点的father指向父节点

注意原树与辅助树的结构并不相同

辅助树的根节点≠原树的根节点

辅助树中的father≠原树中的father

辅助树是不断变化的，重链和轻链不断变化

二【实现】

LCT用到的Splay和通常的还是有点不同，没有权值v，不进行查找操作，点编号就是原树的编号

因为是一个Splay森林，多条重链多个根，所以用isRoot(x)判断是否为根，判断isRoot(x)相当于判断x的父亲存不存在

-rotate只是设置g的儿子时判断isRoot(f)就行了

-splay需要pushDown了(因为没有kth了)，也是判断isRoot(pa)

-Access和Cut更新了儿子关系，所以需要update

-Access 将一个点与原先的重儿子切断，并使这个原树上点到根路径上的边全都变为重边

所以 这个节点到根的路径上的所有节点形成了一棵Splay

便于操作或查询节点到根路径上的所有节点

实现：不断把x splay到当前Atree的根，然后它的右子树就是重儿子了，修改；用y辅助 注意：Access后x不一定为这颗Splay的根，因为中途x变fa了 维护了节点信息别忘更新

MakeRoot 将x设为原树的根实现：Access后splay到根，然后全在x的左子树上(权值是深度)，区间翻转即可

FindRoot 找x所在原树根，判连通性 实现：MakeRoot后不断往左找(不需要pushDown？加上也可以啊。不加也对因为只是来判连通，判断是不是在一棵原树上，都不pushDown找到的还是同一个点吧)

Link 实现：MakeRoot(x)然后t[x].fa=y

Cut 实现：MakeRoot(x)然后Access(y) splay(y) ，x就在y的左儿子了，t[y].ch[0]=t[x].fa=0;

维护了节点信息别忘更新

对x到y路径上的点进行修改或查询

只需要对x进行Move_To_Root操作，然后对y进行Access+Splay操作，那么x到y路径上的所有点都在以y为根的子树上

因为Access后x和y重链在一棵Splay上，x深度比y小

====================================================================== 以上是 candy99 巨佬的总结内容（？

像树剖一样……将某一个儿子的连边划分为实边，而连向其他子树的边划分为虚边。

区别在于虚实是可以动态变化的，因此要使用更高级、更灵活的Splay来维护每一条由若干实边连接而成的实链。

基于性质更加优秀的实链剖分，LCT(Link-Cut Tree)应运而生。

LCT维护的对象其实是一个森林。

在实链剖分的基础下，LCT资磁更多的操作

• 查询、修改链上的信息（最值，总和等）
• 随意指定原树的根（即换根）
• 动态连边、删边
• 合并两棵树、分离一棵树（跟上面不是一毛一样吗）
• 动态维护连通性（代替并查集）

边分为实边和虚边，实边包含在Splay中，而虚边总是由一棵Splay指向另一个节点（指向该Splay中中序遍历最靠前的点在原树中的父亲）。

因为性质2，当某点在原树中有多个儿子时，只能向其中一个儿子拉一条实链（只认一个儿子），而其它儿子是不能在这个Splay中的。

那么为了保持树的形状，我们要让到其它儿子的边变为虚边，由对应儿子所属的Splay的根节点的父亲指向该点，而从该点并不能直接访问该儿子（认父不认子）。

接着往下看…

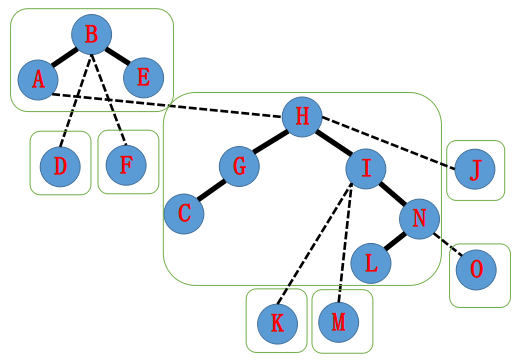
有一棵树，假设一开始实边和虚边是这样划分的（虚线为虚边）

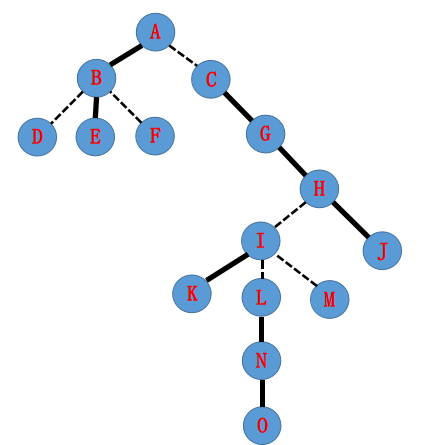
那么所构成的LCT可能会长这样（绿框中为一个Splay，可能不会长这样，但只要满足中序遍历按深度递增（性质1）就对结果无影响）

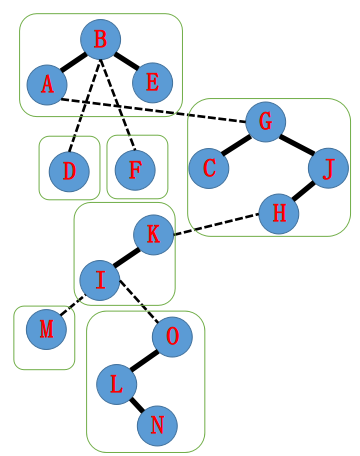
现在我们要access(N)，把A−N的路径拉起来变成一条Splay。

因为性质2，该路径上其它链都要给这条链让路，也就是把每个点到该路径以外的实边变虚。

所以我们希望虚实边重新划分成这样。

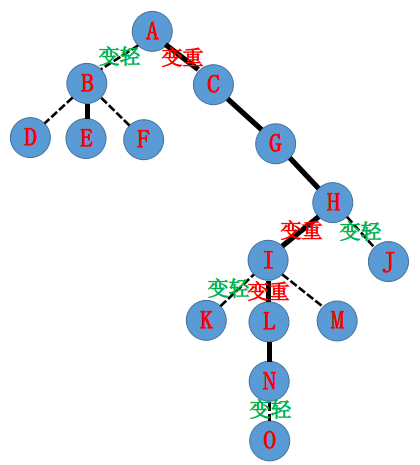
然后怎么实现呢？

我们要一步步往上拉。

首先把splay(N)，使之成为当前Splay中的根。

为了满足性质2，原来N−O的重边要变轻。

因为按深度O在N的下面，在Splay中O在N的右子树中，所以直接单方面将N的右儿子置为0（认父不认子）

然后就变成了这样——

我们接着把N所属Splay的虚边指向的I（在原树上是L的父亲）也转到它所属Splay的根，splay(I)。

原来在I下方的重边I−K要变轻（同样是将右儿子去掉）。

这时候I−L就可以变重了。因为L肯定是在I下方的（刚才L所属Splay指向了I），所以I的右儿子置为N，满足性质1。

然后就变成了这样——

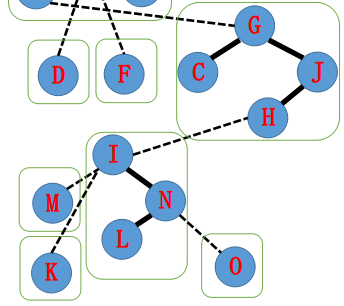
I指向H，接着splay(H)，H的右儿子置为I。



H指向A，接着splay(A)，A的右儿子置为H。

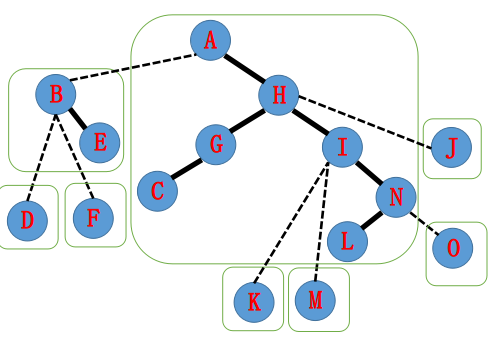
A−N的路径已经在一个Splay中了，大功告成！

代码其实很简单。循环处理，只有四步——

转到根；

换儿子；

更新信息；

当前操作点切换为轻边所指的父亲，转1

  inline void access(int x) { for(int tp = 0 ; x ; x = fa[tp = x]) splay(x) , rs(x) = tp , pushup(x) ; }

只是把根到某个节点的路径拉起来并不能满足我们的需要。更多时候，我们要获取指定两个节点之间的路径信息。

然而一定会出现路径不能满足按深度严格递增的要求的情况。根据性质1，这样的路径不能在一个Splay中。

Then what can we do?

makeroot定义为换根，让指定点成为原树的根。

这时候就利用到access(x)和Splay的翻转操作。

access(x)后x在Splay中一定是深度最大的点对吧。

splay(x)后，x在Splay中将没有右子树（性质1）。于是翻转整个Splay，使得所有点的深度都倒过来了，x没了左子树，反倒成了深度最小的点（根节点），达到了我们的目的。

代码

  inline void makeroot(int x) { access(x) ; splay(x) ; pushr(x) ; }

findroot(x)

找x所在原树的树根，主要用来判断两点之间的连通性（findroot(x)==findroot(y)表明x,y在同一棵树中）

  inline int findroot(int x) { access(x) ; splay(x) ; while(ls(x)) { pushdown(x) ; x = ls(x) ; splay(x) ; } return x ; }

同样利用性质1，不停找左儿子，因为其深度一定比当前点深度小。

split(x,y)

神奇的makeroot已经出现，我们终于可以访问指定的一条在原树中的链啦！

split(x,y)定义为拉出x−y的路径成为一个Splay（本蒟蒻以y作为该Splay的根）

  inline void split(int x , int y) { makeroot(x) ; access(y) ; splay(y) ; }

Link 和 Cut 就是字面意思 连边建边 具体写法

  inline void cut(int x , int y) { makeroot(x) ; if(findroot(y) == x && fa[y] == x && ! ls(y)) fa[y] = ls(x) = 0 , pushup(x) ; }
  inline void link(int x , int y) { makeroot(x) ; if(findroot(y) != x) fa[x] = y ; }

下面给板子和题目（？

#include<bits/stdc++.h>
using namespace std ;
const int N = 1e5 + 10 ;
int n , m , val[N] ;
inline int read() {
	register int x = 0 , f = 1 ;
	register char c = getchar() ;
	for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
	for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
	return x * f ;
}
class LCT {
public:
  int ch[N][2] , fa[N] , sum[N] , rev[N] ;
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
  inline bool isroot(int x) { return ls(fa[x]) != x && rs(fa[x]) != x ; }
  inline bool getr(int x) { return rs(fa[x]) == x ; }
  inline void pushup(int x) { sum[x] = sum[ls(x)] ^ sum[rs(x)] ^ val[x] ; }
  inline void pushr(int x) { rev[x] ^= 1 ; swap(ls(x) , rs(x)) ; }
  inline void pushdown(int x) { if(rev[x]) { if(ls(x)) pushr(ls(x)) ; if(rs(x)) pushr(rs(x)) ; rev[x] ^= 1 ; } }
  inline void rotate(int x) {
    int y = fa[x] , z = fa[y] , k = getr(x) , w = ch[x][k ^ 1] ; if(! isroot(y)) ch[z][getr(y)] = x ;
    fa[fa[fa[ch[ch[x][k ^ 1] = y][k] = w] = y] = x] = z ; pushup(y) ; pushup(x) ;
  }
  inline void pushall(int x) { if(! isroot(x)) pushall(fa[x]) ; pushdown(x) ; }
  inline void splay(int x) {
    pushall(x) ; while(! isroot(x)) { int y = fa[x] ; if(! isroot(y)) rotate(getr(x) ^ getr(y) ? x : y) ; rotate(x) ; }
  }
  inline void access(int x) { for(int tp = 0 ; x ; x = fa[tp = x]) splay(x) , rs(x) = tp , pushup(x) ; }
  inline void makeroot(int x) { access(x) ; splay(x) ; pushr(x) ; }
  inline void split(int x , int y) { makeroot(x) ; access(y) ; splay(y) ; }
  inline int findroot(int x) { access(x) ; splay(x) ; while(ls(x)) { pushdown(x) ; x = ls(x) ; splay(x) ; } return x ; }
  inline void cut(int x , int y) { makeroot(x) ; if(findroot(y) == x && fa[y] == x && ! ls(y)) fa[y] = ls(x) = 0 , pushup(x) ; }
  inline void link(int x , int y) { makeroot(x) ; if(findroot(y) != x) fa[x] = y ; }
  inline void change(int x , int y) { splay(x) ; val[x] = y ; }
  inline int query(int x , int y) { return split(x , y) , sum[y] ; }
} lct ;
signed main() {
  n = read() ; m = read() ;
  for(register int i = 1 ; i <= n ; i ++) cin >> val[i] ;
  for(register int i = 1 ; i <= m ; i ++) {
    int opt = read() ;
    if(opt == 0) { int x = read() , y = read() ; printf("%d\n" , lct.query(x , y)) ; }
    if(opt == 1) { int x = read() , y = read() ; lct.link(x , y) ; }
    if(opt == 2) { int x = read() , y = read() ; lct.cut(x , y) ; }
    if(opt == 3) { int x = read() , y = read() ; lct.change(x , y) ; }
  }
  return 0 ;
}

[国家集训队]Tree II

带修的LCT 就直接像线段树一样放标记然后搞一下更新就可以了

#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using uint = unsigned int ;
using namespace std ;
const int N = 1e5 + 5 ;
const int Mod = 51061 ;
uint n , q , fa[N] , ch[N][2] , val[N] , sum[N] , sz[N] , mul[N] , add[N] ;
bool rev[N] ;
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
inline void Add(uint & x , uint y) { x += y ; x %= Mod ; }
inline void Mul(uint & x , uint y) { x *= y ; x %= Mod ; }
inline bool isroot(uint x) { return (ls(fa[x]) != x) && (rs(fa[x]) != x) ; }
inline void pushup(uint x) { sum[x] = (sum[ls(x)] + sum[rs(x)] + val[x]) ; sum[x] %= Mod ; sz[x] = (sz[ls(x)] + sz[rs(x)] + 1) ; }
inline void pushr(uint x) { swap(ls(x) , rs(x)) ; rev[x] ^= 1 ; }
inline void pushm(uint x , uint v) { Mul(sum[x] , v) ; Mul(val[x] , v) ; Mul(mul[x] , v) ; Mul(add[x] , v) ; }
inline void pusha(uint x , uint v) { Add(sum[x] , v * sz[x]) ; Add(val[x] , v) ; Add(add[x] , v) ; }
inline void pushdown(uint x) {
  if(mul[x] != 1) { pushm(ls(x) , mul[x]) ; pushm(rs(x) , mul[x]) ; mul[x] = 1 ; }
  if(add[x]) { pusha(ls(x) , add[x]) ; pusha(rs(x) , add[x]) ; add[x] = 0 ; }
  if(rev[x]) { if(ls(x)) pushr(ls(x)) ; if(rs(x)) pushr(rs(x)) ; rev[x] = 0 ; }
}
inline bool getr(uint x) { return rs(fa[x]) == x ; }
inline void rotate(uint x) { uint y = fa[x] , z = fa[y] , k = getr(x) , w = ch[x][k ^ 1] ;
  if(! isroot(y)) ch[z][getr(y)] = x ;
  ch[x][k ^ 1] = y ; ch[y][k] = w ;
  if(w) fa[w] = y ; fa[y] = x ; fa[x] = z ;
  pushup(y) ;
}
inline void pushall(uint x) { if(! isroot(x)) pushall(fa[x]) ; pushdown(x) ; }
inline void splay(uint x) { pushall(x) ;
  while(! isroot(x)) { uint y = fa[x] ;
    if(! isroot(y)) { rotate(getr(y) ^ getr(x) ? x : y) ; }
    rotate(x) ;
  } pushup(x) ;
}
inline void access(uint x) { for(uint tp = 0 ; x ; tp = x , x = fa[tp]) splay(x) , rs(x) = tp , pushup(x) ; }
inline void makeroot(uint x) { access(x) ; splay(x) ; pushr(x) ; }
inline void split(uint x , uint y) { makeroot(x) ; access(y) ; splay(y) ; }
inline void link(uint x , uint y) { makeroot(x) ; fa[x] = y ; }
inline void cut(uint x , uint y) { split(x , y) ; fa[x] = ls(y) = 0 ; }
signed main() {
  ios :: sync_with_stdio(false) ;
  cin.tie(nullptr) ;
  cout.tie(nullptr) ;
  cin >> n >> q ;
  for(register int i = 1 ; i <= n ; i ++) val[i] = mul[i] = 1 ;
  for(register int i = 1 ; i <= n - 1 ; i ++) { uint u , v ; cin >> u >> v ; link(u , v) ; }
  for(register int i = 1 ; i <= q ; i ++) {
    char c ; cin >> c ;
    if(c == '+') { uint u , v , w ; cin >> u >> v >> w ; split(u , v) ; pusha(v , w) ; }
    if(c == '-') { uint u , v , u2 , v2 ; cin >> u >> v >> u2 >> v2 ; cut(u , v) ; link(u2 , v2) ; }
    if(c == '*') { uint u , v , w ; cin >> u >> v >> w ; split(u , v) ; pushm(v , w) ; }
    if(c == '/') { uint u , v ; cin >> u >> v ;  split(u , v) ; cout << sum[v] << '\n' ; }
  }
  return 0 ;
}

[COCI 2009] OTOCI / 极地旅行社

板子…不说了

#include<bits/stdc++.h>
using namespace std ;
#define csp rp++

inline int read() { register int x = 0 , f = 1 ; register char c = getchar() ;
  for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
  for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
  return x * f ;
}

int n ;
const int N = 1e5 + 10 ;
int val[N] ;
int ch[N][2] ; int fa[N] ; int sum[N] ; bool rev[N] ;
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
inline bool isroot(int x) { return ls(fa[x]) != x && rs(fa[x]) != x ; }
inline bool getr(int x) { return rs(fa[x]) == x ; }
inline void pushup(int x) { sum[x] = sum[ls(x)] + sum[rs(x)] + val[x] ; }
inline void pushr(int x) {
  if(! rev[x]) return ;
  swap(ls(x) , rs(x)) ;
  rev[ls(x)] ^= 1 ; rev[rs(x)] ^= 1 ; rev[x] = 0 ;
}
inline void rotate(int x) {
  int y = fa[x] , z = fa[y] ;
  int k = getr(x) , w = ch[x][k ^ 1] ;
  ch[y][k] = w ; fa[w] = y ;
  if(! isroot(y)) ch[z][getr(y)] = x ;
  fa[x] = z ; ch[x][k ^ 1] = y ; fa[y] = x ;
  pushup(x) ; pushup(y) ;
}
inline void pushall(int x) { if(! isroot(x)) pushall(fa[x]) ; pushr(x) ; }
inline void splay(int x) {
  pushall(x) ;
  while(! isroot(x)) {
    int y = fa[x] , z = fa[y] ;
    if(! isroot(y)) rotate((ls(fa[x]) == x) ^ (ls(fa[y]) == y) ? x : y) ;
    rotate(x) ;
  } pushup(x) ;
}
inline void access(int x) { for( int tp = 0 ; x ; x = fa[tp = x]) splay(x) , rs(x) = tp , pushr(x) ; }
inline void makeroot(int x) { access(x) ; splay(x) ; rev[x] ^= 1 ; }
inline void split(int x , int y) { makeroot(x) ; access(y) ; splay(y) ; }
inline int findroot(int x) { access(x) ; splay(x) ; while(ls(x)) pushr(x) , x = ls(x) ; return x ; }
inline bool chk(int x , int y) { return findroot(x) == findroot(y) ; }
inline void link(int x , int y) { makeroot(x) ; fa[x] = y ; }

signed main() {
  n = read() ;
  for(register int i = 1 ; i <= n ; i ++) val[i] = read() ;
  for(register int t = read() ; t -- ; ) {
    char op[20] ; scanf("%s" , op + 1) ;
    int x = read() , y = read() ;
    if(op[1] == 'p') splay(x) , val[x] = y ;
    if(op[1] == 'b') { if(chk(x , y)) puts("no") ;
      else puts("yes") , link(x , y) ;
    }
    if(op[1] == 'e') {
      if(! chk(x , y)) puts("impossible") ;
      else split(x , y) , printf("%d\n" , sum[y]) ;
    }
  }
  return 0 ;
}

[SDOI2008]洞穴勘测

#include<bits/stdc++.h>
using namespace std ;
#define int long long
#define fi first
#define se second
#define pb push_back
inline int read() {
	register int x = 0 , f = 1 ;
	register char c = getchar() ;
	for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
	for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
	return x * f ;
}
template < typename T > inline bool cmax(T & x , T y) {
	return x < y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cmin(T & x , T y) {
	return x > y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cabs(T & x) {
	return x > 0 ? 1 : (x = - x) , 0 ;
}
inline int QP(int x , int y , int Mod) {
	int ans = 1 ;
	for( ; y ; y >>= 1 , x = (x * x) % Mod)
		if(y & 1) ans = (ans * x) % Mod ;
	return ans ;
}
int n , m ;
const static int N = 3e5 + 10 ;
int val[N] ;
class LCT {
public :
	int ch[N][2] ;  int fa[N] , sum[N] , rev[N] ;
	#define ls(x) ch[x][0]
	#define rs(x) ch[x][1]
	inline void push_up(int x) { sum[x] = sum[ls(x)] ^ sum[rs(x)] ^ val[x] ; }
	inline void rever(int x) { swap(ls(x) , rs(x)) ; rev[x] ^= 1 ; }
	inline void push_down(int x) { if(rev[x]) {if(ls(x)) rever(ls(x)) ; if(rs(x)) rever(rs(x)) ; rev[x] = 0 ; } }
	inline bool isroot(int x) { return ls(fa[x]) != x && rs(fa[x]) != x ; }
	inline void rotate(int x) {
		int fx = fa[x] , fy = fa[fx] , rs = (x == rs(fa[x])) , mus = ch[x][! rs] ;
		if(! isroot(fx)) ch[fy][fx == rs(fy)] = x ;
		ch[x][! rs] = fx ; ch[fx][rs] = mus ;
		if(mus) fa[mus] = fx ; fa[x] = fy  , fa[fx] = x ;
		push_up(fx) , push_up(x) ;
	}
	inline void pushall(int x) { if(! isroot(x)) pushall(fa[x]) ; push_down(x) ; }
	inline void splay(int x) {
		pushall(x) ;
		while(! isroot(x)) {
			int fx = fa[x] , fy = fa[fx] ;
			if(! isroot(fx)) rotate(((ls(fx) == x) ^ (ls(fy) == fx)) ? x : fx) ;
			rotate(x) ;
		}
	}
	inline void access(int x) { for(int tp = 0 ; x ; tp = x , x = fa[tp]) splay(x) , rs(x) = tp , push_up(x) ;}
	inline void make_root(int x) { access(x) ; splay(x) ; rever(x) ; }
	inline int find_root(int x){ access(x) ; splay(x) ; while(ls(x)) push_down(x) , x = ls(x) ; splay(x) ; return x ; }
	inline void split(int x , int y) { make_root(x) ; access(y) ; splay(y) ; }
	inline void cut(int x , int y) { make_root(x) ; if(find_root(y) == x && fa[y] == x && ! ls(y)) fa[y] = rs(x) = 0 , push_up(x) ; }
	inline void link(int x , int y) { make_root(x) ; if(find_root(y) != x) fa[x] = y ; }
} lct ;
inline int getopt() {
	register char c = getchar() ;
	string s = "" ;
	while(isspace(c)) c = getchar() ;
	while(! isspace(c)) s += c , c = getchar() ;
	if(s == "Connect") return 1 ;
	if(s == "Destroy") return 2 ;
	if(s == "Query") return 3 ;
}
signed main() {
	n = read() , m = read() ;
	for(register int i = 1 ; i <= m ; i ++) {
		int opt = getopt() ;
		int u = read() , v = read() ;
		if(opt == 1) lct.link(u , v) ;
		if(opt == 2) lct.cut(u , v) ;
		if(opt == 3) puts(lct.find_root(u) == lct.find_root(v) ? "Yes" : "No") ;
	}
	return 0 ;
}

[ZJOI2012]网络

因为颜色不超过20种所以20个LCT不断删边加边就可以了……边用map存一下

#include<bits/stdc++.h>
using namespace std ;
#define int long long
#define fi first
#define se second
#define pb push_back
inline int read() {
	register int x = 0 , f = 1 ;
	register char c = getchar() ;
	for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
	for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
	return x * f ;
}
template < typename T > inline bool cmax(T & x , T y) {
	return x < y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cmin(T & x , T y) {
	return x > y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cabs(T & x) {
	return x > 0 ? 1 : (x = - x) , 0 ;
}
inline int QP(int x , int y , int Mod) {
	int ans = 1 ;
	for( ; y ; y >>= 1 , x = (x * x) % Mod)
		if(y & 1) ans = (ans * x) % Mod ;
	return ans ;
}
int  n , m , c , k ;
const int N = 1e4 + 10 ;
int val[N] ;
class LCT {
	public :
	#define ls(x) ch[x][0]
	#define rs(x) ch[x][1]
	int fa[N] , ch[N][2] , rev[N] , cnt[N] , mx[N] ; int s[N] ; int top ;
	inline bool isroot(int x) { return ls(fa[x]) != x && rs(fa[x]) != x ; }
	inline void pushup(int x){mx[x]=val[x];
		if(ls(x)) cmax(mx[x],mx[ls(x)]);
		if(rs(x)) cmax(mx[x],mx[rs(x)]);
	}
	inline void pushdown(int x){
		if(x&&rev[x]){
			swap(ls(x),rs(x));
			rev[ls(x)]^=1,rev[rs(x)]^=1;
			rev[x]=0;
		}
	}
	inline void rotate(int x){
		int y=fa[x],z=fa[y],d=rs(y)==x;
		if(!isroot(y)) ch[z][rs(z)==y]=x;
		fa[x]=z;fa[y]=x;fa[ch[x][d^1]]=y,ch[y][d]=ch[x][d^1];ch[x][d^1]=y;
		pushup(y);
	}
	// inline void pushall(int x){if(!isroot(x))pushall(fa[x]);pushdown(x);}
	inline void splay(int x){
		// pushall(x);
		s[top=1]=x;
		for(int i=x;!isroot(i);i=fa[i])s[++top]=fa[i];
		while(top)pushdown(s[top--]);
		for(int y=fa[x],z=fa[y];!isroot(x);y=fa[x],z=fa[y]){
			if(!isroot(y))rotate((rs(y)==x)^(rs(z)==y)?x:y);
				rotate(x);
		}pushup(x);
		return ;
	}
	inline void access(int x){
		for(register int y = 0; x ; x = fa[y=x])
			splay(x),rs(x)=y,pushup(x);
		return ;
	}
	inline void makeroot(int x){ access(x);splay(x);rev[x]^=1;}
	inline void split(int x,int y){makeroot(x);access(y);splay(y);}
	inline void link(int x,int y){++ cnt[x] , ++ cnt[y] , makeroot(x),fa[x]=y;splay(x);}
	inline void cut(int x,int y){--cnt[x],--cnt[y],split(x,y),fa[x]=ls(y)=0,pushup(y);}
	inline int findroot(int x){access(x),splay(x),pushdown(x);while(ls(x))pushdown(x=ls(x));return x;}
	inline int query(int x,int y){split(x,y);return mx[y];}
} ;
LCT lct[15] ;
struct node{
	int u,v;
	inline bool operator <(const node & x) const {
		return u < x.u || (u == x.u && v < x.v) ;
	}
} ; map < node , int > mp ;
signed main() {
	n = read() , m = read() , c = read() ,k = read();
	for(register int i = 1 ; i <= n ; i ++) val[i] = read() ;
	for(register int i = 1 ; i <= m ; i ++) {
		int u = read() , v = read() , w = read() ;
		node edge1 = {u,v};
		node edge2 = {v,u};
		mp[edge1]=mp[edge2]=w;
		lct[w].link(u,v);
	}
	while(k -- ) {
		int opt = read() ;
		if(opt == 0) {
			int x = read() , w = read() ;
			val[x] = w ;
			for(register int i = 0 ; i < c ; i ++)
				lct[i].splay(x) ;
		}
		if(opt == 1) {
			int u = read(),v=read(),w = read() ;
			node edge1 = {u , v} ;
			node edge2 = {v , u} ;
			if(! mp.count(edge1)) { puts("No such edge.") ; continue ;}
			int x = mp[edge1] ;
			if(x == w) { puts("Success.") ; continue ;}
			if(lct[w].cnt[u]>=2 || lct[w].cnt[v]>=2) {
				puts("Error 1.") ;
				continue ;
			}
			if(lct[w].findroot(u) == lct[w].findroot(v)){
				puts("Error 2.") ;
				continue ;
			}
			puts("Success.");
			lct[x].cut(u , v) ;
			lct[w].link(u , v);
			mp[edge1]=mp[edge2]=w;
		}
		if(opt == 2){
			int w = read() , u = read() , v = read() ;
			if(lct[w].findroot(u) != lct[w].findroot(v)) {
				puts("-1") ;
				continue ;
			}
			printf("%lld\n" , lct[w].query(u,v)) ;
		}
	}
	return 0 ;
}

[SDOI2017]树点涂色

[AH2017/HNOI2017]单旋

这题有点烦 不太想讲…

每次单旋只会取maxormin,那么手玩发现,这样树的形态基本不变!

那么我们可以直接把x提上去,这是手动维护Spaly的形态,

我们想怎么统计答案呢?暴力跳显然是会T的,这里实质是查询点到根的距离,

可以考虑使用LCT维护,这样就直接查询点到根的路径长度就可以了

然后直接无脑set维护一下就可以了

// Isaunoya
#include<bits/stdc++.h>
using namespace std ;
#define int long long
#define fi first
#define se second
#define pb push_back
inline int read() {
  register int x = 0 , f = 1 ;
  register char c = getchar() ;
  for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
  for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
  return x * f ;
}
template < typename T > inline bool cmax(T & x , T y) {
	return x < y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cmin(T & x , T y) {
	return x > y ? (x = y) , 1 : 0 ;
}
inline int QP(int x , int y , int Mod){ int ans = 1 ;
  for( ; y ; y >>= 1 , x = (x * x) % Mod)
    if(y & 1) ans = (ans * x) % Mod ;
  return ans ;
}
const int N = 1e6 + 10 ;
int ch[N][2] ;
int tot = 0 ;
int fa[N] , sub[N] , rt = 0 , cnt = 0 ;
bool rev[N] ; int size[N] , f[N] ;
int c[N][2] ;
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
inline bool isroot(int x) { return ls(fa[x]) != x && rs(fa[x]) != x ; }
inline void pushup(int x) { size[x] = size[ls(x)] + size[rs(x)] + 1 ; }
inline void pushr(int x) { if(! rev[x]) return ; rev[x] ^= 1 ; rev[ls(x)] ^= 1 ; rev[rs(x)] ^= 1 ; swap(ls(x) , rs(x)) ; }
inline void rotate(int x) {
  int y = fa[x] , z = fa[y] ;
  int qwq = rs(y) == x ? 1 : 0 ;
  if(! isroot(y)) ch[z][rs(z) == y] = x ;
  fa[x] = z ; fa[y] = x ; fa[ch[x][qwq ^ 1]] = y ; ch[y][qwq] = ch[x][qwq ^ 1] ;
  ch[x][qwq ^ 1] = y ; pushup(y) ; pushup(x) ;
}
inline void pushall(int x) { if(! isroot(x)) pushall(fa[x]) ; pushr(x) ; }
inline void splay(int x) {
  pushall(x) ;
  while(! isroot(x)) {
    int y = fa[x] , z = fa[y] ;
    if(! isroot(y)) rotate((ls(y) == x) ^ (ls(z) == y) ? x : y) ;
    rotate(x) ;
  }
}
inline void access(int x) {
  for( int tp = 0 ; x ; tp = x , x = fa[x]) splay(x) , rs(x) = tp , pushup(x) ;
}
inline void makeroot(int x) { access(x) ; splay(x) ; rev[x] ^= 1 ; }
inline void link(int x, int y) { if(! x || ! y) return ; makeroot(x) ; fa[x] = y ; }
inline void cut(int x , int y) { if(! x || ! y) return ; makeroot(x) ; access(y) ; splay(y) ; ls(y) = fa[x] = 0 ; pushup(x) ; pushup(y) ;  }
inline int query(int x) { makeroot(rt) ; access(x) ; splay(x) ; return size[x] ; }

set < int > s ;
typedef set <int> :: iterator IT ;
struct node { int flg , kk ; } a[N] ;
signed main() {
  int t = read() ; s.insert(INT_MAX) ; s.insert(INT_MIN) ;
  for( int i = 1 ; i <= t ; i ++ ) {
    a[i].flg = read() ; if(a[i].flg == 1) {
      a[i].kk = read() ;
      sub[++ tot] = a[i].kk ;
    }
  }
  sort(sub + 1 , sub + tot + 1) ;
  tot = unique(sub + 1 , sub + tot + 1) - sub - 1 ;
  for( int i = 1 ; i <= t ; i ++) {
    if(a[i].flg == 1) {
      a[i].kk = lower_bound(sub + 1 , sub + tot + 1 , a[i].kk) - sub ;
      if(! cnt) { ++ cnt ; rt = a[i].kk ; s.insert(rt) ; printf("1\n") ; continue ; }
      else {
        IT it = s.upper_bound(a[i].kk) ;
        int nxt = * it , dep = 0 , x ; -- it ;
        int pre = * it ;
        if(pre != INT_MIN) { int now = query(pre) ; if(now > dep) dep = now , x = pre ; }
        if(nxt != INT_MAX) { int now = query(nxt) ; if(now > dep) dep = now , x = nxt ; }
        printf("%lld\n" , dep + 1) ; c[x][a[i].kk > x] = a[i].kk ; f[a[i].kk] = x ;
        ++ cnt ; link(x , a[i].kk) ; s.insert(a[i].kk) ;
      }
    }
    if(a[i].flg == 2) {
      if(cnt == 1) { puts("1") ; continue ; }
      IT it = s.begin() ; ++ it ; int x = * it , y = c[x][1] , z = f[x] , k = query(x) ;
      if(rt != x) { cut(x , z) ; cut(x , y) ; link(x , rt) , link(z , y) ; f[x] = 0 ; c[x][1] = rt ; f[rt] = x ; rt = x ; c[z][0] = y ; f[y] = z ; }
      printf("%lld\n", k) ;
    }
    if(a[i].flg == 3) {
      if(cnt == 1) { puts("1") ; continue ; }
      IT it = s.end() ; -- it , -- it ; int x = * it , y = c[x][0] , z = f[x] , k = query(x) ;
      if(rt != x) { cut(x , z) ; cut(x , y) ; link(x , rt) ; link(z , y) ; f[x] = 0 ; c[x][0] = rt ; f[rt] = x ; rt = x ; c[z][1] = y ; f[y] = z ; }
      printf("%lld\n" , k) ;
    }
    if(a[i].flg == 4) {
      if(cnt == 1) { -- cnt ; puts("1") ; s.erase(s.find(rt)) ; rt = 0 ;continue ; }
      IT it = s.begin() ; ++ it ; int x = * it , y = c[x][1] , z = f[x] , k = query(x) ;
      cut(x , z) ; cut(x , y) ; link(y , z) ; cnt -- ; s.erase(s.find(x)) ;
      if(x == rt) { rt = y ; }
      c[x][0] = c[x][1] = f[x] = 0 ; c[z][0] = y ; f[y] = z ;
      printf("%lld\n" , k) ;
    }
    if(a[i].flg == 5) {
      if(cnt == 1) { cnt -- ; puts("1") ; s.erase(s.find(rt)) ; rt = 0 ; continue ; }
      IT it = s.end() ; -- it ; -- it ; int x = * it , y = c[x][0] , z = f[x] , k = query(x) ;
      cut(x , z) ; cut(x , y) ; link(y , z) ; cnt -- ; s.erase(s.find(x)) ;
      printf("%lld\n" , k) ;
      if(x == rt) { rt = y ; }
      c[x][0] = c[x][1] = f[x] = 0 ; c[z][1] = y ; f[y] = z ;
    }
  }
	return 0 ;
}

连环病原体

题意大概是这样，有m条无向边按输入顺序标号，如果一段区间\([l,r]\)上的无向边包含环就称区间\([l,r]\)是“加强区间”，求每条边分别在多少个“加强区间”内。

#include<bits/stdc++.h>

typedef long long LL ;
#define int long long
using namespace std ;
template < typename T > inline void read(T & x) { x = 0 ; int f = 1 ;
  register char c = getchar() ;
  while(! isdigit(c)) {
    if(c == '-') f = -1 ;
    c = getchar() ;
  }
  while(isdigit(c)) { x = (x << 1) + (x << 3) + (c & 15) ; c = getchar() ; }
  x *= f ; return ;
}
const int N = 4e5 + 10 ;
struct Edge { int u , v ; } e[N] ;
template < > inline void read < Edge > (Edge & x) {
  read(x.u) ; read(x.v) ; return void() ;
}

template < typename T > inline void print(T x) {
  if(x == 0) return putchar('0') , void() ;
  static int st[105] ;
  if(x < 0) putchar('-') , x = -x ;
  int tp = 0 ;
  while(x) st[++ tp] = x % 10 , x /= 10 ;
  while(tp) putchar(st[tp --] + '0') ;
  return ;
}

template < typename T > inline void sort(vector < T > & v) { sort(v.begin() , v.end()) ; }
template < typename T > inline void unique(vector < T > & v) { v.erase(unique(v.begin() , v.end()) , v.end()) ; }
inline int getdigit() {
  register char c = getchar() ;
  while(! isdigit(c)) c = getchar() ;
  return c - '0' ;
}
inline char getc() {
  register char c = getchar() ;
  while(! (c >= 'A' && c <= 'Z')) c = getchar() ;
  return c ;
}

inline int gcd(int x , int y) { return y == 0 ? x : gcd(y , x % y) ; }

const static LL Mod = LLONG_MAX ;

template < typename T , typename TT > inline void Add(T & x , TT y , T Mod = Mod) { x += y ; if(x >= Mod) x -= Mod ; }
template < typename T , typename TT > inline void Del(T & x , TT y , T Mod = Mod) { x -= y ; if(x < 0) x += Mod ; }

int n , m ;
int del[N] , del2[N] ;

template < typename T >
class LCT {
  public :
  int ch[N][2] , fa[N] ;
  int rev[N] , sum[N] ;
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
  inline bool isroot(int x) { return ls(fa[x]) != x && rs(fa[x]) != x ; }
  inline bool getr(int x) { return rs(fa[x]) == x ; }
  inline void pushup(int x) { return void() ; }
  inline void rever(int x) { rev[x] ^= 1 ; swap(ls(x) , rs(x)) ; }
  inline void pushr(int x) {
    if(! rev[x]) return ;
    rev[x] ^= 1 ;
    if(ls(x)) rever(ls(x)) ;
    if(rs(x)) rever(rs(x)) ;
    return void() ;
  }
  inline void rotate(int x) {
    int y = fa[x] , z = fa[y] ; int k = getr(x) ;
    if(! isroot(y)) ch[z][getr(y)] = x ;
    fa[x] = z ;
    ch[y][k] = ch[x][k ^ 1] ;
    fa[ch[y][k]] = y ;
    ch[x][k ^ 1] = y ;
    fa[y] = x ;
    // pushup(y) ; pushup(x) ;
    return void() ;
  }
  inline void pushall(int x) { if(! isroot(x)) pushall(fa[x]) ; return pushr(x) , void() ; }
  inline void splay(int x) {
    pushall(x) ;
    while(! isroot(x)) {
      int y = fa[x] , z = fa[y] ;
      if(! isroot(y)) rotate((getr(x) ^ getr(y)) ? x : y) ;
      rotate(x) ;
    }
    return void() ;
  }
  inline void acess(int x) { for( int tp = 0 ; x ; x = fa[tp = x]) splay(x) , rs(x) = tp ; return void() ; }
  inline void makeroot(int x) { acess(x) ; splay(x) ; rever(x) ; }
  inline int findroot(int x) { acess(x) ; splay(x) ; while(ls(x)) pushr(x) , x = ls(x) ; splay(x) ; return x ; }
  inline void link(int x , int y) { makeroot(x) ; fa[x] = y ; }
  inline void cut(int x , int y) {makeroot(x) ; acess(y) ; splay(y) ; if((ls(y) != x) && (! rs(ls(y)))) return void() ; fa[x] = ls(y) = 0 ; }
  // inline void query(int x , int y) { makeroot(x) ; acess(y) ; splay(y) ; return void() ; }
} ;

LCT < int > t ;

inline void solve(int l , int r , int _h , int _t) {
  if(l > r) return void() ;
  del[l ++] += _h ;
  del[++ r] -= _h ;
  del2[l] += _t ;
  del2[r] -= _t ;
  return void() ;
}
signed main() {
  // freopen("testdata.in" , "r" , stdin) ;
  read(m) ;
  for(register int i = 1 ; i <= m ; i ++) read(e[i]) ;
  int r = 1 ;
  for(register int l = 1 ; l <= m ; l ++) {
    while(r <= m) {
      int u = e[r].u , v = e[r].v ;
      if(t.findroot(u) == t.findroot(v)) { solve(l , r , m - r + 1 , 0) ; solve(r + 1 , m , m - r , - 1) ; break ; }
      else { t.link(u , v) ; } ++ r ;
    }
    t.cut(e[l].u , e[l].v) ;
  }
  int x = 0 , y = 0 ;
  for(register int i = 1 ; i <= m ; i ++) {
    x += del[i] , y += del2[i] , x += y ;
    print(x) , putchar(32) ;
  }
  return 0 ;
}

LCT 可以维护动态MST（动态最小生成树）

指最小生成树 思路大概是

如果不连通直接加 link一下的…

如果连通split提上去 然后判断大小关系来删边断边 如果满足最优性 则不变…

[NOI2014]魔法森林

#include<bits/stdc++.h>
using namespace std ;
#define int long long
#define fi first
#define se second
#define pb push_back
inline int read() {
	register int x = 0 , f = 1 ;
	register char c = getchar() ;
	for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
	for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
	return x * f ;
}
template < typename T > inline bool cmax(T & x , T y) {
	return x < y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cmin(T & x , T y) {
	return x > y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cabs(T & x) {
	return x > 0 ? 1 : (x = - x) , 0 ;
}
inline int QP(int x , int y , int Mod) {
	int ans = 1 ;
	for( ; y ; y >>= 1 , x = (x * x) % Mod)
		if(y & 1) ans = (ans * x) % Mod ;
	return ans ;
}
int n , m  ;
const int N = 1e5 + 10 ;
struct node {
  int u , v , w , w2 ;
  inline bool operator <(const node & x ) const {
    return w < x.w ;
  }
} e[N] ;
int l[N] , r[N] ;
int f[N] ;
int idx ;
inline int find(int x) { return x == f[x] ? x : f[x] = find(f[x]) ;}
inline void merge(int x , int y) { return f[find(x)] = find(y) , void() ;}
class LCT {
public :
  int fa[N] , ch[N][2] , tag[N] ;
  int w[N] , id[N] ;
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
  inline bool getr(int x) { return rs(fa[x]) == x ; }
  inline bool isroot(int x) { return ls(fa[x]) != x && rs(fa[x]) != x ; }

  inline void pushr(int x) { tag[x] ^= 1 ; swap(ls(x) , rs(x)) ; }
  inline void pushup(int x) { id[x] = x ; if(w[id[ls(x)]] > w[id[x]]) id[x] = id[ls(x)] ; if(w[id[rs(x)]] > w[id[x]]) id[x] = id[rs(x)] ; }
  inline void pushdown(int x) { if(tag[x]) { tag[x] = 0 ; if(ls(x)) pushr(ls(x)) ; if(rs(x)) pushr(rs(x)) ; }}

  inline void rotate(int x) { int y = fa[x] , z = fa[y] , k = getr(x) ;
    if(!isroot(y)) ch[z][getr(y)] = x ;
    fa[x] = z ; fa[y] = x ; fa[ch[x][k ^ 1]] = y ; ch[y][k] = ch[x][k ^ 1] ; ch[x][k ^ 1] = y ;
    pushup(y) ;
  }
  inline void pushall(int x) { if(! isroot(x)) pushall(fa[x]) ; pushdown(x) ; }
  inline void splay(int x) {
    pushall(x) ;
    while(! isroot(x)) {
      int y = fa[x] ;
      if(! isroot(y)) rotate(getr(x) ^ getr(y) ? x : y) ;
        rotate(x) ;
    } pushup(x) ;
  }
  inline void access(int x) { for( int tp = 0 ; x ; rs(x) = tp , tp = x , x = fa[tp]) splay(x) ; }
  inline void makeroot(int x) { access(x) ; splay(x) ; pushr(x) ; }
  inline void split(int x , int y) { makeroot(x) ; access(y) ; splay(y) ; }
  inline int findroot(int x) { access(x) ; splay(x) ; while(ls(x)) x = ls(x) ; splay(x) ; return x ; }
  inline void link(int x , int y) { makeroot(x) ; if(findroot(y) != x) fa[x] = y ; }
  inline void cut(int x , int y) { makeroot(x) ; access(y) ; splay(y) ; if(ls(y) == x) ls(y) = fa[x] = 0 , pushup(y) ;}
  inline int query(int x , int y) {
		if(findroot(x) != findroot(y)) return INT_MAX ;
		split(x , y) ;
		return w[id[y]] ;
	}
	inline void Merge(int x , int y , int k) {
		if(findroot(x) ^ findroot(y)) { w[++ idx] = k ; link(l[idx] = x , idx) ; link(r[idx] = y , idx) ; return ; }
		split(x , y) ;
		int s = id[y] ;
		if(w[s] <= k) return ;
		cut(s , l[s] ) ;
		cut(s , r[s] ) ;
		w[s] = k ;
		link(l[s] = x , s) ;
		link(r[s] = y , s) ;
	}
} lct ;
signed main() {
	// freopen("testdata.in" , "r" , stdin) ;
	// freopen("testdata2.out" , "w" , stdout) ;
  n = read() , m = read() ;
  for(register int i = 1 ; i <= m ; i ++) {
    int u = read() , v = read() , w = read() , w2 = read() ;
    e[i] = {u , v , w , w2} ;
  }
  sort(e + 1 , e + m + 1) ;
  int ans = INT_MAX ;
  idx = n ;
	for(register int i = 1 ; i <= n ; i ++) f[i] = i ;
  for(register int i = 1 ; i <= m ; i ++) {
		lct.Merge(e[i].u , e[i].v , e[i].w2) ;
		cmin(ans , e[i].w + lct.query(1 , n)) ;
	}
	if(ans == INT_MAX) ans = -1 ;
	printf("%lld\n" , ans) ;
	return 0 ;
}

[WC2006]水管局长

每次删边的LCT不太好维护MST

所以每次考虑倒着

离线先kruskal跑出来（为了复杂度）

然后再一步步动态加边 最后倒着输出（

#include<bits/stdc++.h>
using namespace std ;
// #define int long long
#define fi first
#define se second
#define pb push_back
inline int read() {
	register int x = 0 , f = 1 ;
	register char c = getchar() ;
	for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
	for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
	return x * f ;
}
template < typename T > inline bool cmax(T & x , T y) {
	return x < y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cmin(T & x , T y) {
	return x > y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cabs(T & x) {
	return x > 0 ? 1 : (x = - x) , 0 ;
}
inline int QP(int x , int y , int Mod) {
	int ans = 1 ;
	for( ; y ; y >>= 1 , x = (x * x) % Mod)
		if(y & 1) ans = (ans * x) % Mod ;
	return ans ;
}
int n , m , q ;
int id ;
const int N = 3e5 + 5 ;
int l[N] , r[N] ;
struct node {
  int u , v , w ;
  inline bool operator < (const node& x ) const{ return w < x.w ; }
} e[1000005] ;
int f[100005] ;
map < int , int > p[100005] ;
struct que {
  int op , x , y , w ;
} qs[100005] ;
class LCT {
public :
  int fa[N] , ch[N][2] , tag[N] ;
  pair < int , int > val[N] , mn[N] ;
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
  inline bool getr(int x) { return rs(fa[x]) == x ; }
  inline bool isroot(int x) { return ls(fa[x]) != x && rs(fa[x]) != x ; }

  inline void pushr(int x) { tag[x] ^= 1 ; swap(ls(x) , rs(x)) ; }
  inline void pushup(int x) { mn[x] = max(val[x] , max(mn[ls(x)] , mn[rs(x)])) ; }
  inline void pushdown(int x) { if(tag[x]) { tag[x] = 0 ; if(ls(x)) pushr(ls(x)) ; if(rs(x)) pushr(rs(x)) ; }}

  inline void rotate(int x) { int y = fa[x] , z = fa[y] , k = getr(x) ;
    if(!isroot(y)) ch[z][getr(y)] = x ;
    fa[x] = z ; fa[y] = x ; fa[ch[x][k ^ 1]] = y ; ch[y][k] = ch[x][k ^ 1] ; ch[x][k ^ 1] = y ;
    pushup(y) ;
  }
  inline void pushall(int x) { if(! isroot(x)) pushall(fa[x]) ; pushdown(x) ; }
  inline void splay(int x) {
    pushall(x) ;
    while(! isroot(x)) {
      int y = fa[x] ;
      if(! isroot(y)) rotate(getr(x) ^ getr(y) ? x : y) ;
        rotate(x) ;
    } pushup(x) ;
  }
  inline void access(int x) { for( int tp = 0 ; x ; rs(x) = tp , tp = x , x = fa[tp]) splay(x) ; }
  inline void makeroot(int x) { access(x) ; splay(x) ; pushr(x) ; }
  inline void split(int x , int y) { makeroot(x) ; access(y) ; splay(y) ; }
  inline int findroot(int x) { access(x) ; splay(x) ; while(ls(x)) x = ls(x) ; splay(x) ; return x ; }
  inline void link(int x , int y) { makeroot(x) ; if(findroot(y) != x) fa[x] = y ; }
  inline void cut(int x , int y) { makeroot(x) ; access(y) ; splay(y) ; if(ls(y) == x) ls(y) = fa[x] = 0 , pushup(y) ;}
  inline pair < int , int > query(int x , int y) { split(x , y) ; return mn[y] ; }
} lct ;

inline int find(int x) { return x == f[x] ? x : f[x] = find(f[x]) ;}
signed main() {
  n = read() ; m = read() ; q = read() ;
  for(register int i = 1 ; i <= m ; i ++) {
    int u = read() , v = read() , w = read() ;
    if(u > v) swap(u , v) ;
    e[i] = {u , v , w} ;
    p[e[i].u][e[i].v] = e[i].w ;
  }
  for(register int i = 1 ; i <= q ; i ++) {
    qs[i].op = read() ;
    qs[i].x = read() ;
    qs[i].y = read() ;
    if(qs[i].x > qs[i].y) swap(qs[i].x , qs[i].y) ;
    if(qs[i].op == 2) {
      qs[i].w = p[qs[i].x][qs[i].y] ;
      p[qs[i].x].erase(qs[i].y) ;
    }
  }
  sort(e + 1 , e + m + 1) ;
  for(register int i = 1 ; i <= n ; i ++) f[i] = i ;
  id = n ;
  for(register int i = 1 ; i <= m ; i ++) {
    int u = e[i].u , v = e[i].v ;
    if(! p[u].count(v)) continue ;
    u = find(u) , v = find(v) ;
    if(u ^ v) {
      f[v] = u ;
      ++ id ;
      lct.val[id] = lct.mn[id] = make_pair(e[i].w , id) ;
      lct.link(id , l[id] = e[i].u) ;
      lct.link(id , r[id] = e[i].v) ;
    }
  }
  static int st[100005] , top = 0 ;
  for(register int i = q ; i ; -- i) {
    if(qs[i].op == 1) st[++ top] = (qs[i].x ^ qs[i].y) ? lct.query(qs[i].x , qs[i].y).first : 0 ;
    else {
      int x = qs[i].x , y = qs[i].y ;
      pair < int , int > d = lct.query(x , y) ;
      if(d.fi <= qs[i].w) continue ;
      int t = d.se ;
      lct.cut(l[t] , t) ;
      lct.cut(r[t] , t) ;
      ++ id ;
      lct.val[id] = lct.mn[id] = make_pair(qs[i].w , id) ;
      lct.link(l[id] = x , id) ;
      lct.link(r[id] = y , id) ;
    }
  }
  while(top) printf("%d\n" , st[top --]) ;
	return 0 ;
}

[USACO18FEB]New Barns

大概题意就是合并两个连通块 查询连通块内点到其他点的最大距离 对于这道题更简单 因为每次只有一个点和一个连通块合并 所以直接求两次距离即可 每个点的权值设为1 split后上面那个点的sum-1即为距离

#include<bits/stdc++.h>
using namespace std ;
#define int long long
#define fi first
#define se second
#define pb push_back
inline int read() {
	register int x = 0 , f = 1 ;
	register char c = getchar() ;
	for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
	for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
	return x * f ;
}
template < typename T > inline bool cmax(T & x , T y) {
	return x < y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cmin(T & x , T y) {
	return x > y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cabs(T & x) {
	return x > 0 ? 1 : (x = - x) , 0 ;
}
inline int QP(int x , int y , int Mod) {
	int ans = 1 ;
	for( ; y ; y >>= 1 , x = (x * x) % Mod)
		if(y & 1) ans = (ans * x) % Mod ;
	return ans ;
}
int q , m = 0 ;
const int N = 1000000 + 5 ;
int val[N] ;
class LCT {
	public :
	int ch[N][2] ; int fa[N] ; int size[N] ; int rev[N] ;

#define ls(x) ch[x][0]
#define rs(x) ch[x][1]

	inline void pushup(int rt) { size[rt] = size[ls(rt)] + size[rs(rt)] + 1 ; }

	inline void pushr(int rt) { rev[rt] ^= 1 ;swap(ls(rt) , rs(rt)) ; }

	inline void pushdown(int rt) {
		if(! rev[rt]) return ;
		rev[rt] ^= 1 ;
		if(ls(rt)) pushr(ls(rt)) ;
		if(rs(rt)) pushr(rs(rt)) ;
	}

	inline bool getr(int x) { return rs(fa[x]) == x ; }
	inline bool isroot(int x) { return ls(fa[x]) != x && rs(fa[x]) != x ; }

	inline void rotate(int x) {
		int y = fa[x] , z = fa[y] , rs = getr(x) , grs = getr(y) ;
		int son = ch[x][rs ^ 1] ;
		if(! isroot(y)) ch[z][grs] = x ;
		ch[y][rs] = son ; ch[x][rs ^ 1] = y ;
		fa[x] = z ; fa[y] = x ;
		if(son) fa[son] = y ; pushup(y) ;
	}

	inline void pushall(int x) { if(! isroot(x)) pushall(fa[x]) ; pushdown(x) ; }
	inline void splay(int x) {
		pushall(x) ;
		while(! isroot(x)) {
			if(! isroot(fa[x])) rotate(getr(fa[x]) ^ getr(x) ? x : fa[x]) ;
			rotate(x) ;
		} pushup(x) ;
	}

	inline void access(int x) { for(register int tp = 0 ; x ; tp = x , x = fa[tp]) splay(x) , rs(x) = tp , pushup(x) ; }
	inline void makeroot(int x) { access(x) ; splay(x) ;  pushr(x) ; }
	inline void split(int x , int y) { makeroot(y) ; access(x) ; splay(x) ; }

	inline void link(int x , int y) { if(! x || ! y || x == y) return ; split(x , y) ; fa[y] = x ; }
	inline void cut(int x , int y) { if(! x || ! y || x == y) return ; split(x , y) ; if(size[x] <= 2) ls(x) = fa[y] = 0 ;}
} lct ;

struct node{
	int u , v , w ;
} e[N] ;
int f[N] ;
inline int find(int x) { return x == f[x] ? x : f[x] = find(f[x]) ;}
inline int query(int x , int y) { lct.split(x , y) ; return lct.size[x] - 1 ;}

inline void Merge(int x , int y) {
	lct.link(x , y) ; f[x] = y = find(y) ;
	register int a = x , b = e[y].u , c = e[y].v , maxn = e[y].w , tmp ;
	tmp = query(a , b) ;
	if(cmax(maxn , tmp)) e[y].u = a , e[y].v = b ;
	tmp = query(a , c) ;
	if(cmax(maxn , tmp)) e[y].u = a , e[y].v = c ;
	tmp = query(b , c) ;
	if(cmax(maxn , tmp)) e[y].u = b , e[y].v = c ;
	e[y].w = maxn ;
}

inline int getopt() { register char c = getchar() ;
	while(c != 'Q' && c != 'B') c = getchar() ;
	return c == 'B' ;
}

signed main() {
	q = read() ;
	while(q --) {
		int opt = getopt() ;
		if(opt == 1) {
			int x = ++ m ;
			int y = read() ;
			e[x].u = e[x].v = x , f[x] = x ;
			if(~ y) Merge(x , y) ;
		}
		else {
			int x = read() , y = find(x) ;
			printf("%lld\n" , max(query(x , e[y].u) , query(x , e[y].v))) ;
		}
	}
	return 0 ;
}

LCT维护树的重心

首都

具体找法：类似树上二分，我们需要不断逼近树的重心的位置。记下lsum表示当前链中搜索区间左端点以左的子树大小，rsum表示右端点以右的。x的整个子树就表示了当前搜索区间，在中序遍历中x把搜索区间分成了左右两块（在Splay中对应x的左子树和右子树）。

如果x左子树的s加上lsum和x右子树的s加上rsum都不超过新树总大小的一半，那么x当然就是重心啦！当然，如果总大小是奇数，重心只会有一个，那就找到了。否则，因为必须编号最小，所以还要继续找下去。

当我们没有确定答案时，还要继续找下去，那么就要跳儿子了。x把整个链分成了左右两个部分，而重心显然会在大小更大的一部分中，这个也应该好证明。如果x左子树的s加上lsum小于x右子树的s加上rsum，那就跳右儿子继续找。这时候当前搜索区间减小了，搜索区间以外的部分增大了，lsum应该加上sz[x]+1。反之亦然。如果跳进了空儿子，那肯定所有情况都考虑完了，直接结束查找。

当然，重心找到了就还是要伸展一下，保证复杂度。

这一部分套用Splay的复杂度，是均摊\(O(\log N)\)的，总复杂度也就降到了\(O(N\log N)\)。

findroot实在很慢，于是可以写个并查集来维护每个点所在树的重心。

#include<bits/stdc++.h>

using namespace std ;
int n , m ;
const int N = 1e5 + 10 ;
const int INF = INT_MAX ;
int fa[N] , ch[N][2] , sz[N] , sum[N] , r[N] ;
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
inline bool isroot(int x) { return ls(fa[x]) != x && rs(fa[x]) != x ; }
inline bool getr(int x) { return rs(fa[x]) == x ; }
inline void pushup(int x) {
  sum[x] = sum[ls(x)] + sum[rs(x)] + sz[x] + 1 ;
}
inline void pushdown(int x) {
  if(! r[x]) return ;
  r[x] = 0 ; r[ls(x)] ^= 1 ; r[rs(x)] ^= 1 ;
  swap(ls(x) , rs(x)) ;
}
inline void rotate(int x) {
  int y = fa[x] , z = fa[y] , k = getr(x) , w = ch[x][k ^ 1] ;
  if(! isroot(y)) { ch[z][getr(y)] = x ; }
  fa[fa[fa[ch[ch[x][k ^ 1] = y][k] = w] = y] = x] = z ; pushup(y) ;
}
inline void pushall(int x) {
  if(! isroot(x)) pushall(fa[x]) ; pushdown(x) ;
}
inline void splay(int x) {
  pushall(x) ;
  while(! isroot(x)) {
    int y = fa[x] ;
    if(! isroot(y)) { rotate((getr(x) ^ getr(y)) ? x : y) ; }
    rotate(x) ;
  }
  pushup(x) ;
}
inline void access(int x) {
  for( int tp = 0 ; x ; x = fa[tp = x]) {
    splay(x) ;
    sz[x] += sum[rs(x)] ;
    sz[x] -= sum[rs(x) = tp] ;
    pushup(x) ;
  }
}
inline void makeroot(int x) {
  access(x) ; splay(x) ; r[x] ^= 1 ;
}
inline void split(int x , int y) {
  makeroot(x) ; access(y) ; splay(y) ;
}
inline void link(int x , int y){
  split(x , y) ; sz[fa[x] = y] += sum[x] ; pushup(y) ;
}
int f[N] ;
inline int find(int x) { return x == f[x] ? x : f[x] = find(f[x]) ; }
inline int upd(int x) {
  int l , r , j = sum[x] & 1 , Sum = sum[x] >> 1 ; int lsum = 0 , rsum = 0 ;
  int newp = INF , nowl = 0 , nowr = 0 ;
  while(x) {
    pushdown(x) ;
    nowl = sum[l = ls(x)] + lsum ;
    nowr = sum[r = rs(x)] + rsum ;
    if(nowl <= Sum && nowr <= Sum) {
      if(j) { newp = x ; break ; }
      else if(newp > x) { newp = x ; }
    }
    if(nowl < nowr) { lsum += sum[l] + sz[x] + 1 ; x = r ; }
    else { rsum += sum[r] + sz[x] + 1 ; x = l ; }
  }
  splay(newp) ;
  return newp ;
}
int ans = 0 ;
signed main() {
#ifdef _WIN64
  freopen("0.in" , "r" , stdin) ;
#endif
  ios :: sync_with_stdio(false) ;
  cin.tie(nullptr) ;
  cout.tie(nullptr) ;
  cin >> n >> m ;
  for(register int i = 1 ; i <= n ; i ++) { sum[i] = 1 ; f[i] = i ; ans ^= i ; }
  while(m --) {
    register char ch ; cin >> ch ;
    if(ch == 'A') {
      int x , y ; cin >> x >> y ;
      link(x , y) ;
      split(x = find(x) , y = find(y)) ;
      int z = upd(y) ;
      ans ^= x ^ y ^ z ;
      f[x] = f[y] = f[z] = z ;
    }
    if(ch == 'Q') {
      int x ; cin >> x ;
      cout << find(x) << '\n' ;
    }
    if(ch == 'X') {
      cin >> ch >> ch ;
      cout << ans << '\n' ;
    }
  }
}

最小差值生成树

给定一个标号为从 \(1\) 到 \(n\) 的、有 \(m\) 条边的无向图，求边权最大值与最小值的差值最小的生成树

要保证边权差最小，不妨假设当前边权为\(k\)，则此时我们需要最小边权最大。

所以可以按照边权排序。

类似于求最小生成树的方法，我们每次加边后都需要判一下连通性，如果联通就减去边权中最小值。

至于如何求出所有边权中的最小值，因为已经排序，所以有下标小的点其点权一定小。

所以我们可以用 \(flg\) 数组来标记那些点已经被标记，然后类似与队列的一个一个弹??

当然，需要统计答案的时候，还要判断\(id_{num}\)

num（合并次数）（当前联通块数量是否为1）是否为\(n-1\)

区别与最小生成树的模板，因为我们有编号小的点且为边的点其越小，所以我们可以这样写\(pushup\)

inline void pushup(int x) { id[x] = x ;
    if(id[ls(x)] > n && (id[x] <= n || id[x] > id[ls(x)]))id[x] = id[ls(x)] ;
    if(id[rs(x)] > n && (id[x] <= n || id[x] > id[rs(x)])) id[x] = id[rs(x)] ;
  }

// Isaunoya
#include<bits/stdc++.h>
using namespace std ;
#define int long long
#define fi first
#define se second
#define pb push_back
inline int read() {
  register int x = 0 , f = 1 ;
  register char c = getchar() ;
  for( ; ! isdigit(c) ; c = getchar()) if(c == '-') f = -1 ;
  for( ; isdigit(c) ; c = getchar()) x = (x << 1) + (x << 3) + (c & 15) ;
  return x * f ;
}
template < typename T > inline bool cmax(T & x , T y) {
	return x < y ? (x = y) , 1 : 0 ;
}
template < typename T > inline bool cmin(T & x , T y) {
	return x > y ? (x = y) , 1 : 0 ;
}
inline int QP(int x , int y , int Mod){ int ans = 1 ;
  for( ; y ; y >>= 1 , x = (x * x) % Mod)
    if(y & 1) ans = (ans * x) % Mod ;
  return ans ;
}

int n , m ;
const int N = 4e5 + 10 ;
const int M = 4e5 + 10 ;
struct node { int u , v , w ; } e[M << 1] ;
inline bool cmp(node x , node y) {
  return x.w < y.w ;
}
bool flg[M] ;
class LCT {
public :
  int fa[M] , id[M] ;
  bool rev[M] ;
  int ch[M][2] ;
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
  inline bool isroot(int x) { return ls(fa[x]) != x && rs(fa[x]) != x ; }
  inline void pushup(int x) { id[x] = x ;
    if(id[ls(x)] > n && (id[x] <= n || id[x] > id[ls(x)]))id[x] = id[ls(x)] ;
    if(id[rs(x)] > n && (id[x] <= n || id[x] > id[rs(x)])) id[x] = id[rs(x)] ;
  }
  inline void rever(int x) { if(! rev[x]) return ; rev[x] ^= 1 ; rev[ls(x)] ^= 1 ; rev[rs(x)] ^= 1 ; swap(ls(x) , rs(x)) ; }
  inline void rotate(int x) { int y = fa[x] , z = fa[y] ;
    int qwq = rs(y) == x ; fa[x] = z ;
    if(! isroot(y)) ch[z][rs(z) == y] = x ;
    fa[ch[x][qwq ^ 1]] = y ; ch[y][qwq] = ch[x][qwq ^ 1] ;
    fa[y] = x ; ch[x][qwq ^ 1] = y ;
    pushup(y) , pushup(x) ;
  }
  inline void pushall(int x) { if(! isroot(x)) pushall(fa[x]) ; rever(x) ; }
  inline void Splay(int x) { pushall(x) ;
    while(! isroot(x)) {
      int y = fa[x] , z = fa[y] ;
      if(! isroot(y)) rotate((rs(z) == y) ^ (rs(y) == x) ? x : y) ;
      rotate(x) ;
    }
  }
  inline void access(int x) {for(int tp = 0 ; x ; tp = x , x = fa[tp]) Splay(x) , rs(x) = tp , pushup(x) ;}
  inline void makeroot(int x) { access(x) ; Splay(x) ; rev[x] ^= 1 ; rever(x) ; }
  inline int findroot(int x) {access(x) ; Splay(x) ; rever(x) ;
    while(ls(x)) rever(x = ls(x)) ;
    return x ;
  }
  inline void split(int x , int y) { makeroot(x) ; access(y) ; Splay(y) ; }
  inline bool chk(int x , int y) { makeroot(x) ; return findroot(y) != x ; }
  inline void link(int x , int y) { makeroot(x) ; fa[x] = y ; }
} lct ;
int st[M << 2] ;
int book[N << 1] ;
signed main() {
  n = read() ; m = read() ;
  for(register int i = 1 ; i <= m ; i ++) { int u = read() , v = read() , w = read() ;
    e[i] = {u , v , w} ;
  } sort(e + 1 , e + m + 1 , cmp) ;
  int idx = n , idnum = 0 ;
  int ll = 1 ; int ans = INT_MAX ;
  for(register int i = 1 ; i <= m ; i ++) {
    ++ idx ;
    int x , y ;
    x = e[i].u , y = e[i].v ;
    if(x == y) { flg[i] = 1 ; continue ; }
    if(lct.chk(x , y)) lct.link(x , idx) , lct.link(idx , y) , idnum ++ ;
    else {
      lct.split(x , y) ;
      int now = lct.id[y] ;
      flg[now - n] = 1 ; lct.Splay(now) ;
      lct.fa[lct.ls(now)] = lct.fa[lct.rs(now)] = 0 ;
      lct.link(x , idx) , lct.link(idx , y) ;
    } while(flg[ll] && ll <= i) ++ ll ;
    if(idnum >= n - 1) ans = min(ans , e[i].w - e[ll].w) ;
  } printf("%lld\n" , ans) ;
	return 0 ;
}

还有两题

• CF1137F Matches Are Not a Child's Play
• CF1172E Nauuo and ODT
  
  先咕着 到时候补…