GHM论文笔记（CVPR2019）

作者要解决的问题
Focal loss(CVPR2017)
- Focal loss的解决方案
- Focal loss的不足
设计思路
最终结果

作者要解决的问题

仍然是one-stage中的一个经典问题，正负、难易样本不均衡。因为anchor的原因，pos : neg>= 1 : 70。负样本大多比较简单，所以也导致了难易样本的问题。

Focal loss(CVPR2017)

Focal loss的解决方案

传统的交叉熵损失函数：
\[
L_{CE} = -[p^*(log(p) + (1-p^*)log(1-p)]
\]
\(p^*=\{0, 1\}\)为真实标签，\(p \in (0, 1)\)为网络的预测概率。可以看到，传统的交叉熵损失函数平等的看待正负样本。
Focal loss
\[
L = -[\alpha p^\gamma p^*log(p) + (1-\alpha)(1-p)^\gamma (1-p^*)log(1-p)]
\]
可以看到Focal loss引入了两个超参数\(\alpha, \gamma\)，\(\alpha\)用来平衡正负样本，\(\gamma\)用来平衡难易样本。简单分析一下，加号的左侧是正样本的损失，右侧是负样本的损失。通过乘上不同的系数\((\alpha, 1-\alpha)\)，来平衡正负样本。对于简单样本，其loss较小，概率值更接近真实标签，这样概率的\(\gamma\)次方越小，相反地，难样本的就会变大，使难样本的损失上升，使网络关注难样本。

Focal loss的不足

虽然Focal loss这篇论文也在一定程度上解决了正负样本不均衡的问题，但是Focal loss引入了两个超参数，调参费劲，且只能应用到box分类上，无法解决回归的问题。

设计思路

梯度与样本的关系

作者观察到难易样本的分布与梯度有着如下的关系，可以看到，梯度较小时（简单样本），样本数量非常多，梯度适中时，样本较少。另外值得注意的一点是，梯度在1左右的样本数量还是不少的。作者将这些样本视为异常值，解决特别难的样本会导致其他的样本准确率下降。

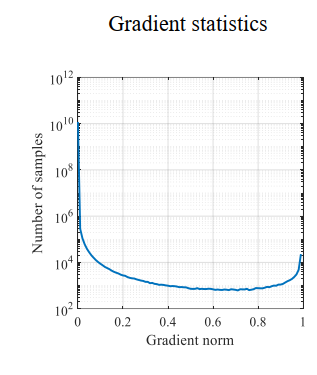
针对以上发现，作者采用梯度分布（梯度附近的样本数）来处理难易样本不平衡的问题。简单思路就是梯度小的样本数比较大，那就给他们乘上一个小系数，梯度大的样本少乘以一个大的系数。不过这个系数不是靠自己调的，而是根据样本的梯度分布来确定的。

梯度分布计算方法：将0-1的梯度切bin，计算每个bin内落入的样本数量。

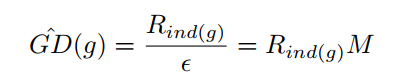
其中\(\epsilon\)是每个bin的宽度，\(M\)是\(\epsilon\)的倒数，表示将0-1切分成多少个bin，\(R_{ind(g)}\)表示每个bin内落入的样本数，计算方法如下：

\[
R_{ind(g)} = \sum_{k=1}^{N} \delta(g_k,g) \quad \delta(g_k,g) =
\begin{cases}
1 \quad if \quad g-\frac{\epsilon}{2} <= g_k <= g+\frac{\epsilon}{2}\\
0 \quad otherwise
\end{cases}
\]

\[
\beta_i = \frac{N}{GD(g_i)}
\]
\(g\)是某点的梯度模，可以理解为以这一点创建一个bin，\(g_k\)是样本的梯度模，N是样本总数。
从上面式子可以看到，梯度分布越大，系数越小。

梯度模计算方法

具体的在二分类中,损失函数为上面提到的交叉熵函数
\[
L_{CE} = -[p^*(log(p) + (1-p^*)log(1-p)] \\
p=sigmoid(x)
\]
对x的梯度
\[
\begin{aligned}\frac{\partial L_{CE}}{\partial x} &= \frac{\partial L_{CE}}{\partial p} \times \frac{\partial p}{\partial x}\\&= (-\frac{p^*}{p} + \frac{1-p^*}{1-p}) \times p(1-p)\\&= p-p^*\end{aligned}
\]
定义梯度模\(g = |p-p^*|\)

改进

GHM－C损失函数

由此，作者提出分类的损失函数GHM-C
\[
L_{GHM-C} = \frac{1}{N}\sum\beta_i L_{CE}(p_i, p_{i}^{*})
\]

还是以这个图为例，在梯度较小时，样本数较大，梯度分布\(GD(g)\)较大，则系数较小，损失较小，这样就有效的减少了大量简单样本的作用。反之亦然。同样可以分析出特别难的样本也被抑制了。这一点也是作者希望看到的。
下面这张图的横坐标代表原先的梯度分布，纵坐标代表处理后的梯度分布。对比未经任何处理的CE曲线，在0附近的梯度，GHM-C处理后梯度被减小了，0.5左右的样本梯度被放大了，尤其值得一提的是，对于前面提到的异常样本，梯度同样被抑制了。对比Focal loss曲线，明显可以看出GHM-C更加优秀。

GHM－R损失函数

按理说像之前一样求下梯度分布就好了，不过这里有一个问题。
对于边框回归的传统损失函数smooth_L1

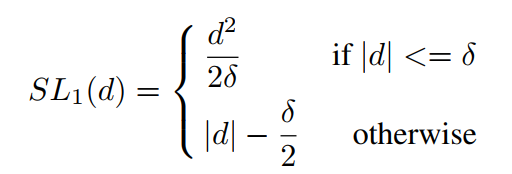
求梯度模
\(d= t_i - t_i^*\)

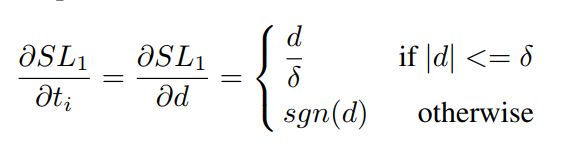
可以看到，当\(d>\delta\)时，梯度模横为1，无法衡量样本的难易程度。所以作者这里改了一下

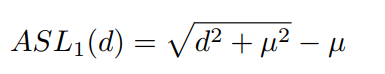
d比较小的时候，类似于\(L_2\)，d较大时候类似\(L_2\)，和\(SL_1\)类似。最终的损失函数如下：

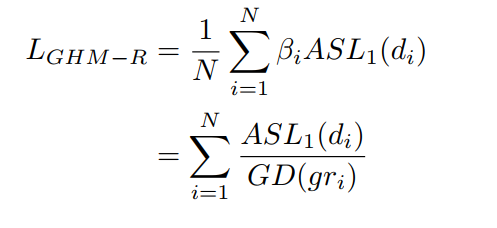
注意一点：回归的损失函数是只计算正样本的。

最终结果

COCO数据集上的比较

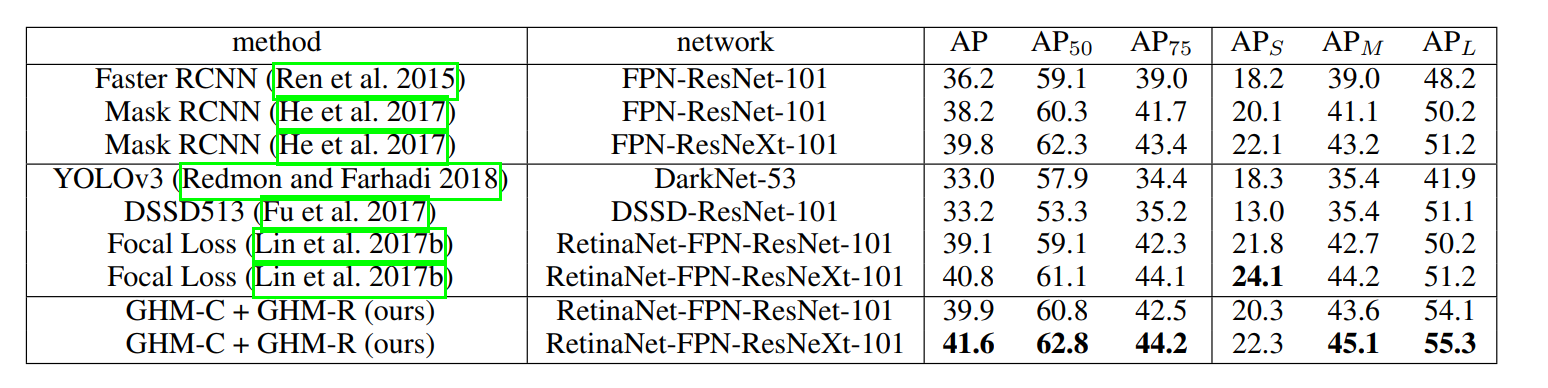
只有GHM-C的比较

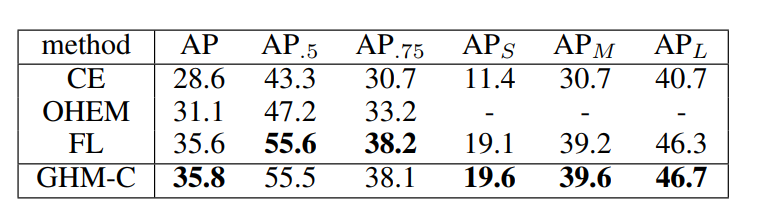
只有GHM-R的比较