This article is made by Jason-Cow.
Welcome to reprint.
But please post the article's address.

莫比乌斯定理（未完待续......）：

形式1：

$F(n)=\sum_{d|n}f(d) =>f(n)=\sum_{d|n}\mu (d)F(\frac{n}{d})$

形式2：

$F(n)=\sum_{n|d}f(d)=>f(n)=\sum_{n|d}\mu(\frac{d}{n})F(d)$

引理:

$\mu(x)=\left\{\begin{matrix} & & 1 (x=1) \\ & & 0(x\neq1 ) \end{matrix}\right.$

证明1：

右边= $f(n)=\sum_{d|n}\mu(d)F(\frac{n}{d})$ 带入左边等式，得

　　　 $=\sum_{d|n} \mu(d) \sum_{k|\frac{n}{d}} f(k)$

　　　　　　 $=\sum_{d|n}\sum_{k|\frac{n}{d}}\mu(d)f(k)$

　　　　　　 $=\sum_{k|n}\sum_{d|\frac{n}{k}}f(k)\mu(d)$

　　　　　　 $=\sum_{k|n}f(k)\sum_{d|\frac{n}{k}}\mu(d)$ 又 $\because$ $\mu(d)\neq 0$ 当且仅当 : $\frac{n}{k}=1$ ，即 $n=k$ 时，上式非 $0$

　　　　　 $=f(n)$

所以， $F(n)=\sum_{d|n}f(d) =>f(n)=\sum_{d|n}\mu (d)F(\frac{n}{d})$ 成立。

bzoj2154

$\sum_{i=1}^{n}\sum_{j=1}^{m}\frac{i*j}{\gcd(i,j)}$

$\sum_{i=1}^{n}\sum_{j=1}^{m}\sum_{g=1}^{n}\frac{i*j}{g}[\gcd(i,j)==g]$

$\sum_{g=1}^{n}\sum_{i=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{g} \right \rfloor}\frac{(i*g)(j*g)}{g}[\gcd(i,j)==1]$

$\sum_{g=1}^{n}\sum_{i=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{g} \right \rfloor}i*j*g*[\gcd(i,j)==1]$

$\sum_{g=1}^{n}g\sum_{i=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{g} \right \rfloor}i*j*[\gcd(i,j)==1]$

$\sum_{g=1}^{n}g\sum_{i=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{g} \right \rfloor}i*j*\sum_{d|\gcd(i,j)}\mu(d)$

$\sum_{g=1}^{n}g\sum_{i=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{g} \right \rfloor}i*j*\sum_{d|i,d|j}\mu(d)$

$\sum_{g=1}^{n}g\sum_{d=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\sum_{i=1}^{\left \lfloor \frac{n}{gd} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{gd} \right \rfloor}(i*d)*(j*d)*\mu(d)$

$\sum_{g=1}^{n}g\sum_{d=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\mu(d)d^{2}\sum_{i=1}^{\left \lfloor \frac{n}{gd} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{gd} \right \rfloor}i*j$

$\sum_{g=1}^{n}g\sum_{d=1}^{\left \lfloor \frac{n}{g} \right \rfloor}\mu(d)d^{2}\sum_{i=1}^{\left \lfloor \frac{n}{gd} \right \rfloor}i\sum_{j=1}^{\left \lfloor \frac{m}{gd} \right \rfloor}j$

时间复杂度

$O(n \sum_{i=1}^{n}\frac{1}{i})=O(n(\ln(n)+C))/*C=0.57721566490153286060651209*/$

换元：令

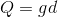
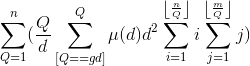
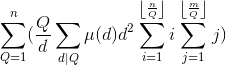
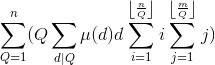
此题的精髓就一个字，模

 #include <algorithm>

 #include <iostream>

 #include <cstring>

 #include <cstdlib>

 #include <cstdio>

 #include <vector>

 #include <cmath>

 #include <queue>

 #include <map>

 #include <set>

 using namespace std;

 #define file(x) freopen(x".in","r",stdin),freopen(x".out","w",stdout)

 const int mod=,maxn=1e7+;

 int f[maxn],p[maxn],flag[maxn],cnt,S[maxn];

 void init(int n,int m){

   f[]=;

   for(int i=;i<=n;i++) {

     if(!flag[i])p[++cnt]=i,f[i]=(-i)%mod;

     for(int j=;j<=cnt && i*p[j]<=n;j++) {

       flag[i*p[j]]=;

       if(i%p[j]==){f[i*p[j]]=f[i]%mod;break;}

       f[i*p[j]]=((long long)(f[i]%mod)*(f[p[j]]%mod))%mod;

     }

   }

   for(int i=;i<=m;i++)S[i]=((S[i]%mod)+((S[i-]+i)%mod))%mod;

 }

 int main(){

   int n,m;scanf("%d%d",&n,&m);if(n>m)swap(n,m);

   init(n,m);

   int ans=;

   for(int Q=;Q<=n;Q++)

     ans=(ans+(((Q%mod)*(long long)f[Q]*(((long long)S[n/Q]*S[m/Q])%mod))%mod)%mod)%mod;

   printf("%d\n",(ans+mod)%mod);

   return ;

 }

Mobius反演定理-BZOJ2154的更多相关文章

Bzoj-2301 [HAOI2011]Problem b 容斥原理,Mobius反演,分块
题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id=2301 题意:多次询问,求有多少对数满足 gcd(x,y)=k, a<=x<=b ...
Mobius反演学习
这篇文章参考了许多资料和自己的理解. 先放理论基础. 最大公约数:小学学过,这里只提一些重要的公式: $·$若$a=b$,则$\gcd(a,b)=a=b$: $·$若$\gcd(a,b)=d$,则$\ ...
YY的GCD
YY的GCD 给出T个询问,询问$\sum_{i=1}^N\sum_{j=1}^M(gcd(i,j)\in prime)$,T = 10000,N, M <= 10000000. 解显然质 ...
Crash的数字表格
Crash的数字表格求$\sum_{i=1}^N\sum_{j=1}^Mlcm(i,j)$ 解设$N<M$,显然有 \[\sum_{i=1}^N\sum_{j=1}^M\frac{i ...
Longge's problem
Longge's problem 求$\sum_{i=1}^ngcd(i,n)$,$n< 2^{31}$. 解理解1: 注意式子的实际意义,显然答案只可能在n的约数中,而现在问题变成了 ...
Sky Code
Sky Code 给出n个数,求选出4个数组合,使其gcd为1,,$n<=10000$,每个数$<=10000$. 解理解1:容斥原理注意到Mobius反演式子不好写出,于是我 ...
LJJ爱数数
LJJ爱数数求\(\sum_{i=1}^n\sum_{j=1}^n\sum_{k=1}^n\epsilon(gcd(i,j,k))(\frac{1}{i}+\frac{1}{j}==\frac{1} ...
[bzoj2154]Crash的数字表格(mobius反演)
题意:$\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {lcm(i,j)} } $ 解题关键: $\sum\limits_{i = 1}^n {\sum\l ...
SPOJ-7001 VLATTICE 莫比乌斯反演定理
题目链接:http://www.spoj.com/problems/VLATTICE/ 题意:求gcd(x,y,z)=1,1<=x,y,z<=n,的个数. 开始做的时候枚举gcd(x,y) ...

随机推荐

CCF CSP 201803-2 碰撞的小球
题目链接:http://118.190.20.162/view.page?gpid=T72 问题描述数轴上有一条长度为L(L为偶数)的线段,左端点在原点,右端点在坐标L处.有n个不计体积的小球在线段 ...
微信小程序获取用户昵称、头像
前段时间微信小程序对获取用户昵称和头像方法进行了更新,网上很多的文章都已经不适用了,这里简单总结一下,首先,传统接口wx.getUserInfo的效果会弹出一个给用户的弹窗,需要用户授权,经过测试传统 ...
How to write a paper in a weekend - by Prof. Pete Carr
Key points: don't procrastinate; review the notes and renew the literature search; determine who you ...
How to read a paper efficiently - by prof. Pete carr
DON'T DO THAT: read the article from the beginning to end; it's a waste of time! READ A PAPER IN TWO ...
1、安装gitlab
1.安装Gitlab Gitlab分为社区版和企业版(收费),这里安装的是ce社区版本方式一: Gitlab官方有提供好的rpm包仓库,所以采用yum安装即可. [root@localhost ~] ...
一些常见的HTTP的请求状态码
200:正确的请求返回正确的结果,如果不想细分正确的请求结果都可以直接返回200. 201:表示资源被正确的创建.比如说,我们 POST 用户名.密码正确创建了一个用户就可以返回 201. 202:请 ...
C++-CodeForces-1313A
真的打起比赛来,连个贪心都写不好,呜呜呜. #include <bits/stdc++.h> using namespace std; ],t,ans; void IF(int&a ...
macaron 根目录默认为templates文件夹，所以如果启动目录同目录下有templates目录，要给它指定另一个文件夹
m *macaron.Macaron //随便指向一个目录,因为web没用到模板,不能使用默认值templates,因为这个目录被其他模板占用了m.Use(macaron.Renderer(macar ...
go语言 base64编码解码
package main import ( "encoding/base64" "fmt" ) func main() { str := "Man&q ...
bootstrap4的改进

Mobius反演定理-BZOJ2154