【二叉搜索树】的详细实现(C++)

二叉搜索树的概念

　　从前面讨论折半搜索的性能中可知，如果每次从搜索序列的中间进行搜索，把区间缩小一半，通过有限次迭代，很快就能通近到所要寻找的元素。进一步，如果我们直接输入搜索序列，构造出类似于折半搜索的判定树那样的树形结构，就能实现快速搜索。这种树形结构就是二又搜索树。

二又搜索树（binary search tree）或者是一棵空树，或者是具有下列性质的二又树：

　　（1）每个结点都有一个作为搜索依据的关键码（key），所有结点的关键码互不相同。

　　（2）左子树（如果存在）上所有结点的关键码都小于根结点的关键码。

　　（3）右子树（如果存在）上所有结点的关键码都大于根结点的关键码。

　　（4）左子树和右子树也是二又搜索树。

　　关键码事实上是结点所保存元素中的某个域的值，它能够唯一地表示这个结点。因此，如果对一棵二又搜索树进行中序遍历，可以按从小到大的顺序，将各结点关键码排列起来，所以也称二叉搜索树为二又排序树（binary sorting tree）。

二叉搜索树的建立

　　输入一系列数据，建立一棵二又搜索树。它要求从空树开始建树，输入序列以输入一个结束标志value结束。这个值应当取不可能在输入序列中出现的值，例如输入序列的值都是正整数时，取RefValue为0或负数。

     //构造BST
     BST(T value) :root(NULL), RefValue(value)
     {
         T x;
         cin >> x;
         while (x != RefValue)
         {
             Insert(x, root);    //新建一个结点，调用Insert插入到树中
             cin >> x;
         }
     }

二叉搜索树的插入

　　为了向二又搜索树中插入一个新元素，必须先检查这个元素是否在树中已经存在。所以在插入之前，先使用搜索算法在树中检查要插入元素有还是没有。如果搜索成功，说明树中已经有这个元素，不再插入；如果搜索不成功，说明树中原来没有关键码等于给定值的结点，把新元素加到搜索操作停止的地方。当ptr!=NULL时，它一定指向一棵子树的根，可用它所包含的关键码与给定值比较继续搜索插入位置；如果 ptr=NULL，一定是递归到空树的位置，此时将创建的新结点地址送给ptr，因为ptr是引用，新结点的地址自然送入上述某一个指针域，自动将新结点作为叶结点链入二又搜索树中了。每次结点的插入，都要从根结点出发搜索插入位置，然后把新结点作为时结点插入。这样不需移动结点，只需修改某个已有树中结点的一个空指针即可。

     //以ptr为根的二叉搜索树中插入所含值为e1的结点
     bool Insert(const T& e1, BSTNode<T>* &ptr)    //第二个参数是指针的引用
     {
         if (ptr == NULL)
         {
             ptr = new BSTNode<T>(e1);    //构造新结点
             if (ptr == NULL)
             {
                 cout << "Memory allocation failed!" << endl;
                 exit();
             }
             return true;
         }
         else if (e1 < ptr->data)    //小于，插入左子树
         {
             Insert(e1, ptr->left);
         }
         else if (e1 > ptr->data)    //大于，插入右子树
         {
             Insert(e1, ptr->right);
         }
         else    //x已在树中，不插入
         {
             return false;
         }
     }

二叉搜索树的递归搜索

　　从根结点开始，沿某一个分支逐层向下进行比较判等的过程。它可以是一个递归的过程。假设想要在二又搜索树中搜索关键码为x的元素，搜索过程从根结点开始。如果根指针为NULL，则搜索不成功；否则用给定值x与根结点的关键码进行比较：如果给定值等于根结点的关键码，则搜索成功，返回搜索成功信息，并报告搜索到的结点地址。如果给定值小于根结点的关键码，则继续递归搜索根结点的左子树，否则，递归搜索根结点的右子树。

     //在ptr为根的二叉搜索树中搜索含x的结点。若找到，返回该结点地址，否则返回NULL
     BSTNode<T>* Search(T x, BSTNode<T>* ptr)
     {
         if (ptr == NULL)
         {
             return NULL;
         }
         else if (x < ptr->data)
         {
             return Search(x, ptr->left);
         }
         else if (x > ptr->data)
         {
             return Search(x, ptr->right);
         }
         else
         {
             return ptr;
         }
     }

二叉搜索树的删除

　　在二又搜索树中删除一个结点时，必须将因删除结点而断开的二又链表重新链接起来，同时确保二叉搜索树的性质不会失去。此外，为了保证在执行删除后，树的搜索性能不至于降低，还需要防止重新链接后树的高度不能增加。

　　如果想要删除叶结点，只需将其父结点指向它的指针清零，再释放它即可。

　　如果被删结点右子树为空，可以拿它的左子女结点顶替它的位置，再释放它。

　　如果被删结点左子树为空，可以拿它的右子女结点顶替它的位置，再释放它。

　　如果被删结点左、右子树都不空，可以在它的右子树中寻找中序下的第一个结点（关键码最小），用它的值填补到被删结点中，再来处理这个结点的删除问题，这是一个递归处理。例如，在上图中想要删除关键码为78的结点，它的左、右子树都不空。在它的右子树中找中序下的第一个结点，其关键码为81。把它的值填补到被删结点中去，下面的问题就是删除关键码为81的结点了。这个结点左子树为空，用它的右子女（关键码为88）代替它的位置就可以了。

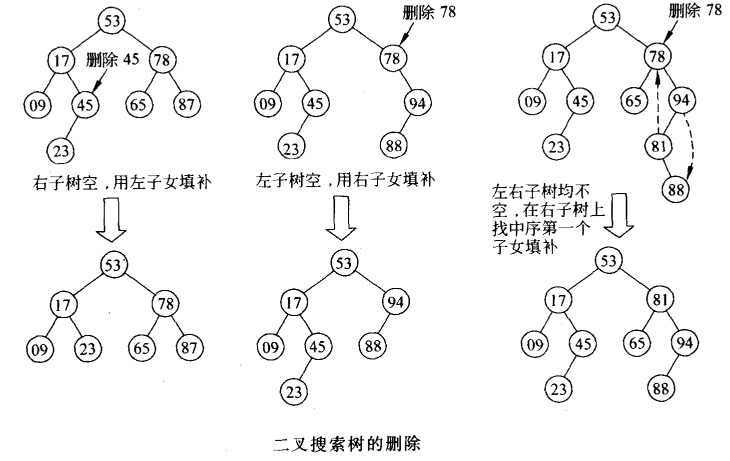
     //以ptr为根的二叉搜索树中删除含x的结点
     bool Remove(T x, BSTNode<T>* &ptr)
     {
         BSTNode<T>* temp;
         if (ptr != NULL) //ptr不为空进行操作
         {
             if (x < ptr->data)
             {
                 Remove(x, ptr->left);
             }
             else if (x > ptr->data)
             {
                 Remove(x, ptr->right);
             }
             //找到了要删除的结点
             //1.要删除的结点ptr同时有左右子树
             else if (ptr->left != NULL&&ptr->right != NULL)
             {
                 temp = ptr->right;    //在右子树中搜索中序下的第一个结点
                 while (temp->left != NULL)
                 {
                     temp = temp->left;
                 }
                 //用右子树中序下的第一个结点的值填充要删除的结点
                 ptr->data = temp->data;
                 //然后再新填充值ptr的右子树中删除temp的data值
                 Remove(ptr->data, ptr->right);
             }
             else //不同时有左右子树
             {
                 temp = ptr;        //temp记住要删除的ptr结点
                 if (ptr->left == NULL) //只有右子树
                 {
                     ptr = ptr->right;
                 }
                 else    //只有左子树
                 {
                     ptr = ptr->left;
                 }
                 delete temp;    //删除结点
                 temp = NULL;
                 return true;
             }
         }
         else //ptr为空直接返回false
         {
             return false;
         }
     }

二叉搜索树的销毁

　　二叉搜索树的销毁与普通二叉树基本相同。

     //销毁以root为根的二叉树搜索树函数
     void Destroy(BSTNode<T>* &root)
     {
         if (root == NULL)
         {
             return;
         }
         if (root->left != NULL)
         {
             Destroy(root->left);
         }
         if (root->right != NULL)
         {
             Destroy(root->right);
         }
         delete root;
         root = NULL;
     }

二叉搜索树的源码

 //二叉搜索树结点类型
 template<typename T>
 struct BSTNode
 {
     T data;    //数据域
     BSTNode<T> *left, *right;    //左子女、右子女
     BSTNode() :left(NULL), right(NULL) {}    //构造函数
     //构造函数
     BSTNode(const T d, BSTNode<T>* L = NULL, BSTNode<T>* R = NULL) :data(d), left(L), right(R) {}
 };

 //二叉搜索树的定义
 template <class T>
 class BST
 {
 public:
     //普通构造函数
     BST() :root(NULL) {}
     //构造BST
     BST(T value) :root(NULL), RefValue(value)
     {
         T x;
         cin >> x;
         while (x != RefValue)
         {
             Insert(x, root);    //新建一个结点，调用Insert插入到树中
             cin >> x;
         }
     }
     //析构
     ~BST() { Destroy(root); }

     //插入
     bool Insert(T x) { return Insert(x, root); }

     //删除
     bool Remove(T x) { return Remove(x, root); }

     //搜索
     bool Search(T x) { return (Search(x, root) != NULL) ? true : false; }

     //中序遍历
     void InOrder() { InOrder(root); }

 protected:

     //以ptr为根的二叉搜索树中插入所含值为e1的结点
     bool Insert(const T& e1, BSTNode<T>* &ptr)    //第二个参数是指针的引用
     {
         if (ptr == NULL)
         {
             ptr = new BSTNode<T>(e1);    //构造新结点
             if (ptr == NULL)
             {
                 cout << "Memory allocation failed!" << endl;
                 exit();
             }
             return true;
         }
         else if (e1 < ptr->data)    //小于，插入左子树
         {
             Insert(e1, ptr->left);
         }
         else if (e1 > ptr->data)    //大于，插入右子树
         {
             Insert(e1, ptr->right);
         }
         else    //x已在树中，不插入
         {
             return false;
         }
     }

     //以ptr为根的二叉搜索树中删除含x的结点
     bool Remove(T x, BSTNode<T>* &ptr)
     {
         BSTNode<T>* temp;
         if (ptr != NULL) //ptr不为空进行操作
         {
             if (x < ptr->data)
             {
                 Remove(x, ptr->left);
             }
             else if (x > ptr->data)
             {
                 Remove(x, ptr->right);
             }
             //找到了要删除的结点
             //1.要删除的结点ptr同时有左右子树
             else if (ptr->left != NULL&&ptr->right != NULL)
             {
                 temp = ptr->right;    //在右子树中搜索中序下的第一个结点
                 while (temp->left != NULL)
                 {
                     temp = temp->left;
                 }
                 //用右子树中序下的第一个结点的值填充要删除的结点
                 ptr->data = temp->data;
                 //然后再新填充值ptr的右子树中删除temp的data值
                 Remove(ptr->data, ptr->right);
             }
             else //不同时有左右子树
             {
                 temp = ptr;        //temp记住要删除的ptr结点
                 if (ptr->left == NULL) //只有右子树
                 {
                     ptr = ptr->right;
                 }
                 else    //只有左子树
                 {
                     ptr = ptr->left;
                 }
                 delete temp;    //删除结点
                 temp = NULL;
                 return true;
             }
         }
         else //ptr为空直接返回false
         {
             return false;
         }
     }

     //在ptr为根的二叉搜索树中搜索含x的结点。若找到，返回该结点地址，否则返回NULL
     BSTNode<T>* Search(T x, BSTNode<T>* ptr)
     {
         if (ptr == NULL)
         {
             return NULL;
         }
         else if (x < ptr->data)
         {
             return Search(x, ptr->left);
         }
         else if (x > ptr->data)
         {
             return Search(x, ptr->right);
         }
         else
         {
             return ptr;
         }
     }

     //中序遍历
     void InOrder(BSTNode<T>* root)
     {
         if (root != NULL)
         {
             InOrder(root->left);
             cout << root->data << " ";
             InOrder(root->right);
         }
     }

     //销毁以root为根的二叉树搜索树函数
     void Destroy(BSTNode<T>* &root)
     {
         if (root == NULL)
         {
             return;
         }
         if (root->left != NULL)
         {
             Destroy(root->left);
         }
         if (root->right != NULL)
         {
             Destroy(root->right);
         }
         delete root;
         root = NULL;
     }
 private:
     BSTNode<T>* root;    //根指针
     T RefValue;    //输入结束标识
 };

 int main(int argc, char* argv[])
 {
     //g a e d f h j i l k #
     BST<char> tree('#');
     tree.InOrder();
     cout << endl;
     cout << tree.Search('e') << endl;
     cout << tree.Insert('z') << endl;
     tree.InOrder();
     cout << endl;
     cout << tree.Remove('z') << endl;
     cout << tree.Remove('j') << endl;
     tree.InOrder();
     cout << endl;
     return ;
 }

源代码