BZOJ3907 网格 卡特兰数

题目描述

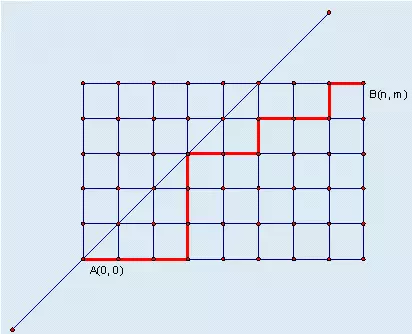
某城市的街道呈网格状，左下角坐标为A(0, 0)，右上角坐标为B(n, m)，其中n >= m。

现在从A(0, 0)点出发，只能沿着街道向正右方或者正上方行走，且不能经过图示中直线左上方的点，即任何途径的点(x, y)都要满足x >= y，

请问在这些前提下，到达B(n, m)有多少种走法。

输入格式

仅有一行，包含两个整数 n 和 m，表示城市街区的规模。

输出格式

仅有一个整数和一个换行/回车符，表示不同的方案总数。

样例

样例输入

6 6

样例输出

132

数据范围与提示

对于全部数据，1≤m≤n≤5000。

卡特兰数折线表示：

n=m：

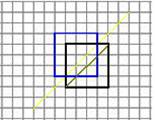
n>m:

博主很懒连打字都不想打了

好吧其实n=m时你会发现是卡特兰数，当n>m时，我们把黑色沿绿线翻折，得到另一块黑色，

如果我们只用卡特兰数，会算上紫框里的部分（由a到c），所以减去

n=m也是一样，只是式子化简一下就是卡特兰数

用到高精，高精你会TLE，所以要把式子化简一下

没啥可说的，普及一下CATALAN数

卡特兰数是组合数学中经常出现在计数问题的数列，

满足：h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)

另一种递推公式：h(n)=$\frac{(n-1)*(4*n-2)}{n+1}$

通项公式：h(n)=$C_{2*n}^{n}-C_{2*n}^{n-1}$

　　　　　h(n)=$\frac{C_{2*n}^{n}}{n+1}$

应用：

出栈次序是卡特兰数的一个应用。

我们将入栈视为+1，出栈视为-1，则限制条件为在任意位置前缀和不小于0 。

我们讨论这个问题与卡特兰数有什么关系。

为了方便，我们按入栈的先后顺序将各个元素由1到n编号。

假设最后一个出栈的数为k。 则在k入栈之前，比k小的数一定全部出栈，所以这部分方案数为h(k-1)。

在k入栈之后，比k大的数在k入栈之后入栈，

在k出栈之前出栈，所以这部分的方案数为h(n-k)。

这两部分互不干扰，则方案数为h(k-1)*h(n-k) 枚举k，得到的公式就是卡特兰数的递推公式。

卡特兰数的应用

　　括号匹配

　　二叉树计数

　　有限制的网格路径数

好了先普及这些，放代码：

#include<bits/stdc++.h>
#define re register
#define MAXN 50005
using namespace std;
int n,m;
struct node{
	int m[MAXN];
	node(){memset(m,0,sizeof(m));}
	inline friend void operator *= (node &a,re int b){
		int x=0;
		for(re int i=1;i<=a.m[0];i++){
			re int y=a.m[i]*b+x;
			a.m[i]=y%10;
			x=y/10;
		}
		while(x){
		    a.m[++a.m[0]]=x%10;
		    x/=10;
		}
	}
	inline friend void operator /= (node &a,re int b){
		re int x=0;
		for(re int i=a.m[0];i>=1;i--){
			x+=a.m[i];
			a.m[i]=x/b;
			x%=b;
			x*=10;
		}
		while(a.m[a.m[0]]==0&&a.m[0]>1)
			a.m[0]--;
	}
	inline friend node operator - (node a,node b){
		node c;
		re int i=1;
		while((i<=a.m[0])||(i<=b.m[0])){
			if(a.m[i]<b.m[i]){
				a.m[i]+=10;
				a.m[i+1]--;
			}
			c.m[i]=a.m[i]-b.m[i];
			i++;
		}
		while(c.m[i]==0&&i>1)
			i--;
		c.m[0]=i;
		return c;
	}
	inline friend void print(node a){
		for(re int i=a.m[0];i>=1;i--)
			printf("%d",a.m[i]);
		puts("");
	}
}x;
int main(){
	scanf("%d%d",&n,&m);
	x.m[0]=x.m[1]=1;
	for(re int i=m+1;i<=n+m;i++) x*=i;
	x*=(n-m+1);
	for(re int i=2;i<=n+1;i++) x/=i;
	print(x);
	return 0;
}