【算法】实现字典API:有序数组和无序链表
- 有序数组
- 无序链表
(二叉树的实现方案将在下一篇文章介绍)
字典的定义和相关操作
- 查询某个特定的数据是否在查找表中
- 检索某个特定的数据元素的各种属性
- 在查找表中插入一个数据元素
- 从查找表中删除某个数据元素
有序数组实现字典
有序数组实现字典思路



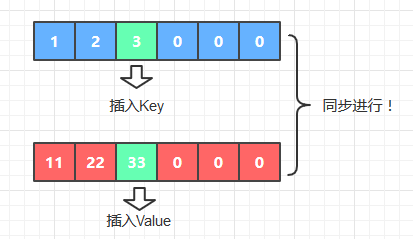
Key和Value的位置是相同的
字典长度和数组长度
- 数组长度是创建后固定不变的,例如一开始就是N
- 字典的长度是可变的, 开始是0, 逐渐递增到N。


选择有序数组的原因
- 选择无序数组实现字典, 也就意味着选择了顺序查找。
- 而选择有序数组实现字典, 代表着你可以选择二分查找(或插值查找等), 并享受查找性能上的巨大提升。
三个成员变量,一个核心方法
public class BinarySearchST {
int [] keys; // 存储key
int [] vals; // 存储value
int N = 0; // 计算字典长度
public BinarySearchST (int n) { // 根据输入的数组长度初始化keys和vals
keys = new int[n];
vals = new int[n];
}
public int rank (int key) { // 查找Key的位置并返回
// 核心方法
}
public void put (int key, int val) {
// 通过一些方式调用rank
}
public int get (int key) {
// 通过一些方式调用rank
}
public int delete (int key) {
// 通过一些方式调用rank
}
}
无序链表实现的字典API
1. rank方法
- 查找成功,返回Key的位置
- 查找失败(Key不存在),返回 - 1
- 查找成功,返回Key的位置
- 查找失败(Key不存在),返回小于给定Key的元素数量
public int rank (int key) {
int mid;
int low= 0,high = N-1;
while (low<=high) {
mid = (low + high)/2;
if(key<keys[mid]) {
high = mid - 1;
}
else if(key>keys[mid]) {
low = mid + 1;
}
else {
return mid; // 查找成功,返回Key的位置
}
}
return low; // 返回小于给定Key的元素数量
}
2. put方法
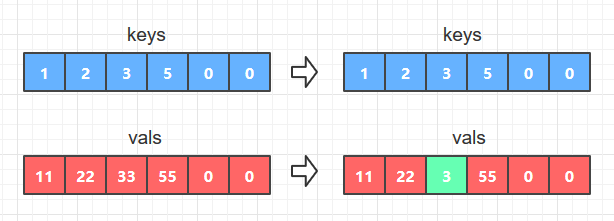
- 如果key等于keys[i],说明查找成功, 那么只要替换vals数组中的vals[i]为新的val就可以了,如图A
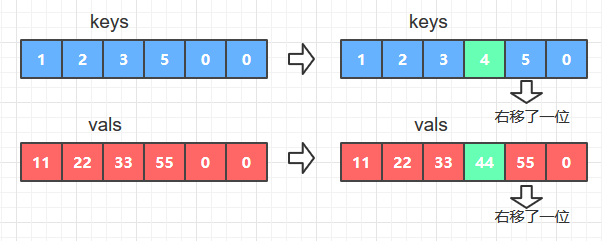
- 如果key不等于keys[i],那么在字典中插入新的 key-val键值对,具体操作是将数组keys和vals中大于给定key和val的元素全部右移一位, 然后使keys[i]=key; vals[i] = val; 如图B


public void put (int key, int val) {
int i = rank(key);
if(i<N&&key == keys[i]) { // 查找到Key, 替换vals[i]为val
vals[i] = val;
return ; // 返回
}
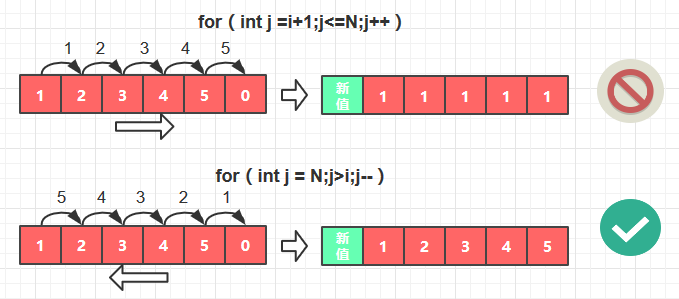
for (int j=N;j>i;j-- ) { // 未查找到Key
keys[j] = keys[j-1]; // 将keys数组中小于key的值全部右移一位
vals[j] = vals[j-1]; // 将vals数组中小于val的值全部右移一位
}
keys[i] = key; // 插入给定的key
vals[i] = val; // 插入给定的val
N++;
}


for (int j=N;j>i;j-- ) {
}
for (int j=i + 1;j<=N;j++ ) {
}

3. get方法
public boolean isEmpty () {
return N == 0;
} // 判断字典是否为空(不是数组!)
public int get (int key) {
if(isEmpty()) return -1; // 当字典为空时,不需要进行查找,提示操作失败
int i = rank(key);
if(i<N&&keys[i] == key) {
return vals[i]; // 当查找成功时候, 返回和key对应的value值
}
return -1; // 没有查找到给定的key,提示操作失败
}
4. delete方法
- 和get方法一样, 查找前要通过isEmpty判断字典是否为空,是则无需删除
- 和put方法类似, 删除要将keys/vals中大于key/value的元素全部“左移一位”
public int delete (int key) {
if(isEmpty()) return -1; // 字典为空, 无需删除
int i = rank(key);
if(i<N&&keys[i] == key) { // 当给定key存在时候,删除该key-value对
for(int j=i;j<=N-1;j++) {
keys[j] = keys[j+1]; // 删除key
vals[j] = keys[j+1]; // 删除value
}
N--; // 字典长度减1
return key; // 删除成功,返回被删除的key
}
return -1; // 未查找到给定key,删除失败
}
for (int j=N;j>i;j-- ) { }
for(int j=i;j<=N-1;j++) { }
5. floor方法

public int floor (int key) {
int k = get(key); // 查找key, 返回其value
int rank = rank(key); // 返回给定key的位置
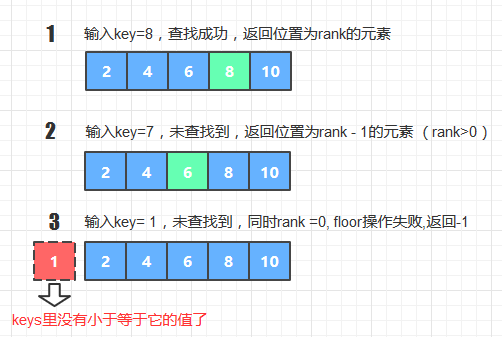
if(k!=-1) return key; // 查找成功,返回值为key
else if(k==-1&&rank>0) return keys[rank-1]; // 未查找到key,同时给定key并没有排在字典最左端,则返回小于key的前一个值
else return -1; // 未查找到key,给定Key排在字典最左端,没有floor值
}
6. ceiling方法
代码
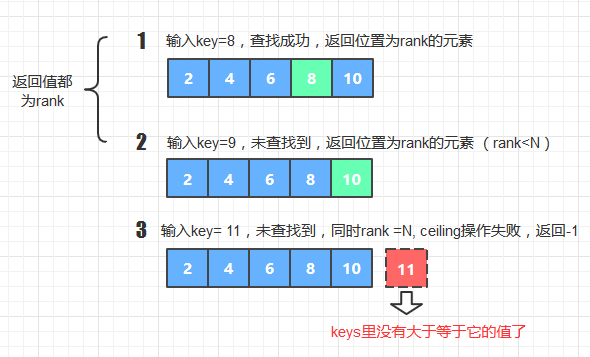
public int ceiling (int key) {
int k = rank(key);
if(k==N) return -1;
return keys[k];
}

7. size方法
public int size () { return N; }
- 在声明N的时候初始化了: int N = 0;
- put操作完成时执行了N++
- delete操作完成时执行了N--;
8. max, min,select方法
public int max () { return keys[N-1]; } // 返回最大的key
public int min () { return keys[0]; } // 返回最小的key
public int select (int k) { // 根据下标返回key
if(k<0||k>N) return -1;
return keys[k];
}
9. resize
keys = tempKeys;
vals = tempVals;
private void resize (int max) { // 调整数组大小
int [] tempKeys = new int[max];
int [] tempVals = new int[max];
for(int i=0;i<N;i++) {
tempKeys[i] = keys[i];
tempVals[i] = vals[i];
}
keys = tempKeys;
vals = tempVals;
}
// 字典长度赶上了数组长度,将数组长度扩大为原来的2倍
if(N == keys.length) { resize(2*keys.length) }
/**
* @Author: HuWan Peng
* @Date Created in 11:54 2017/12/10
*/
public class BinarySearchST {
int [] keys;
int [] vals;
int N = 0;
public BinarySearchST (int n) {
keys = new int[n];
vals = new int[n];
} public int size () { return N; } public int max () { return keys[N-1]; } // 返回最大的key public int min () { return keys[0]; } // 返回最小的key public int select (int k) { // 根据下标返回key
if(k<0||k>N) return -1;
return keys[k];
} public int rank (int key) {
int mid;
int low= 0,high = N-1;
while (low<=high) {
mid = (low + high)/2;
if(key<keys[mid]) {
high = mid - 1;
}
else if(key>keys[mid]) {
low = mid + 1;
}
else {
return mid;
}
}
return low;
} public void put (int key, int val) {
int i = rank(key);
if(i<N&&key == keys[i]) { // 查找到Key, 替换vals[i]为val
vals[i] = val;
return ; // 返回
}
for (int j=N;j>i;j-- ) { // 未查找到Key
keys[j] = keys[j-1]; // 将keys数组中小于key的值全部右移一位
vals[j] = vals[j-1]; // 将vals数组中小于val的值全部右移一位
}
keys[i] = key; // 插入给定的key
vals[i] = val; // 插入给定的val
N++;
} public boolean isEmpty () {
return N == 0;
} // 判断字典是否为空(不是数组!) public int get (int key) {
if(isEmpty()) return -1; // 当字典为空时,不需要进行查找,提示操作失败
int i = rank(key);
if(i<N&&keys[i] == key) {
return vals[i]; // 当查找成功时候, 返回和key对应的value值
}
return -1; // 没有查找到给定的key,提示操作失败
} public int delete (int key) {
if(isEmpty()) return -1; // 字典为空, 无需删除
int i = rank(key);
if(i<N&&keys[i] == key) { // 当给定key存在时候,删除该key-value对
for(int j=i;j<=N-1;j++) {
keys[j] = keys[j+1]; // 删除key
vals[j] = keys[j+1]; // 删除value
}
N--; // 字典长度减1
return key; // 删除成功,返回被删除的key
}
return -1; // 未查找到给定key,删除失败
} public int ceiling (int key) {
int k = rank(key);
if(k==N) return -1;
return keys[k];
} public int floor (int key) {
int k = get(key); // 查找key, 返回其value
int rank = rank(key); // 返回给定key的位置
if(k!=-1) return key; // 查找成功,返回值为key
else if(k==-1&&rank>0) return keys[rank-1]; // 未查找到key,同时给定key并没有排在字典最左端,则返回小于key的前一个值
else return -1; // 未查找到key,给定Key排在字典最左端,没有floor值
} }
无序链表
字典类的结构
public class SequentialSearchST {
Node first; // 头节点
int N = 0; // 链表长度
private class Node { // 内部Node类
int key;
int value;
Node next; // 指向下一个节点
public Node (int key,int value,Node next) {
this.key = key;
this.value = value;
this.next = next;
}
}
public void put (int key, int value) { }
public int get (int key) { }
public void delete (int key) { }
}

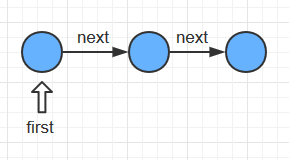
链表和数组在实现字典的不同点
无序链表实现的字典API
1. put 方法
public void put (int key, int value) {
for(Node n=first;n!=null;n=n.next) { // 遍历链表节点
if(n.key == key) { // 查找到给定的key,则更新相应的value
n.value = value;
return;
}
}
// 遍历完所有的节点都没有查找到给定key
// 1. 创建新节点,并和原first节点建立“next”的联系,从而加入链表
// 2. 将first变量修改为新加入的节点
first = new Node(key,value,first);
N++; // 增加字典(链表)的长度
}
first = new Node(key,value,first);
Node newNode = new Node(key,value,first); // 1. 创建新节点,并和原first节点建立“next”的联系
first = newNode // 2. 将first变量修改为新加入的节点


2. get方法
public int get (int key) {
for(Node n=first;n!=null;n=n.next) {
if(n.key==key) return n.value;
}
return -1;
}
3. delete方法
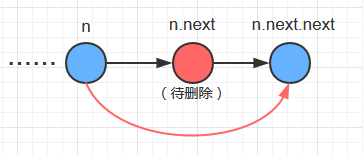
public void delete (int key) {
for(Node n =first;n!=null;n=n.next) {
if(n.next.key==key) {
n.next = n.next.next;
N--;
return ;
}
}
}
if(n.next.key==key) {
n.next = n.next.next;
}

/**
* @Author: HuWan Peng
* @Date Created in 17:26 2017/12/10
*/
public class SequentialSearchST {
Node first; // 头节点
int N = 0; // 链表长度
private class Node {
int key;
int value;
Node next; // 指向下一个节点
public Node (int key,int value,Node next) {
this.key = key;
this.value = value;
this.next = next;
}
}
public int size () {
return N;
}
public void put (int key, int value) {
for(Node n=first;n!=null;n=n.next) { // 遍历链表节点
if(n.key == key) { // 查找到给定的key,则更新相应的value
n.value = value;
return;
}
}
// 遍历完所有的节点都没有查找到给定key
// 1. 创建新节点,并和原first节点建立“next”的联系,从而加入链表
// 2. 将first变量修改为新加入的节点
first = new Node(key,value,first);
N++; // 增加字典(链表)的长度
}
public int get (int key) {
for(Node n=first;n!=null;n=n.next) {
if(n.key==key) return n.value;
}
return -1;
}
public void delete (int key) {
for(Node n =first;n!=null;n=n.next) {
if(n.next.key==key) {
n.next = n.next.next;
N--;
return ;
}
}
}
}
有序数组和无序链表实现字典的性能差异
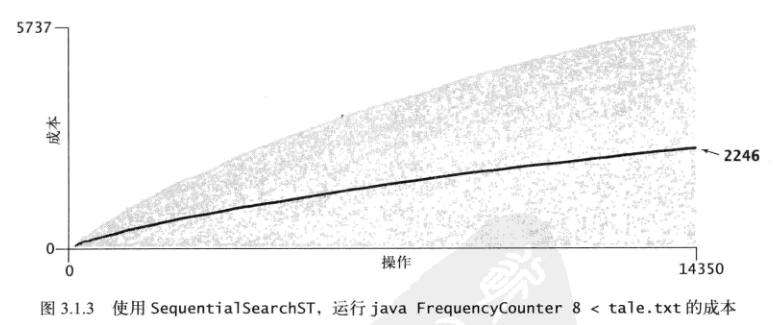



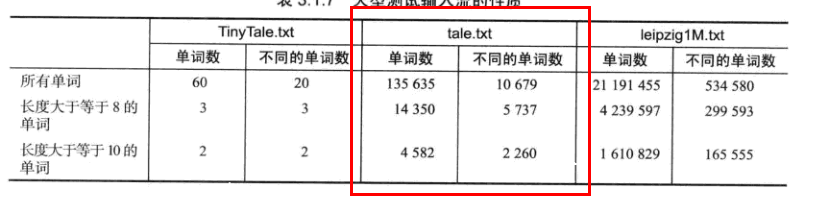


【算法】实现字典API:有序数组和无序链表的更多相关文章
- 【算法】字典的诞生:有序数组 PK 无序链表
参考资料 <算法(java)> — — Robert Sedgewick, Kevin Wayne <数据结构> ...
- 《Java数据结构与算法》笔记-CH2有序数组
/** * 上个例子是无序数组,并且没有考虑重复元素的情况. * 下面来设计一个有序数组,我们设定不允许重复,这样提高查找的速度,但是降低了插入操作的速度. * 1.线性查找 * 2.二分查找 * 有 ...
- java面向对象的有序数组和无序数组的比较
package aa; class Array{ //定义一个有序数组 private long[] a; //定义数组长度 private int nElems; //构造函数初始化 public ...
- Python中将字典转换为有序列表、无序列表的方法
说明:列表不可以转换为字典 1.转换后的列表为无序列表 a = {'a' : 1, 'b': 2, 'c' : 3} #字典中的key转换为列表 key_value = list(a.keys()) ...
- (算法)两个有序数组的第k大的数
题目: 有两个数组A和B,假设A和B已经有序(从大到小),求A和B数组中所有数的第K大. 思路: 1.如果k为2的次幂,且A,B 的大小都大于k,那么 考虑A的前k/2个数和B的前k/2个数, 如果A ...
- 算法-求两个有序数组两两相加的值最小的K个数
我的思路是: 用队列, 从(0,0)開始入队,每次出队的时候,选(1,0) (0,1) 之间最小的入队,假设是相等的都入队,假设入过队的就不入了,把出队的k个不同的输出来就可以 我測试了几组数据都是 ...
- iOS常用算法之两个有序数组合并, 要求时间复杂度为0(n)
思路: 常规思路: 先将一个数组作为合并后的数组, 然后遍历第二个数组的每项元素, 一一对比, 直到找到合适的, 就插入进去; 简单思路: 设置数组C, 对比A和B数组的首项元素, 找到最小的, 就放 ...
- python经典面试算法题1.2:如何从无序链表中移除重复项
本题目摘自<Python程序员面试算法宝典>,我会每天做一道这本书上的题目,并分享出来,统一放在我博客内,收集在一个分类中. 1.2 如何实现链表的逆序 [蚂蚁金服面试题] 难度系数:⭐⭐ ...
- 【算法】二叉查找树实现字典API
参考资料 <算法(java)> — — Robert Sedgewick, Kevin Wayne <数据结构> ...
随机推荐
- IDEA导入Eclipse项目
目录 一.导入项目 二.启动项目 一.导入项目 1.欢迎界面,选择Import Project 2.选择源码的位置,点击OK 3.选择Eclipse模型,点击Next 4.默认选择,点击Next 5. ...
- Swift 通过运行时获取属性名列表
import UIKit //必须要有@objcMembers修饰符,否则获取到的成员属性为0 @objcMembers class Person: NSObject { var name: Stri ...
- ElasicSearch(2) Linux运行
1.org.elasticsearch.bootstrap.StartupException: java.lang.RuntimeException: can not run elasticsearc ...
- 设置 VS 工程目录不保存 sdf / VC.db 文件和 Ipch 文件夹
使用 Visual Studio 建立 C++ 解决方案时,会生成 SolutionName.sdf(Visual Studio 2015 Update 2 后改为 project_name.VC.d ...
- 深入剖析GPU Early Z优化
最近在公司群里同事发了一个UE4关于Mask材质的优化,比如在场景中有大面积的草和树的时候,可以在很大程度上提高效率.这其中的原理就是利用了GPU的特性Early Z,但是它的做法跟我最开始的理解有些 ...
- MySQL中IN子查询会导致无法使用索引
今天看到一个博客园的一篇关于MySQL的IN子查询优化的案例,一开始感觉有点半信半疑(如果是换做在SQL Server中,这种情况是绝对不可能的,后面会做一个简单的测试.)随后动手按照他说的做了一个表 ...
- Linux命令行报错 bash: cannot create temp file for here-document: No space left on device
今天Linux服务器出问题了,使用"tab"补全命令时,提示 bash: cannot create temp file for here-document: No space l ...
- [leetcode]72. Edit Distance 最少编辑步数
Given two words word1 and word2, find the minimum number of operations required to convert word1 to ...
- laravel简书(2)
用户注册 public function register() { //验证 $this->validate(\request(),[ ' ...
- Python开发——函数【装饰器、高阶函数、函数嵌套、闭包】
装饰器 装饰器本质就是函数,为其他函数添加附加功能. 原则: 不修改被修饰函数的源代码 不修改被修饰函数的调用方法 装饰器知识储备:装饰器 = 高阶函数 + 函数嵌套 + 闭包 案例:求函数运行时间! ...
