C#二分查找算法设计实现

C#二分查找算法设计实现

1.介绍

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。(记住了前提要求是顺序存储结构，而且要有序排序，所以说对于一个无序的是没法用二分查找的）

2.查找算法过程

举例就一个int类型数组为例 比如int[] intArray；

假设数组中元素是按升序排列，将数组中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

复杂度：O（lg n），n为要查找的元素个数。

3.算法要求

1. 必须采用顺序存储结构。
2. 必须按关键字大小有序排列。

4.算法实现

这里以C#代码实现

4.1递归方法

         /// <summary>
         /// 二分查找递归实现
         /// </summary>
         /// <param name="arr">数组</param>
         /// <param name="low">开始索引 0</param>
         /// <param name="high">结束索引 </param>
         /// <param name="key">要查找的对象</param>
         /// <returns>返回索引</returns>
         public static int BinarySearch(int[] arr, int low, int high, int key)
         {
             int mid = (low + high) / ;//中间索引
             if (low > high)
                 return -;
             else
             {
                 if (arr[mid] == key)
                     return mid;
                 else if (arr[mid] > key)
                     return BinarySearch(arr, low, mid - , key);
                 else
                     return BinarySearch(arr, mid + , high, key);
             }
         }

4.2While循环实现

         /// <summary>
         /// 二分查找While循环实现
         /// </summary>
         /// <param name="nums">数组</param>
         /// <param name="low">开始索引</param>
         /// <param name="high">结束索引</param>
         /// <param name="target">要查找的对象</param>
         /// <returns>返回索引</returns>
         public static int BinaryWhile(int[] nums, int low, int high, int target)
         {
             while (low <= high)
             {
                 int middle = (low + high) / ;
                 if (target == nums[middle])
                 {
                     return middle;
                 }
                 else if (target > nums[middle])
                 {
                     low = middle + ;
                 }
                 else if (target < nums[middle])
                 {
                     high = middle - ;
                 }
             }
             return -;
         }

5.测试代码

         static void Main(string[] args)
         {
             int[] intArray = new int[] { ,,,,,,,,,};
             int result = BinarySearch(intArray,,intArray.Length-,);
             Console.WriteLine(result.ToString());
             Console.WriteLine("-------------------------------------------");
             int resuleWhile = BinaryWhile(intArray,,intArray.Length-,);
             Console.WriteLine(resuleWhile.ToString());
             Console.Read();
         }

6.输出结果

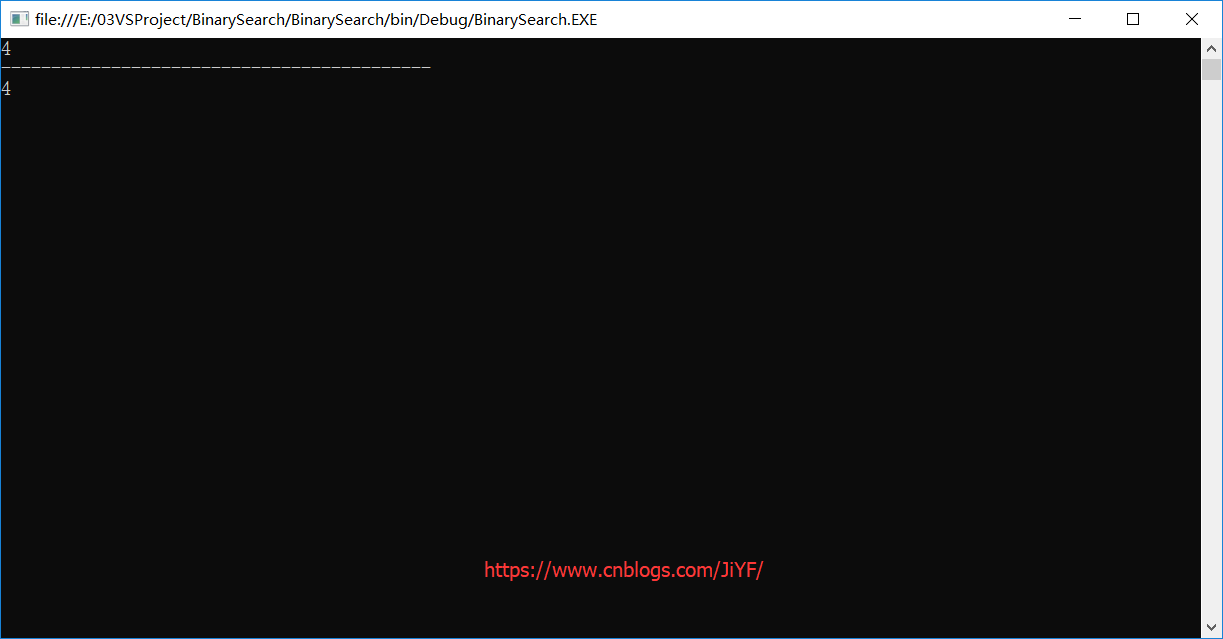
7.源代码工程下载

源码工程项目文件下载