[CF1041F Ray in the tube][数学]
http://codeforces.com/contest/1041/problem/F
题目大意:
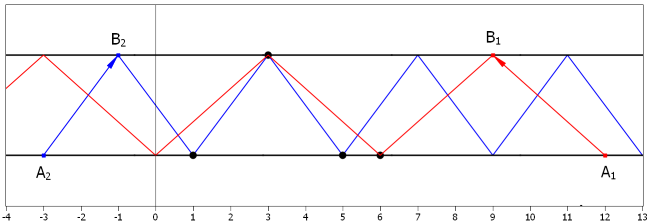
下边界有n个给定点,上边界有m个给定点,可以从任意一个点发出一条激光,激光碰到边界会反射
激光到达边界必须打到整数点,问最多可以打到几个给定点
输入格式:
第一行两个整数n,y1,表示下边界给定点的个数和下边界的纵坐标
第二行n个整数,表示给定点的横坐标
第三行两个整数m,y2,表示上边界给定点的个数和上边界的纵坐标
第四行m个整数,表示给定点的横坐标
题解:设起点横坐标为Xa,步长为Dx,则经过的第一行的点满足X=Xa+2*k*Dx,第二行的点满足X=Xa+(2*k+1)*Dx,发现步长为1时经过的点总可以覆盖步长Dx为奇数的点,所以可以通过步长为1来代替步长为奇数的情况,而当步长Dx为偶数时(即Dx=a*b,a为奇数,b为偶数),总可以转化成步长为b的情况,所以偶数都可以转化成步长为2的整数幂的情况,综上可得,只需要枚举2的0~29次幂即可,使用map存下来所有数%(2*Dx)的数量即可
[CF1041F Ray in the tube][数学]的更多相关文章
- CF1041F Ray in the tube
挂上Chester大神的解题报告 有一个思维跳跃的地方,就是不应该枚举所有的$B$点,而是应该在选定一个$A$点之后枚举距离计算. 然后我们发现枚举距离是$2^k$的长度就可以了,证明如下: 假如距离 ...
- CF1041F Ray in the tube构造_思维
不难发现起点必定是一个点. 每次间隔的距离一定是 2k2^k2k,关键就是要判断两点是否在同一跳跃距离上可被同时覆盖. 我们可以对上边进行 x1≡x_{1}\equivx1≡ x2mod(2∗dx) ...
- L - Ray in the tube Gym - 101911L (暴力)
---恢复内容开始--- You are given a tube which is reflective inside represented as two non-coinciding, but ...
- Codeforces 1041F Ray in the tube (看题解)
Ray in the tube 感觉是套路题.. 如果确定一个差值x我们如何取确定答案呢, 我们把a[ i ] -> a[ i ] % (2 * x), 把b[ i ] -> (b[ i ...
- CF 1041 F. Ray in the tube
F. Ray in the tube 链接 题意: 有两条平行于x轴的直线A,B,每条直线上的某些位置有传感器.你需要确定A,B轴上任意两个整点位置$x_a$,$x_b$,使得一条光线沿$x_a→x_ ...
- Codeforces | CF1041F 【Ray in the tube】
昨天晚上全机房集体开\(Div2\),因为人傻挂两次\(B\)题的我开场就\(rank2000+\dots qwq\)于是慌乱之中的我就开始胡乱看题(口胡),于是看了\(F\dots\)(全机房似乎也 ...
- Codeforces.1041F.Ray in the tube(思路)
题目链接 \(Description\) 有两条平行于\(x\)轴的直线\(A,B\),每条直线上的某些位置有传感器.你需要确定\(A,B\)轴上任意两个整点位置\(x_A,x_B\),使得一条光线沿 ...
- Codeforces Round #509 (Div. 2) F. Ray in the tube(思维)
题目链接:http://codeforces.com/contest/1041/problem/F 题意:给出一根无限长的管子,在二维坐标上表示为y1 <= y <= y2,其中 y1 上 ...
- 【杂题】cf1041fF. Ray in the tube
死于没有处理边界 题目描述 题目大意 在两面镜子上各选定一个整数位置的点 A 与 B,并从其中一个点向另一个射出一条光线,使得接收到光线的传感器数量尽可能的多.传感器不重叠. 题目分析 我们来初步考虑 ...
随机推荐
- Vue提供操作DOM的方法
<div ref="wrapper"> Vue.js 提供了我们一个获取 DOM 对象的接口—— vm.$refs.在这里,我们通过了 this.$refs.wrapp ...
- IOS面试题2018/11/17
1.设计模式是什么?你知道哪些设计模式? 设计模式是一种编码经验,就是一种成熟的逻辑去处理某一种类型的事情. 1.MVC模式:model view controller,把模型,视图,控制器 层进行解 ...
- 09.vue中样式-style
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- loadrunner中web_reg_save_param和web_reg_save_param_ex的区别
在使用Loadrunner进行性能测试,编写接口请求脚本时,通过会用到关联函数,而web_reg_save_param和web_reg_save_param_ex的函数有什么区别呢?以下为总结的两点, ...
- Rancher2.0中使用外置NFS存储部署Nginx实验
目录: 1.环境准备工作 1.1 准备好Rancher2.0集群环境 1.2 准备好外部NFS服务器 2.Rancher2.0中使用NFS存储的方法 2.1 在集群中创建持久卷(PV) 2.2 在项目 ...
- 用GraphX分析伴生网络(一)
1. 图论与GraphX 图论是一个数学学科,研究一组实体(称为顶点)之间两两关系(称为边)的特点.通过构建关系图谱,并对关系进行分析,可以实现更好的投放广告,推荐关系等.随着关系图谱越来越强大,计算 ...
- Archiva 2.2.3 安装运行的时候出现协议版本错误
在 Archiva 安装成功后运行的时候出现协议版本错误: Caused by: javax.net.ssl.SSLException: Received fatal alert: protocol_ ...
- Android 回调函数的理解,实用简单(回调函数其实是为传递数据)
作者: 夏至,欢饮转载,也请保留这段申明 http://blog.csdn.net/u011418943/article/details/60139910 一般我们在不同的应用传递数据,比较方便的是用 ...
- netty-socketio(一)之helloworld,与springboot整合
netty-socketio是一个开源的Socket.io服务器端的一个java的实现, 它基于Netty框架. 1.参考资料 (1)netty-socketio项目github地址: https:/ ...
- 2015-10-05 js3
Javascript 实例2九九乘法表 var s = ""; s += "<table>"; for (var i = 1; i < 10; ...
