MATLAB用二分法、不动点迭代法及Newton迭代（切线）法求非线性方程的根

作者：凯鲁嘎吉 - 博客园
http://www.cnblogs.com/kailugaji/

一、实验原理

二、实验步骤

三、实验过程

1.(程序)

（1）二分法：求在区间（1，2）之间的根，取

（a）bipart.m:

function [x,m]=bipart(fun,a0,b0,tol)

a=a0;b=b0;

m=1+round(round(log((b-a)/tol))/log(2));

for k=1:m

    p=(a+b)/2;

    if fun(p)*fun(b)<0

            a=p;

    else

            b=p;

    end

    x=p;

end

(b)fun1.m:

function f=fun1(x)

f=x^3+10*x-20;

（2）不动点迭代法：求方程在附近的根，取

（a）budong.m:

function [x,k]=budong(fun,x0,tol,m)

for k=1:m

    x=fun(x0);

    if abs(x-x0)<tol

        break;

    end

    x0=x;

end

x=vpa(x,8);

(b)fun.m

function t=fun(x1)

syms x;

f=x^3-2*x-5;

s=subs(diff(f,x),x,x1);

x=x1;

f=x^3-2*x-5;

t=x-f/s;

（3）牛顿迭代法：求方程在附近的根，取

newton.m:

function x1=newton(t1,esp,m)

syms x;

fun=x^3+2*x-5;

for k=1:m

    if abs(subs(diff(fun,'x'),x,t1))<esp

        x1=t1;

        break;

    else

        if subs(diff(fun,'x',2),x,t1)==0

            break;

            disp('解题失败！')

        else

            t0=t1;

            t1=t0-subs(fun,x,t0)/subs(diff(fun,'x'),x,t0);

            if abs(t1-t0)<esp

                x1=t1;

                break;

            end

        end

    end

end

x1=vpa(x1,8);

2.(运算结果)

（1）二分法：

>> [x,m]=bipart(@fun1,1,2,0.0001)

x =

    1.5945

m =

    14

(2)不动点迭代法：

>> [x,k]=budong(@fun,2,1e-5,100)

x =

2.0945515

k =

     4

(3)牛顿迭代法：

 >> x1=newton(2,1e-4,20)

     x1 =

        1.3282689

3.(拓展（方法改进、体会等）)

对于方程的根为重根的情形，newton法求重根只是线性收敛，迭代缓慢，如果对于求重根的情形，对newton法进行改进，取

，

则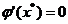。用迭代法

求m重根，则具有二阶收敛性，但要知道的重数m。

计算方程的根是二重根，用newton法与改进方法求根。

源程序：

newton_biroot.m:

function t=newton_biroot(x1)

syms x;

f=x^4-4*(x^2)+4;

s=subs(diff(f,x),x,x1);

x=x1;

f=x^4-4*(x^2)+4;

t=x-f/s;

biroot1.m:

function t=biroot1(x1)

syms x;

f=x^4-4*(x^2)+4;

s=subs(diff(f,x),x,x1);

x=x1;

f=x^4-4*(x^2)+4;

t=x-2*f/s;

budong.m:

function [x,k]=budong(fun,x0,tol,m)

for k=1:m

    x=fun(x0);

    if abs(x-x0)<tol

        break;

    end

    x0=x;

    x=vpa(x,8)

end

x=vpa(x,8);

运行结果：取初值为2

k	xk	newton法	改进方法
1	x1	1.75	1.5
2	x2	1.5982143	1.4166667
3	x3	1.5115099	1.4142157
4	x4	1.4644275	1.4142157

计算4步，改进方法就已经收敛，而newton法只是线性收敛，要达到同样精度需迭代17次。

附结果：

>> [x,k]=budong(@biroot1,2,1e-5,3)

x =

1.5

x =

1.4166667

x =

1.4142157

x =

1.4142157

k =

>> [x,k]=budong(@biroot1,2,1e-5,10)

x =

1.5

x =

1.4166667

x =

1.4142157

x =

1.4142136

k =

>> [x,k]=budong(@newton_biroot,2,1e-5,50)

x =

1.75

x =

1.5982143

x =

1.5115099

x =

1.4644275

x =

1.439751

x =

1.4270955

x =

1.4206836

x =

1.4174559

x =

1.4158366

x =

1.4150256

x =

1.4146197

x =

1.4144166

x =

1.4143151

x =

1.4142643

x =

1.414239

x =

1.4142263

x =

1.4142199

k =