公钥密钥理解,signed cookie

公钥密钥理解,signed cookie

一、公钥密钥理解

公开密钥加密（英语：Public-key cryptography），也称为非对称加密（英语：asymmetric cryptography），是密码学的一种算法，它需要两个密钥，一个是公开密钥，另一个是私有密钥；一个用作加密的时候，另一个则用作解密。使用其中一个密钥把明文加密后所得的密文，只能用相对应的另一个密钥才能解密得到原本的明文；甚至连最初用来加密的密钥也不能用作解密。由于加密和解密需要两个不同的密钥，故被称为非对称加密；不同于加密和解密都使用同一个密钥的对称加密。虽然两个密钥在数学上相关，但如果知道了其中一个，并不能凭此计算出另外一个；因此其中一个可以公开，称为公钥，任意向外发布；不公开的密钥为私钥，必须由用户自行严格秘密保管，绝不通过任何途径向任何人提供，也不会透露给要通信的另一方，即使他被信任。

基于公开密钥加密的特性，它还提供数字签名的功能，使电子文件可以得到如同在纸本文件上亲笔签署的效果。

加密

如果任何人使用公钥加密明文，得到的密文可以通过不安全的途径（如网络）发送，只有对应的私钥持有者才可以解密得到明文；其他人即使从网络上窃取到密文及加密公钥，也无法（在数以年计的合理时间内）解密得出明文。典型例子是在网络银行或购物网站上，因为客户需要输入敏感消息，浏览器连接时使用网站服务器提供的公钥加密并上传数据，可保证只有信任的网站服务器才能解密得知消息，不必担心敏感个资因为在网络上传送而被窃取。

在现实世界上可作比拟的例子是，一个传统保管箱，开门和关门都是使用同一条钥匙，这是对称加密；而一个公开的邮箱，投递口是任何人都可以寄信进去的，这可视为公钥；而只有邮箱主人拥有钥匙可以打开邮箱，这就视为私钥。

非对称加密往往需要密码学安全伪随机数生成器的协助来产生一对密钥，

其中一个可以随便公开，称为公钥；另一个不公开，称为私钥，必须由用户自行严格秘密保管，绝不通过任何途径向任何人提供

加密过程

在数学上， d ( c ( x ) ) = x {\displaystyle d(c(x))=x} ，让我们使用典型的爱丽丝与鲍伯假设来解释：

1. 爱丽丝与鲍伯事先互不认识，也没有可靠安全的沟通渠道，但爱丽丝现在却要通过不安全的互联网向鲍伯发送信息
2. 爱丽丝撰写好原文，原文在未加密的状态下称之为明文 x {\displaystyle x}
3. 鲍伯使用密码学安全伪随机数生成器产生一对密钥，其中一个作为公钥为 c {\displaystyle c} ，另一个作为私钥 d {\displaystyle d}
4. 鲍伯可以用任何方法发送公钥 c {\displaystyle c} 给爱丽丝，即使伊夫在中间窃听到 c {\displaystyle c} 也没问题
5. 爱丽丝用公钥 c {\displaystyle c} 把明文 x {\displaystyle x} 进行加密，得到密文 c ( x ) {\displaystyle c(x)}
6. 爱丽丝可以用任何方法传输密文 c ( x ) {\displaystyle c(x)} 给鲍伯，即使伊夫在中间窃听到密文 c ( x ) {\displaystyle c(x)} 也没问题
7. 鲍伯收到密文，用私钥 d {\displaystyle d} 对密文进行解密 d ( c ( x ) ) {\displaystyle d(c(x))} ，得到爱丽丝撰写的明文 x {\displaystyle x}
8. 由于伊夫没有得到鲍伯的私钥 d {\displaystyle d} ，所以无法得知明文 x {\displaystyle x}
9. 如果爱丽丝丢失了她自己撰写的原文 x {\displaystyle x} ，在没有得到鲍伯的私钥 d {\displaystyle d} 的情况下，她的处境将等同伊夫，即无法通过鲍伯的公钥 c {\displaystyle c} 和密文 c ( x ) {\displaystyle c(x)} 重新得到原文 x {\displaystyle x}

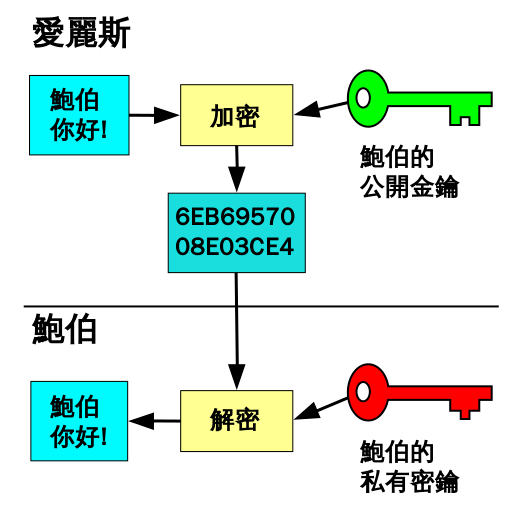
在非对称加密中，爱丽丝使用鲍伯的公钥加密明文，得到密文，而只有鲍伯因为持有私钥才可以解密，得到明文

数字签名

相反，如果某一用户使用他的私钥加密明文，任何人都可以用该用户的公钥解密密文；由于私钥只由该用户自己持有，故可以肯定该文件必定出自于该用户；公众可以验证该用户发布的数据或文件是否完整、中途有否曾被篡改，接收者可信赖这条信息确实来自于该用户，该用户亦无法抵赖，这被称作数字签名，大部分国家已经立法承认数字签名拥有等同传统亲笔签名的法律效力。公钥可以通过数字证书认证机构签授的电子证书形式公布，接收者通过信任链形成一套完整的公开密钥基础建设。例如，从网上下载的安装程序，一般都带有程序制作者的数字签名，可以证明该程序的确是该作者（公司）发布的而不是第三方伪造的且未被篡改过（身份认证/验证）。而在网络银行或购物网站，一般也会使用HTTPS，让客户确认他们不是连接到伪冒网站。

---

二、signed_cookie

cookie为了防止被恶意的客户端修改，用到了signed cookie.

比如cookie 是这样子authed:false 用户可以手动改成authed:true

这样是不安全的。所谓signed cookie是用到了 hash secret cookie_value

hash(cookie_value+secret)   发送的cookie 是authed:false|asdYTRESMcsgvsaw

false|asdYTRESMcsgvsaw 这堆随机字符串就是hash(cookie_value+secret)  后的结果

false|asdYTRESMcsgvsaw = hash(cookie_value+secret)

当cookie到达服务端时，将客户端发来的cookie_value与screate 哈希，如果与 false|asdYTRESMcsgvsaw 相等，则表明没有被篡改