[机器学习入门篇]-Logistic函数与Softmax函数

1.Logistic函数

在维基百科中，对logistic函数这样介绍道：

　　A logistic function or logistic curve is a common "S" shape (sigmoid curve), with equation: $$f(x)=\frac{L}{1+e^{-k(x-x0)}}$$

　　Logistic函数呈'S'型曲线，当x趋于-∞时函数趋于0，当x趋于+∞时函数趋于L。

2.Softmax函数

softmax函数定义如下：

　　In mathematics, the softmax function, or normalized exponential function,is a generalization of the logistic function that "squashes" a K-dimensional vector $\mathbf{Z}$ of arbitrary real values to a K-dimensional vector $\sigma(\textbf{Z})$ of real values in the range (0, 1) that add up to 1. The function is given by

　　$$\sigma(\textbf{Z})_j=\frac{e^Z_j}{\sum_{k=1}^{K}e^{Z_k}}\quad j=1,2,...,K$$

　　在数学定义中，Softmax函数是对Logistic函数的一般化。它的作用是将一个K维实数向量的各分量值映射到(0,1)，且各分量值之和为1。

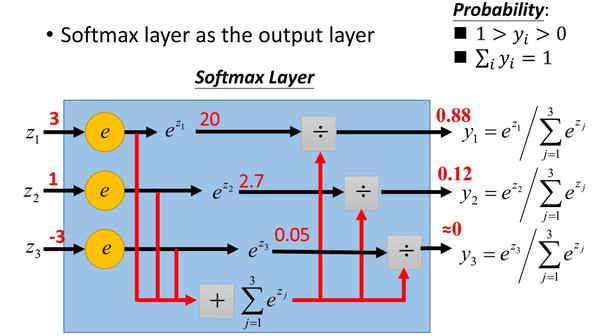
3.对比

从定义中不难看出，Softmax函数是对Logistic函数的延伸扩展。拿Sigmoid函数(Logistic函数的一种)为例，它将单个变量的取值变换到(0,1)，而Softmax函数是Sigmoid函数的多维形式，参数不是单个变量而是多维向量。由于维度不同，Logistic函数常被应用于回归问题(称为Logistic回归)和神经网络的激活函数。而Softmax函数常被用于神经网络的最后一层，进行多分类。

4.参考资料

更详细的介绍参考：http://www.cnblogs.com/maybe2030/p/5678387.html?utm_source=tuicool&utm_medium=referral

z {\displaystyle \mathbf {z} } of arbitrary real values to a K-dimensional vector σ ( z ) {\displaystyle \sigma (\mathbf {z} )} of real values in the range (0, 1) that add up to 1. The function is given by

σ ( z ) j = e z j ∑ k = 1 K e z k {\displaystyle \sigma (\mathbf {z} )_{j}={\frac {e^{z_{j}}}{\sum _{k=1}^{K}e^{z_{k}}}}}    for j = 1, …, K.