并查集【p2700】逐个击破

题目描述-->p2700 逐个击破

题意概括

花费最小的代价,使得一些有标记的节点不连通.

分析

我们需要花费最小代价使得原来连通的图中一些节点之间不相互连通.

贪心显然是可行的(一点也不显然

看到其他人写了dp,写了贪心.

但我感觉可以排序+并查集做啊.

排序

考虑我们要花费最小代价删边,但是并查集不支持删除操作.

(貌似有一种东西叫分治线段树可以维护这种操作.

因此,我们根据容斥原理(这玩意是叫容斥吧.

花费最小代价删边,等价于花最大代价建边,最后剩下不建的边,就是我们的答案.

所以说,我们需要按照边权从大到小建图。sort！

我们需要保证的是两个敌人节点不互相连通.

这就是我们并查集的作用!

并查集

首先明确：

并查集要初始化,一定要初始化!

下面的图中,红色代表敌人节点,绿色代表我方节点.

如果某两个节点是我们的敌人节点,我们一定不会去建边.(为虎作伥? 像这样↓.

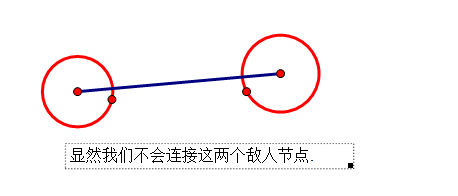
如果你连接,那你就违背了题目要求,你也不是一个

秉承伟大军事家的战略思想，一个有智慧的军长了

还有,如果我们已经将敌人包围建出下面这样的图这时,还有一个敌人节点.↓

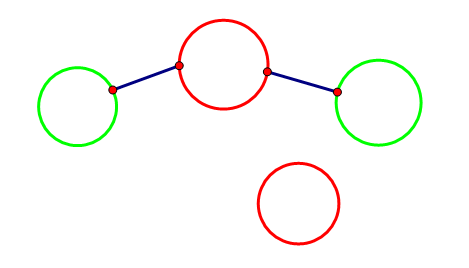
如果我们连接某一个我方节点,不连接敌方节点,那敌人也会互相连接(翻过屋后的山

所以说我们需要考虑一下如何解决这种情况.

如果,我方节点已经连接了敌方节点,则需要标记我方节点,使得敌方节点无法通过我方节点连接敌方节点.

因此说,我们可以把连接到敌人节点的我方节点变成敌人节点.

从而使得其他敌人节点与其无法连接.

那我们上面的图就变成这样↓

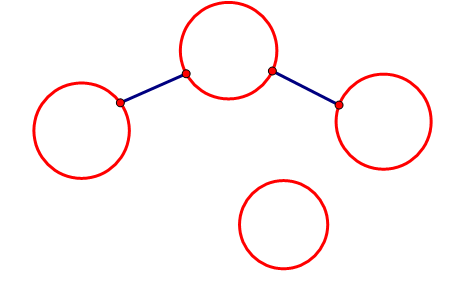
这样我们的程序就可以实现我们所想了.

最后我们会将边权大的边加入到并查集中.

则最后没有加入到并查集中的点,就会是被孤立的敌方节点.

所以我们把总边权减去我们加入到图中的边权就是我们的ans啦！

关于样例

样例建的原图↓

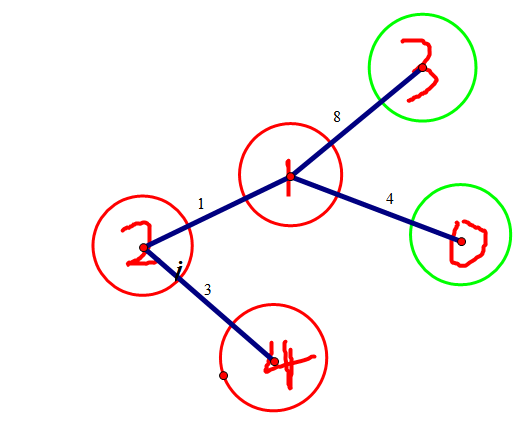
最终是这样的↓

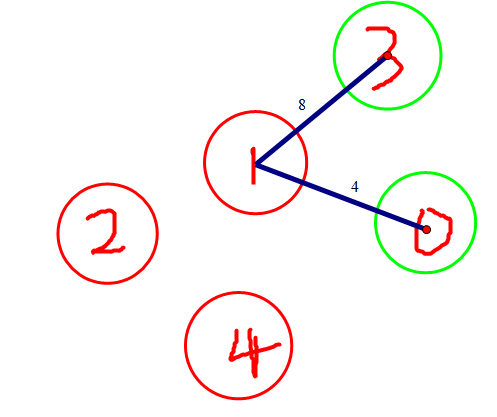
因此我们在样例的答案是4.

--------------------代码---------------------

#include<bits/stdc++.h>
#define IL inline
#define RI register int
IL void in(int &x)
{
	int f=1;x=0;char s=getchar();
	while(s>'9' or s<'0'){if(s=='-')f=-1;s=getchar();}
	while(s>='0' and s<='9'){x=x*10+s-'0';s=getchar();}
	x*=f;
}
int n,k,f[100008],tot;
bool init[1000008];
long long ans;
struct cod{int u,v,w;}edge[100008];
IL int find(int x){return f[x]==x?x:f[x]=find(f[x]);}
IL bool ccp(const cod&a,const cod&b){return a.w>b.w;}
int main(void)
{
	in(n),in(k);
	for(RI i=1;i<=n;i++)f[i]=i;//一定要初始化!
	for(RI i=1,x;i<=k;i++)in(x),init[x]=true;
	for(RI i=1;i<=n-1;i++)
		in(edge[i].u),in(edge[i].v),in(edge[i].w),ans+=edge[i].w;
	std::sort(edge+1,edge+n,ccp);//从大到小sort.
	for(RI i=1;i<=n-1;i++)
	{
		int u=edge[i].u,v=edge[i].v,w=edge[i].w;
		int fu=find(u),fv=find(v);
		if(init[fu] and init[fv])continue;
		f[fu]=fv;
		ans-=w;//减去边
		if(init[fu])init[fv]=true;
		else if(init[fv])init[fu]=true;
	}
	printf("%lld",ans);
}