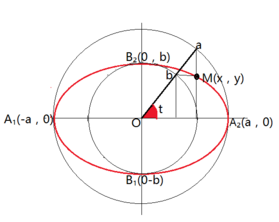
椭圆参数方程中的θ（离心角Theta）

椭圆参数方程中的离心角θ是交以其x轴对应外接圆上点的角度（或是交以其y轴对应内接圆上点的角度）

椭圆的参数程为：
x=acosθ
y=bsinθ.
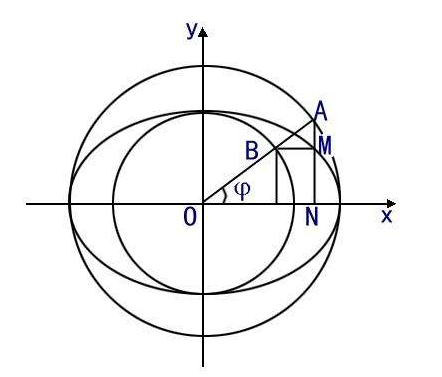
M(x,y)椭圆上一点。过M作直线⊥X轴，交以O为圆心，以a为半径的圆于B点，连接OB.
式中，θ----OB与X轴的正向的正夹角, a----椭圆的长半径，b----椭圆的短半径。

---

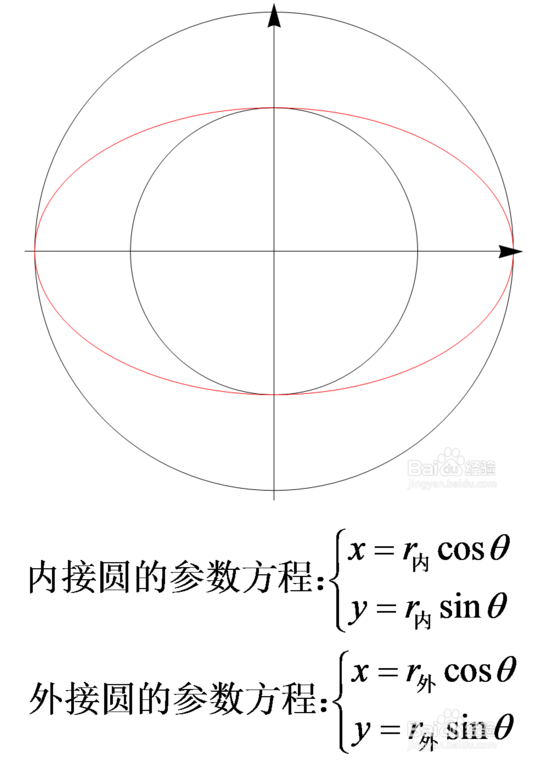
性质：内接圆和外接圆

分别以半短轴和半长轴为半径做椭圆的内接圆和外接圆

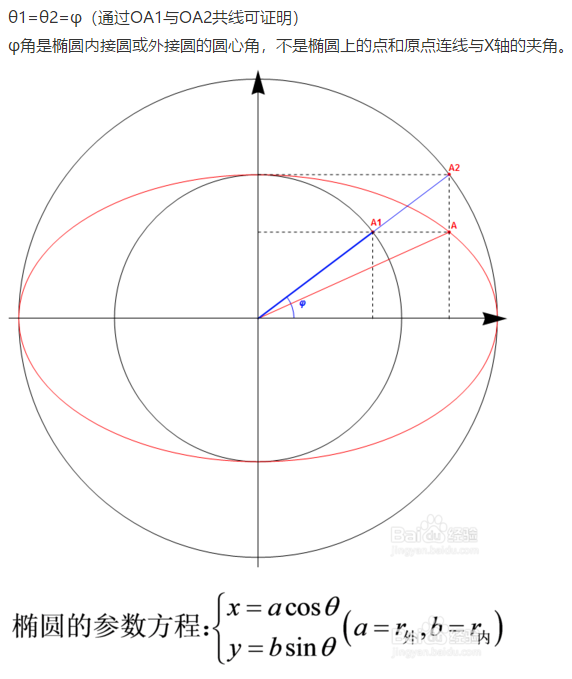
椭圆上的任意一点A与内接圆上的A1点有相同的纵坐标，与外接圆上的A2点有相同的横坐标。

【参考资料】

离心角_百度百科 https://baike.baidu.com/item/%E7%A6%BB%E5%BF%83%E8%A7%92/9589009?fr=aladdin

椭圆参数方程_百度经验 https://jingyan.baidu.com/article/22a299b5c193a99e19376abe.html