KMP算法细讲（豁然开朗）

一.KMP算法是如何针对传统算法修改的

用模式串P去匹配字符串S，在i=6,j=4时发生失配：

---------------------------------------------------------------------

i=6

S: a   b   a   b   c   a   d   c   a   c   b   a   b

P:           a   b   c   a   c

j=4

---------------------------------------------------------------------

此时，按照传统算法，应当将P的第 1 个字符 a(j=0) 滑动到与S中第4个字符 b(i=3) 对齐再进行匹配：

---------------------------------------------------------------------

i=3

S: a   b   a   b   c   a   a   d   a   c   b   a   b

P:          　  a   b   c   a   c

j=0

---------------------------------------------------------------------

这个过程中，对字符串S的访问发生了“回朔”（从 i=6 移回到 i=3）。

我们不希望发生这样的回朔，而是试图通过尽可能的“向右滑动”模式串P，让P中index为 j 的字符对齐到S中 i=5 的字符，然后试图匹配S中 i=6 的字符与P中index为 j+1 的字符。

在这个测试用例中，我们直接将P向右滑动3个字符，使S中 i=5 的字符与P中 j=0 的字符对齐，再匹配S中 i=6 的字符与P中 j=1 的字符。

---------------------------------------------------------------------

i=6

S: a   b   a   b   c   a   d   c   a   c   b   a   b

P:                  　　 a   b   c   a   c

j=0

---------------------------------------------------------------------

二.求KMP算法中的next

举例说明：

按上述定义给出next数组的一个例子：

j         0  1  2  3  4  5  6  7

P        a   b  a  a  b  c  a   c

next[j]  -1  0  0  1  1  2  0  1

查找对称串
申明一下：下面说的对称不是中心对称，而是中心字符块对称，比如不是abccba，而是abcabc这种对称。

详解：
将j导入next函数，即可求得，

j=0时，next[]=-1；

j=1时，k的取值为(,1)的开区间，所以整数k是不存在的，那就是第三种情况，next[]=；

j=2时，k的取值为（，）的开区间，k从最大的开始取值，然后带入含p的式子中验证等式是否成立，不成立k取第二大的值。现在是k=，将k导入p的式子中得，p0=p1，即“a”=“b”，
显然不成立，舍去。k再取值就超出范围了，所以next[]不属于第二种情况，那就是第三种了，即next[]=；

j=3时，k的取值为（，）的开区间，先取k=，将k导入p的式子中得，p0p1=p1p2，不成立。 再取k=，得p0=p2，成立。所以next[]=；

j=4时，k的取值为（，）的开区间，先取k=，将k导入p的式子中得，p0p1p2=p1p2p3，不成立。 再取k=，得p0p1=p2p3，不成立。 再取k=，得p0=p3，成立。所以next[]=；

……

在已知next数组的前提下，字符串匹配的步骤如下：

i 和 j 分别表示在主串S和模式串P中当前正待比较的字符

在匹配过程中的每一次循环，若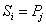，i 和 j 分别增 1，

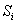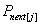else，j 退回到 next[j]的位置，此时下一次循环是与相比较。

void getnext(int *next, char *p)
{
    int j = , k = -;
    next[] = -;
    while(j < lenp-1)//-1
    {
        if(k == - || p[j] == p[k])
        {
            j++;
            k++;
            next[j] = k;//当j==0时，已经求出了next[1]的值，所以j<lenp-1
        }
        else
            k = next[k];
    }
}

三.getNext函数的进一步优化

注意到，上面的getNext函数还存在可以优化的地方，比如：

i=3

S: a   a   a   b   a   a   a   a   b

P: a   a   a   a   b

j=3

此时，i=3、j=3时发生失配，next[3]=2，此时还需要进行 3 次比较：

i=3, j=2;

i=3, j=1;

i=3, j=0。

而实际上，因为i=3, j=3时就已经知道a!=b，而之后的三次依旧是拿 a 和 b 比较，因此这三次比较都是多余的。

此时应当直接将P向右滑动4个字符，进行 i=4， j=0的比较。

一般而言，在getNext函数中，next[i]=j，也就是说当p[i]与S中某个字符匹配失败的时候，用p[j]继续与S中的这个字符比较。

如果p[i]==p[j]，那么这次比较是多余的（如同上面的例子），此时应该直接使next[i]=next[j]。

void getNextUpdate(const std::string& p, std::vector<int>& next)
{
    next.resize(p.size());
    next[] = -;

    int i = , j = -;

    while (i != p.size() - )
    {
        //这里注意，i==0的时候实际上求的是nextVector[1]的值，以此类推
        if (j == - || p[i] == p[j])
        {
            ++i;
            ++j;
            //update
            //next[i] = j;
            //注意这里是++i和++j之后的p[i]、p[j]
            next[i] = p[i] != p[j] ? j : next[j];
        }
        else
        {
            j = next[j];
        }
    }
}

假定p.size()为m，分析其时间复杂度的困惑在于，在while里面不是每次循环都执行 ++i 操作，所以整个while的执行次数不一定为m。

换个角度，注意到在每次循环中，无论 if 还是 else 都会修改 j 的值且每次循环仅对 j 进行一次修改，所以在整个while中 j 被修改的次数即为getNext函数的时间复杂度。

每次成功匹配时，++i; ++j; , 由于 ++i 最多执行 m-1 次，故++j也最多执行 m-1 次，即 j 最多增加m-1次；

对应的，只有在 j=next[j]; 处 j 的值一定会变小，由于 j 最多增加m-1次，故 j 最多减小m-1次。

综上所述，getNext函数的时间复杂度为O(m)，

若带匹配串S的长度为n，则kmp函数的时间复杂度为O(m+n)。（有待验证）

四、kmp的应用优势

①快，O(m+n)的线性最坏时间复杂度；

②无需回朔访问待匹配字符串S，所以对处理从外设输入的庞大文件很有效，可以边读入边匹配。

大部分转自GoAgent

http://www.cnblogs.com/goagent/archive/2013/05/16/3068442.html