[Contest20180321]nonintersect

$\dfrac 2\pi$是个引人注目的数字，先来看看它到底是什么东西

假如有一条直线，它和题目所给的某条长度为$d$的线段夹角为$\theta$，那么线段在直线上的投影长度为$\left|d\cos\theta\right|$

现在我们随机一条直线，于是线段的期望投影长度是$\dfrac{\int_0^\pi\left|d\cos\theta\right|d\theta}{\pi-0}=\dfrac2\pi d$

所以我们可以不停随机一个角度，把所有线段投影到这个角度的直线上，一旦检查到总投影长度与原长之比$\geq\dfrac2\pi$就停止

找（？）到合适的角度之后，我们按线段端点投影在直线上的横坐标把所有点分成左右两部分，找一种连线方法使得每条线端的两个端点一个在左边一个在右边，且连线不相交，这样就做完了这道题

当然一些细节是不得不讲的

①随机？问题不大...期望都是$\dfrac2\pi$了，想随机到一个比它大的一点都不难（这也顺带说明了不存在无解的情况）

②设原来线段总长为$len$，原来投影总长为$d$，求得答案的投影总长为$d'$，求得答案的线段总长为$len'$，那么显然有$\dfrac2\pi len\leq d$和$d'\leq len'$

考虑比较$d$和$d'$，我们要求答案的所有线段的端点分列左右两边，对应过来就是投影线段穿越中轴线，如果原来存在两条投影线段不穿越中轴线，我们换一种方式连接即可满足要求，这样一来投影长度还增加了，所以$d\leq d'$

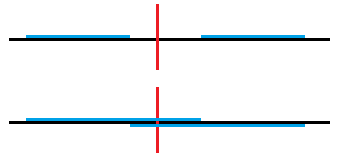
③怎么用合适的方法连线（不相交）

我们可以这样做：每次选取左半边的最左最下点，把其他点做极角排序，扫描的过程中统计扫描线下方左右两边的点数，一旦相同，连一条边并递归上下处理，这样就保证了连线不相交

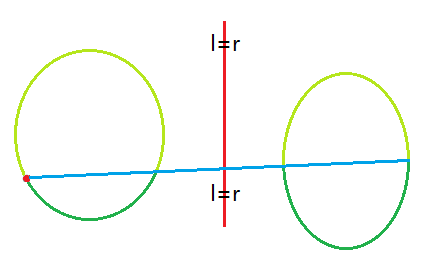
实现的时候可以不用写成递归的形式，对于分开的上下两组，分别打上不同的标记即可，下次处理到这里只需要找标记相同的点，跟递归差不多的意思gr

然后就做完了，挺愉悦的==

#include<stdio.h>
#include<math.h>
#include<algorithm>
using namespace std;
const double pi=3.141592653589793238462643383;
struct point{
	double x,y;
	point(double a=0,double b=0){x=a;y=b;}
}p[10010],a[10010];
double dis(point a,point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}
int match[10010],id[10010],s[10010],c[10010],bl[10010];
bool v[10010];
double ang[10010];
bool cmpx(int x,int y){return a[x].x<a[y].x||(a[x].x==a[y].x&&a[x].y<a[y].y);}
bool cmpa(int x,int y){return ang[x]<ang[y];}
int main(){
	int n,i,j,k,x,y,l,c0,c1,tot;
	double sum,tmp,d,dx,dy;
	scanf("%d",&n);
	for(i=1;i<=n<<1;i++)scanf("%lf%lf",&p[i].x,&p[i].y);
	sum=0;
	for(i=1;i<=n;i++){
		scanf("%d%d",&x,&y);
		sum+=dis(p[x],p[y]);
	}
	while(1){
		d=(rand()%10000)/10000.*2*pi;
		dx=cos(d);
		dy=sin(d);
		for(i=1;i<=n<<1;i++)a[i]=point(p[i].x*dx-p[i].y*dy,p[i].x*dy+p[i].y*dx);
		for(i=1;i<=n<<1;i++)id[i]=i;
		sort(id+1,id+(n<<1|1),cmpx);
		tmp=0;
		for(i=1;i<=n;i++)tmp+=a[id[i+n]].x-a[id[i]].x;
		if(tmp>=2/pi*sum)break;
	}
	for(i=1;i<=n;i++){
		s[id[i]]=0;
		s[id[i+n]]=1;
	}
	tot=0;
	for(i=1;i<=n;i++){
		x=id[i];
		v[x]=1;
		l=0;
		for(j=1;j<=n<<1;j++){
			if(!v[j]&&bl[j]==bl[x]){
				ang[j]=atan2(a[j].y-a[x].y,a[j].x-a[x].x);
				l++;
				c[l]=j;
			}
		}
		sort(c+1,c+l+1,cmpa);
		c0=c1=0;
		for(j=1;j<=l;j++){
			y=c[j];
			if(s[x]!=s[y]&&c0==c1){
				match[x]=y;
				match[y]=x;
				v[y]=1;
				tot++;
				for(k=1;k<j;k++)bl[c[k]]=tot;
				break;
			}
			if(s[y])
				c1++;
			else
				c0++;
		}
	}
	for(i=1;i<=n<<1;i++){
		if(match[i]>i)printf("%d %d\n",i,match[i]);
	}
}