12.25模拟赛T1

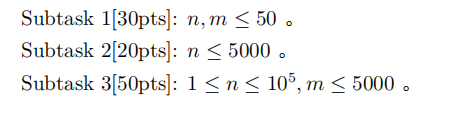
可以区间dp，但是复杂度太高。

所以应该是贪心，怎么贪心呢？

这种题目，最好还是手玩找一些规律。

可以发现，由于保证可以m次填完，所以颜色之间没有相互包含关系。

比较像分治的模型。

所以考虑拿到一个区间怎么处理。

假设a[l]==a[r]，那么为了合法，一定先刷这种颜色。然后分部分递归下去。

否则，对于区间：AEEGEABBBCDDC

里面的夹心肯定不能先处理了，可以大概看做：A..AB..BC..C

先刷哪一个？

刷两边长度较小的一个

证明：

如果刷中间，那么中间的位置之后就不能再动了。如果刷比较长的一个，那么之后不能再动。

如果刷比较短的一个，长的可以再多刷几次，贡献更大。

比较即可。（如果两边长度相同，比较下一个。）

O(m^2+n)

理论上可以后缀数组优化到：O(mlogn+n)

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=1e5;
const int M=;
int st[M],nd[M];
ll ans;
int a[N];
int n,m;
vector<int>mem[M];
void sol(int l,int r){
    //cout<<" sol "<<l<<" "<<r<<" "<<ans<<endl;
    if(l>r) return;
    if(l==r){
        ++ans;return;
    }
    if(a[l]==a[r]){
        ans+=r-l+;
        int las=l;
        for(reg i=;i<mem[a[l]].size();++i){
            sol(las+,mem[a[l]][i]-);
            las=mem[a[l]][i];
        }
    }
    else{
        int L=l,R=r;
        int go=;
        ans+=r-l+;
        while(!go){
            if(nd[a[L]]-st[a[L]]+<nd[a[R]]-st[a[R]]+){
                go=l;break;
            }else if(nd[a[L]]-st[a[L]]+>nd[a[R]]-st[a[R]]+){
                go=r;break;
            }
            L=nd[a[L]]+;R=st[a[R]]-;
            if(L>R) go=l;
        }
        if(go==l){
            int las=l;
            for(reg i=;i<mem[a[l]].size();++i){
                sol(las+,mem[a[l]][i]-);
                las=mem[a[l]][i];
            }
            sol(las+,r);
        }else{
            int las=st[a[r]];
            for(reg i=;i<mem[a[r]].size();++i){
                sol(las+,mem[a[r]][i]-);
                las=mem[a[r]][i];
            }
            sol(l,st[a[r]]-);
        }
    }
}
int main(){
    rd(n);rd(m);
    for(reg i=;i<=n;++i){
        rd(a[i]);
        if(st[a[i]]==) st[a[i]]=i;
        nd[a[i]]=i;
        mem[a[i]].push_back(i);
    }
    sol(,n);
    printf("%lld",ans);
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2018/12/25 15:04:11
*/

总结：

没有想到的原因是，还是没有从手玩找规律这个方向入手。

对于一些没有什么思路的题，可以尝试“不完全归纳”

其实规律还是比较简单的。