CF 305B——Continued Fractions——————【数学技巧】

B. Continued Fractions

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

A continued fraction of height n is a fraction of form 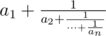. You are given two rational numbers, one is represented as  and the other one is represented as a finite fraction of height n. Check if they are equal.

Input

The first line contains two space-separated integers p, q (1 ≤ q ≤ p ≤ 1018) — the numerator and the denominator of the first fraction.

The second line contains integer n (1 ≤ n ≤ 90) — the height of the second fraction. The third line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 1018) — the continued fraction.

Please, do not use the %lld specifier to read or write 64-bit integers in С++. It is preferred to use the cin, cout streams or the %I64d specifier.

Output

Print "YES" if these fractions are equal and "NO" otherwise.

Sample test(s)

input

9 4
2
2 4

output

YES

input

9 4
3
2 3 1

output

YES

input

9 4
3
1 2 4

output

NO

Note

In the first sample .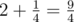

In the second sample .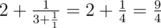

In the third sample .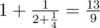

题目大意：判断两个式子是不是相等。

解题思路：p=q*a+r（a表示商，r表示余数）。则可以每次判断p-q*ai（相当于ai后边的分式的结果）的值是否小于0，如果小于0，说明肯定是不等的；如果大于0，将q当做p，将（p-q*ai）当做q（p、q的转变，表示将后边的一串分式取倒数）重复上边的过程。

#include<bits/stdc++.h>
using namespace std;
#define LL long long
LL a[100];
LL gcd(LL a,LL b){
    return b?gcd(b,a%b):a;
}
int main(){
    LL p,q,tm;
    int n,i,j,k;
    while(scanf("%I64d%I64d",&p,&q)!=EOF){

        scanf("%d",&n);
        bool flag=0;
        for(i=0;i<n;i++){
            scanf("%I64d",&a[i]);
            if(flag==1){
                continue;
            }
            if(p/q<a[i]){
                flag=1;
                continue;
            }
            tm=q;
            q=p-q*a[i];
            if(q<=0&&i!=n-1){
                flag=1;
                continue;
            }
            p=tm;
            tm=gcd(p,q);
            p/=tm;
            q/=tm;
        }
        if(q>0)
            flag=1;
        if(flag==1){
            printf("NO\n");
        }else{
            printf("YES\n");
        }
    }
    return 0;
}