bzoj 2154 Crash的数字表格（莫比乌斯反演及优化）

Description

今天的数学课上，Crash小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数a和b，LCM(a, b)表示能同时被a和b整除的最小正整数。例如，LCM(6, 8) = 24。回到家后，Crash还在想着课上学的东西，为了研究最小公倍数，他画了一张N*M的表格。每个格子里写了一个数字，其中第i行第j列的那个格子里写着数为LCM(i, j)。一个4*5的表格如下： 1 2 3 4 5 2 2 6 4 10 3 6 3 12 15 4 4 12 4 20 看着这个表格，Crash想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题：这个表格中所有数的和是多少。当N和M很大时，Crash就束手无策了，因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大，Crash只想知道表格里所有数的和mod 20101009的值。

Input

输入的第一行包含两个正整数，分别表示N和M。

Output

输出一个正整数，表示表格中所有数的和mod 20101009的值。

Sample Input

4 5

Sample Output

122
【数据规模和约定】
100%的数据满足N, M ≤ 107。

 

【思路】

 

　　这个博客推倒过程挺详细的 click here

　　我是图片的搬运工

　　

　　

　　到此为止，只要两个循环都用个分块就可以解决2154了。

 

【代码】

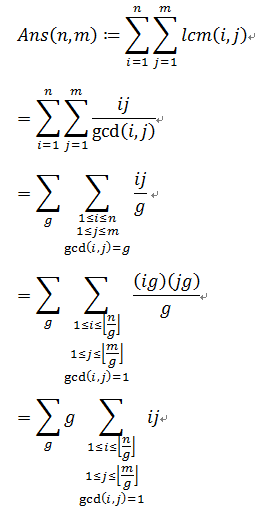
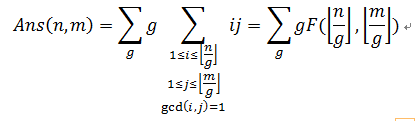
 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;

 typedef long long ll;
 const int N = 1e7+;
 const int MOD = ;

 ll mu[N],su[N],sz,np[N];
 int n,m,mx;

 void get_mu()
 {
     int i,j;
     mu[]=;
     for(i=;i<=mx;i++) {
         if(!np[i])
             su[++sz]=i,mu[i]=-;
         for(j=;j<=sz&&i*su[j]<=mx;j++) {
             np[i*su[j]]=;
             if(i%su[j]==)
                 mu[i*su[j]]=;
             else
                 mu[i*su[j]]=-mu[i];
         }
     }
     for(i=;i<=mx;i++)
         mu[i]=(mu[i-]+(ll)(mu[i]*i*i)%MOD)%MOD;
 }
 ll t(ll x,ll y)
 {
     return ((ll)(x*(x+)/%MOD)*(ll)(y*(y+)/%MOD)%MOD);
 }
 ll F(int n,int m)
 {
     int i,last; ll ans=;
     for(i=;i<=n;i=last+) {
         last=min(n/(n/i),m/(m/i));
         ans=(ans+(ll)(mu[last]-mu[i-])*t(n/i,m/i)%MOD)%MOD;
     }
     return ans;
 }
 int main()
 {
     //freopen("in.in","r",stdin);
     //freopen("out.out","w",stdout);
     scanf("%d%d",&n,&m);
     if(n>m) swap(n,m);
     mx=n;
     get_mu();
     int last; ll ans=;
     for(int i=;i<=n;i=last+) {
         last=min(n/(n/i),m/(m/i));
         ans=(ans+((ll)(i+last)*(last-i+)/*F(n/i,m/i)%MOD))%MOD;
     }
     printf("%lld",(ans+MOD)%MOD);
     return ;
 }

【优化】

　　我是图片的搬运工

　　

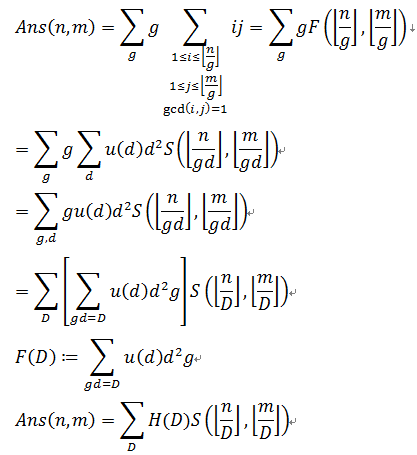
　　（H打错为F 233）

　　积性函数的约数和也是积性函数，H(D) 可以用线性筛求，然后求下前缀和就好了。

　　至此为止，可以解决2693的多查询问题了。

 

【代码】

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;

 typedef long long ll;
 const int N = 1e7+;
 const int MOD = ;

 ll sum[N],su[N],sz,np[N];
 int n,m,mx;

 void get_mu()
 {
     int i,j;
     sum[]=;
     for(i=;i<=mx;i++) {
         if(!np[i]) {
             su[++sz]=i,
             sum[i]=(i-(ll)i*i)%MOD;
         }
         for(j=;j<=sz&&i*su[j]<=mx;j++) {
             np[i*su[j]]=;
             if(i%su[j]==)
                 sum[i*su[j]]=(su[j]*sum[i])%MOD;
             else
                 sum[su[j]*i]=(sum[su[j]]*sum[i])%MOD;
         }
     }
     for(i=;i<=mx;i++)
         sum[i]=(sum[i]+sum[i-])%MOD;
 }
 ll S(ll x,ll y)
 {
     return ((ll)(x*(x+)/%MOD)*(ll)(y*(y+)/%MOD)%MOD);
 }

 int main()
 {
     //freopen("in.in","r",stdin);
     //freopen("out.out","w",stdout);
     mx=1e7;
     get_mu();
     int T; scanf("%d",&T);
     while(T--) {
         scanf("%d%d",&n,&m);
         if(n>m) swap(n,m);
         mx=n; get_mu();
         int last; ll ans=;
         for(int i=;i<=n;i=last+) {
             last=min(n/(n/i),m/(m/i));
             ans=(ans+(ll)S(n/i,m/i)*(sum[last]-sum[i-])%MOD)%MOD;
         }
         printf("%lld\n",(ans+MOD)%MOD);
     }
     return ;
 }

　　两倍经验get :)

　　最后扔上popoqqq神犇的ppt click here