POJ1179Polygon(DP)

Polygon

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4456		Accepted: 1856

Description

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.


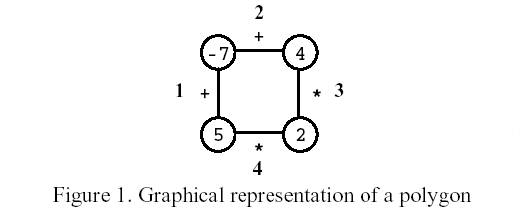
On the first move, one of the edges is removed. Subsequent moves involve the following steps:

�pick an edge E and the two vertices V1 and V2 that are linked by E; and

�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.

The game ends when there are no more edges, and its score is the label of the single vertex remaining.

Consider the polygon of Figure 1. The player started by removing
edge 3. After that, the player picked edge 1, then edge 4, and, finally,
edge 2. The score is 0.



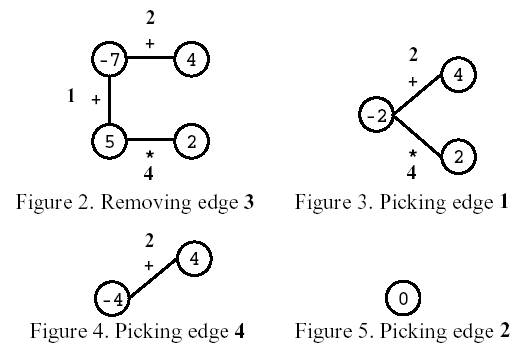
Write a program that, given a polygon, computes the highest possible
score and lists all the edges that, if removed on the first move, can
lead to a game with that score.

Input

Your
program is to read from standard input. The input describes a polygon
with N vertices. It contains two lines. On the first line is the number
N. The second line contains the labels of edges 1, ..., N, interleaved
with the vertices' labels (first that of the vertex between edges 1 and
2, then that of the vertex between edges 2 and 3, and so on, until that
of the vertex between edges N and 1), all separated by one space. An
edge label is either the letter t (representing +) or the letter x
(representing *).

3 <= N <= 50

For any sequence of moves, vertex labels are in the range [-32768,32767].

Output

Your
program is to write to standard output. On the first line your program
must write the highest score one can get for the input polygon. On the
second line it must write the list of all edges that, if removed on the
first move, can lead to a game with that score. Edges must be written in
increasing order, separated by one space.

Sample Input

4
t -7 t 4 x 2 x 5

Sample Output

33
1 2

题目的意思就是给n个数，n个两两数之间的运算符（只有+和*）问首先去掉哪个运算符号之后可以让其他的数按照一定的方法计算后结果最大。
其实结题思路还是比较好想到的，枚举（枚举去掉的符号）+DP（记忆化搜索）就可以做到。但这里有一个天坑，就是负负得正，所以不能单一的枚举最大值，而要同时DP最小值。        
计算最大值：
   加法  max(i,j) = max(i,k)+max(k,j);
   乘法  max(i,j) = MAX(max（i,k）*max(k,j),max(i,k)*min(k,j),max(k,j)*min(i,k),min(i,k)*min(k,j));(i=<k<=j)
计算最小值：

   加法  min(i,j) = min(i,k)+min(k,j);
   乘法  min(i,j) = MIN(max（i,k）*max(k,j),min(i,k)*min(k,j),max(k,j)*min(i,k),min(i,k)*min(k,j));(i=<k<=j)

见代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <stack>
#include <set>
#include <queue>
#define MAX(a,b) (a) > (b)? (a):(b)
#define MIN(a,b) (a) < (b)? (a):(b)
#define mem(a) memset(a,0,sizeof(a))
#define INF 1000000007
#define MAXN 20005
using namespace std;

bool op[];
int num[],dp_max[], dp_min[], n;
bool vis_max[],vis_min[];
int DP_MIN(int i,int j);
int DP_MAX(int i,int j);

int DP_MAX(int i,int j)//DP求区间最大值
{
    int u = i*+j;
    if(vis_max[u])return dp_max[u];
    vis_max[u]=;
    if(j-i <= )
    {
        if(j==i)return dp_max[u]=num[i-];
        if(!op[i])return dp_max[u]=num[i-]+num[i];
        else return dp_max[u]=num[i-]*num[i];
    }
    dp_max[u] = -INF;
    for(int k=i;k<j;k++)
    {
        int l=DP_MIN(i,k);
        int r=DP_MIN(k+,j);
        int ll=DP_MAX(i,k);
        int rr=DP_MAX(k+,j);
        if(!op[k])dp_max[u] = MAX(dp_max[u], ll+rr);
        else dp_max[u] = MAX(dp_max[u], MAX(ll*rr,MAX(l*r,MAX(l*rr,r*ll))));
    }
    return dp_max[u];
}

int DP_MIN(int i,int j)//DP求区间最小值
{
    int u = i*+j;
    if(vis_min[u])return dp_min[u];
    vis_min[u]=;
    if(j-i <= )
    {
        if(j==i)return dp_min[u]=num[i-];
        if(!op[i])return dp_min[u]=num[i-]+num[i];
        else return dp_min[u]=num[i-]*num[i];
    }
    dp_min[u] = INF;
    for(int k=i;k<j;k++)
    {
        int l=DP_MIN(i,k);
        int r=DP_MIN(k+,j);
        int ll=DP_MAX(i,k);
        int rr=DP_MAX(k+,j);
        if(!op[k])dp_min[u] = MIN(dp_min[u], l+r);
        else dp_min[u] = MIN(dp_min[u], MIN(ll*rr,MIN(l*r,MIN(l*rr,r*ll))));
    }
    return dp_min[u];
}

int main()
{
    while(~scanf("%d%*c",&n))
    {
        mem(op);mem(dp_max);
        mem(num);mem(vis_min);
        mem(vis_max);
        int max=-INF,i;
        char ch;
        for(i=;i<n;i++)
        {
            scanf("%c %d%*c",&ch,&num[i]);
            op[i]=op[i+n]=(ch=='x');
            num[i+n]=num[i];
        }
        for(i=;i<n;i++)
        {
            max=MAX(max,DP_MAX(i+,i+n));
        }
        printf("%d\n",max);
        int ok=;
        for(i=;i<n;i++)
        {
            if(DP_MAX(i+,i+n) == max)
            {
                if(ok){printf("%d",i+);ok=;}
                else printf(" %d",i+);
            }
        }
        printf("\n");
    }
    return ;
}