并查集（UVA 1106）

POINT：

　　把每个元素看成顶点，则一个简单化合物就是一条无向边,若存在环（即k对组合中有k种元素），则危险，不应该装箱，反之，装箱；

　　用一个并查集维护连通分量集合，每次得到一种化合物(x, y)时检查x, y是否在同一集合中，如果是，拒绝，反之接受。

并查集

　　并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。

　　集就是让每个元素构成一个单元素的集合，也就是按一定顺序将属于同一组的元素所在的集合合并。

---------------------------------------------------------------------------------------------------------

以下转自：http://www.cnblogs.com/cyjb/p/UnionFindSets.html，3Q~

---------------------------------------------------------------------------------------------------------

　　并查集（Union-find Sets）是一种非常精巧而实用的数据结构，它主要用于处理一些不相交集合的合并问题。一些常见的用途有求连通子图、求最小生成树的 Kruskal 算法和求最近公共祖先（Least Common Ancestors, LCA）等。

　　使用并查集时，首先会存在一组不相交的动态集合 ，一般都会使用一个整数表示集合中的一个元素。

　　每个集合可能包含一个或多个元素，并选出集合中的某个元素作为代表。每个集合中具体包含了哪些元素是不关心的，具体选择哪个元素作为代表一般也是不关心的。我们关心的是，对于给定的元素，可以很快的找到这个元素所在的集合（的代表），以及合并两个元素所在的集合，而且这些操作的时间复杂度都是常数级的。

并查集的基本操作有三个：

1. makeSet(s)：建立一个新的并查集，其中包含 s 个单元素集合。
2. unionSet(x, y)：把元素 x 和元素 y 所在的集合合并，要求 x 和 y 所在的集合不相交，如果相交则不合并。
3. find(x)：找到元素 x 所在的集合的代表，该操作也可以用于判断两个元素是否位于同一个集合，只要将它们各自的代表比较一下就可以了。

　　并查集的实现原理也比较简单，就是使用树来表示集合，树的每个节点就表示集合中的一个元素，树根对应的元素就是该集合的代表，如图 1 所示。

　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　图 1 并查集的树表示

　　图中有两棵树，分别对应两个集合，其中第一个集合为 {a, b, c, d}, 代表元素是a; 第二个集合为{e, f, g}, 代表元素是ee。

　　树的节点表示集合中的元素，指针表示指向父节点的指针，根节点的指针指向自己，表示其没有父节点。沿着每个节点的父节点不断向上查找，最终就可以找到该树的根节点，即该集合的代表元素。

　　现在，应该可以很容易的写出 makeSet 和 find 的代码了，假设使用一个足够长的数组来存储树节点（很类似之前讲到的静态链表），那么 makeSet 要做的就是构造出如图 2 的森林，其中每个元素都是一个单元素集合，即父节点是其自身：

　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　图 2 构造并查集初始化

相应的代码如下所示，时间复杂度是 0(n)：

 const int MAXSIZE = ;
 int uset[MAXSIZE];

 void makeSet(int size)
 {
     for(int i = ;i < size;i++) uset[i] = i;
 }

接下来，就是 find 操作了，如果每次都沿着父节点向上查找，那时间复杂度就是树的高度，完全不可能达到常数级。这里需要应用一种非常简单而有效的策略——路径压缩。

路径压缩，就是在每次查找时，令查找路径上的每个节点都直接指向根节点，如图 3 所示。

　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　图 3 路径压缩

我准备了两个版本的 find 操作实现，分别是递归版和非递归版，不过两个版本目前并没有发现有什么明显的效率差距，所以具体使用哪个完全凭个人喜好了。

 int find(int x)
 {
     if (x != uset[x])
          uset[x] = find(uset[x]);
     return uset[x];
 }

 int find(int x)
 {
     int p = x, t;
     while (uset[p] != p)
         p = uset[p];
     while (x != p)
     {
         t = uset[x]; uset[x] = p; x = t;
     }
     return x;
 }        

最后是合并操作 unionSet，并查集的合并也非常简单，就是将一个集合的树根指向另一个集合的树根，如图 4 所示。

　　　　　　　　

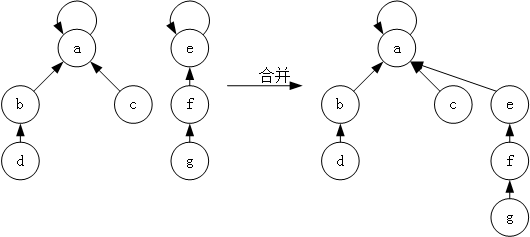
　　　　　　　　　　　　　　　　　　　　　　图 4 并查集的合并

这里也可以应用一个简单的启发式策略——按秩合并。该方法使用秩来表示树高度的上界，在合并时，总是将具有较小秩的树根指向具有较大秩的树根。简单的说，就是总是将比较矮的树作为子树，添加到较高的树中。为了保存秩，需要额外使用一个与 uset 同长度的数组，并将所有元素都初始化为 0。

1 2 3 4 5 6 7 8

void unionSet(int x, int y) {     if ((x = find(x)) == (y = find(y))) return;     if (rank[x] > rank[y]) uset[y] = x;     else {         uset[x] = y;         if (rank[x] == rank[y]) rank[y]++;     } }

下面是按秩合并的并查集的完整代码，这里只包含了递归的 find 操作。

const int MAXSIZE = 500;

int uset[MAXSIZE];

int rank[MAXSIZE];

 

void makeSet(int size) {

    for(int i = 0;i < size;i++)  uset[i] = i;

    for(int i = 0;i < size;i++)  rank[i] = 0;

}

int find(int x) {

    if (x != uset[x]) uset[x] = find(uset[x]);

    return uset[x];

}

void unionSet(int x, int y) {

    if ((x = find(x)) == (y = find(y))) return;

    if (rank[x] > rank[y]) uset[y] = x;

    else {

        uset[x] = y;

        if (rank[x] == rank[y]) rank[y]++;

    }

}

除了按秩合并，并查集还有一种常见的策略，就是按集合中包含的元素个数（或者说树中的节点数）合并，将包含节点较少的树根，指向包含节点较多的树根。这个策略与按秩合并的策略类似，同样可以提升并查集的运行速度，而且省去了额外的 rank 数组。

这样的并查集具有一个略微不同的定义，即若 uset 的值是正数，则表示该元素的父节点（的索引）；若是负数，则表示该元素是所在集合的代表（即树根），而且值的相反数即为集合中的元素个数。相应的代码如下所示，同样包含递归和非递归的 find 操作：

const int MAXSIZE = 500;

int uset[MAXSIZE];

 

void makeSet(int size) {

    for(int i = 0;i < size;i++) uset[i] = -1;

}

int find(int x) {

    if (uset[x] < 0) return x;

    uset[x] = find(uset[x]);

    return uset[x];

}

int find(int x) {

    int p = x, t;

    while (uset[p] >= 0) p = uset[p];

    while (x != p) {

        t = uset[x];

        uset[x] = p;

        x = t;

    }

    return x;

}

void unionSet(int x, int y) {

    if ((x = find(x)) == (y = find(y))) return;

    if (uset[x] < uset[y]) {

        uset[x] += uset[y];

        uset[y] = x;

    } else {

        uset[y] += uset[x];

        uset[x] = y;

    }

}

如果要获取某个元素 x 所在集合包含的元素个数，可以使用 -uset[find(x)] 得到。

并查集的空间复杂度是O(n)的，这个很显然，如果是按秩合并的，占的空间要多一些。find 和 unionSet 操作都可以看成是常数级的，或者准确来说，在一个包含 n 个元素的并查集中，进行 m 次查找或合并操作，最坏情况下所需的时间为 O(mα(n))，这里的α是 Ackerman 函数的某个反函数，在极大的范围内（比可观察到的宇宙中估计的原子数量 10^80 还大很多）都可以认为是不大于 4 的。具体的时间复杂度分析，请参见《算法导论》的 21.4 节 带路径压缩的按秩合并的分析。

作者：CYJB
出处：http://www.cnblogs.com/cyjb/

GitHub：https://github.com/CYJB/

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。

-----------------------------------分割线------------------------------------

  #include <iostream>
 #include <sstream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <string>
 #include <vector>
 #include <set>
 #include <cctype>
 #include <algorithm>
 #include <cmath>
 #include <deque>
 #include <queue>
 #include <map>
 #include <stack>
 #include <list>
 #include <iomanip>
 using namespace std;

 #define INF 0xffffff7
 #define maxn 100000+10

 int pa[maxn];

 void makeset(int size)
 {
     for(int i = ; i < size; i++)
         pa[i] = i;
 }

 int findset(int x)//并查集的查找操作，带路径压缩
 {
     return pa[x] != x ? pa[x] = findset(pa[x]) : x;
 }

 int main()
 {
     int cnt = ;
     int m, n, k = ;
     while(scanf("%d", &m) != EOF)
     {
         makeset(maxn);

         int refusals = ;
         while(m != -)
         {
             scanf("%d", &n);
             m = findset(m); n = findset(n);//执行后m, n分别是两个集合的代表元素
             if(m == n)  ++refusals; //如果m, n代表同一集合，则拒绝
             else pa[m] = n; //否则合并，（不是启发式合并）
             scanf("%d", &m);
         }
         printf("%d\n", refusals);
     }

     return ;
 }