Guass列选主元消去法和三角分解法

　　最近数值计算学了Guass列主消元法和三角分解法解线性方程组，具体原理如下：

1、Guass列选主元消去法对于AX =B

1）、消元过程：将（A|B）进行变换为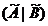，其中是上三角矩阵。即：

k从1到n-1

a、 列选主元

选取第k列中绝对值最大元素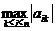作为主元。

b、 换行

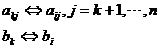
c、 归一化

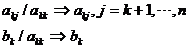
d、 消元

2）、回代过程：由解出。

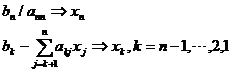
2、三角分解法（Doolittle分解）

将A分解为如下形式

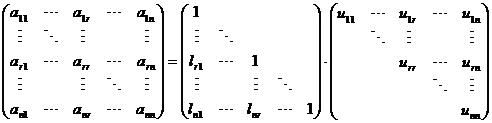
由矩阵乘法原理

a、计算U的第一行，再计算L的第一列

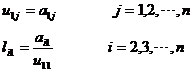
b、设已求出U的1至r-1行，L的1至r-1列。先计算U的第r行，再计算L的第r列。

a）计算U的r行

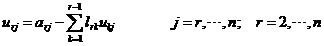
b）计算L的r列

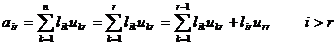
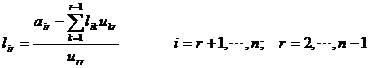
C#代码：

　　代码说明：Guass列主消元法部分将计算出来的根仍然储存在增广矩阵的最后一列，而Doolittle分解，将分解后的结果也储存至原来的数组中，这样可以节约空间。。

using System;
using System.Windows.Forms;

namespace Test
{
    public partial class Form1 : Form
    {
        public Form1()
        {
            InitializeComponent();
        }

        private void Cannel_Button_Click(object sender, EventArgs e)
        {
            this.textBox1.Clear();
            this.textBox2.Clear();
            this.textBox3.Clear();
            this.comboBox1.SelectedIndex = -1;
        }
        public double[,] GetNum(string str, int n)
        {
            string[] strnum = str.Split(' ');
            double[,] a = new double[n, n + 1];
            int k = 0;
            for (int i = 0; i < n; i++)
            {
                for (int j = 0; j < strnum.Length / n; j++)
                {
                    a[i, j] = double.Parse((strnum[k]).ToString());
                    k++;
                }
            }
            return a;
        }
        public void Gauss(double[,] a, int n)
        {
            int i, j;
            SelectColE(a, n);
            for (i = n - 1; i >= 0; i--)
            {
                for (j = i + 1; j < n; j++)
                    a[i, n] -= a[i, j] * a[j, n];
                a[i, n] /= a[i, i];
            }
        }
        //选择列主元并进行消元
        public void SelectColE(double[,] a, int n)
        {
            int i, j, k, maxRowE;
            double temp; //用于记录消元时的因数
            for (j = 0; j < n; j++)
            {
                maxRowE = j;
                for (i = j; i < n; i++)
                    if (System.Math.Abs(a[i, j]) > System.Math.Abs(a[maxRowE, j]))
                        maxRowE = i;
                if (maxRowE != j)
                    swapRow(a, j, maxRowE, n);   //与最大主元所在行交换
                                                 //消元
                for (i = j + 1; i < n; i++)
                {
                    temp = a[i, j] / a[j, j];
                    for (k = j; k < n + 1; k++)
                        a[i, k] -= a[j, k] * temp;
                }
            }
            return;
        }
        public void swapRow(double[,] a, int m, int maxRowE, int n)
        {
            int k;
            double temp;
            for (k = m; k < n + 1; k++)
            {
                temp = a[m, k];
                a[m, k] = a[maxRowE, k];
                a[maxRowE, k] = temp;
            }
        }
        public void Doolittle(double[,] a, int n)
        {
            for (int i = 0; i < n; i++)
            {
                if (i == 0)
                {
                    for (int j = i + 1; j < n; j++)
                        a[j, 0] = a[j, 0] / a[0, 0];
                }
                else
                {
                    double temp = 0, s = 0;
                    for (int j = i; j < n; j++)
                    {
                        for (int k = 0; k < i; k++)
                        {
                            temp = temp + a[i, k] * a[k, j];
                        }
                        a[i, j] = a[i, j] - temp;
                    }
                    for (int j = i + 1; j < n; j++)
                    {
                        for (int k = 0; k < i; k++)
                        {
                            s = s + a[j, k] * a[k, i];
                        }
                        a[j, i] = (a[j, i] - s) / a[i, i];
                    }
                }
            }
        }
        private void Exit_Button_Click(object sender, EventArgs e)
        {
            this.Close();
        }

        private void Confirm_Button_Click(object sender, EventArgs e)
        {
            if (this.textBox2.Text.Trim().ToString().Length == 0)
            {
                this.textBox2.Text = this.textBox1.Text.Trim();
            }
            else
            {
                this.textBox2.Text = this.textBox2.Text + "\r\n" + this.textBox1.Text.Trim();
            }
            this.textBox1.Clear();
        }

        private void Calculate_Button_Click(object sender, EventArgs e)
        {
            string str = this.textBox2.Text.Trim().ToString();
            string myString = str.Replace("\n", " ").Replace("\r", string.Empty);
            double[,] a = new double[this.textBox2.Lines.GetUpperBound(0) + 1, this.textBox2.Lines.GetUpperBound(0) + 2];
            a = GetNum(myString, this.textBox2.Lines.GetUpperBound(0) + 1);
            if (this.comboBox1.Text == "Guass列主消元法")
            {
                Gauss(a, this.textBox2.Lines.GetUpperBound(0) + 1);
                for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++)
                {
                    this.textBox3.Text = this.textBox3.Text + "\r\nX" + (i + 1) + "=" + a[i, this.textBox2.Lines.GetUpperBound(0) + 1];
                }
            }
            else if (this.comboBox1.Text == "Doolittle三角分解法")
            {
                this.textBox3.Enabled = true;
                Doolittle(a, this.textBox2.Lines.GetUpperBound(0) + 1);
                this.label3.Text = "分解后的结果：";
                this.textBox3.Clear();
                this.textBox3.Text += "L矩阵：\r\n";
                for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++)
                {
                    for (int j = 0; j < this.textBox2.Lines.GetUpperBound(0) + 1; j++)
                    {
                        if (j < i)
                        {
                            this.textBox3.Text += a[i, j].ToString() + "\t";
                        }
                        else if (i == j)
                        {
                            this.textBox3.Text += "1\t";
                        }
                        else
                        {
                            this.textBox3.Text += "0\t";
                        }
                    }
                    this.textBox3.Text += "\r\n";
                }
                this.textBox3.Text += "\r\nU矩阵：\r\n";
                for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++)
                {
                    for (int j = 0; j < this.textBox2.Lines.GetUpperBound(0) + 1; j++)
                    {
                        if (j >= i)
                        {
                            this.textBox3.Text += a[i, j].ToString() + "\t";
                        }
                        else
                        {
                            this.textBox3.Text += "0\t";
                        }
                    }
                    this.textBox3.Text += "\r\n";
                }
            }

        }

        private void textBox1_KeyDown(object sender, KeyEventArgs e)
        {
            if (e.KeyCode == Keys.Enter)
            {
                if (this.textBox1.Text.Trim().ToString().Length == 0)
                {
                    Calculate_Button_Click(sender, e);
                }
                else
                {
                    Confirm_Button_Click(sender, e);
                }
            }
        }
        private void button1_Click(object sender, EventArgs e)
        {
            this.textBox2.Enabled = true;
        }
    }
}

　　运行截图：

　　至此完毕。。。。