P3368 【模板】树状数组 2（树状数组维护差分序列）

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数数加上x

2.求出某一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含2或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x 含义：输出第x个数的值

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

输出样例#1：

6
10

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

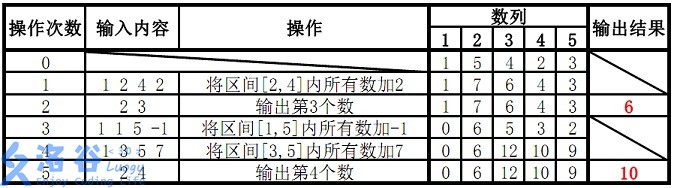
故输出结果为6、10

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 using namespace std;
 int lowbit(int x)
 {return x&-x;}
 void read(int & n)
 {
     char c='+';int x=;bool flag=;
     while(c<''||c>'')
     {c=getchar();if(c=='-')flag=;}
     while(c>=''&&c<='')
     {x=x*+(c-),c=getchar();}
     flag==?n=-x:n=x;
 }
 const int MAXN=;
 int c[MAXN],n,m,p,x,y,z,pre;
 void add(int p,int v)
 {
     while(p<=n)
     {
         c[p]+=v;
         p+=lowbit(p);
     }
 }
 int ask(int p)
 {
     int ans=;
     while(p>)
     {
         ans+=c[p];
         p-=lowbit(p);
     }
     return ans;
 }
 int main()
 {
     read(n);read(m);
     for(int i=;i<=n;i++)
     {
         read(p);
         add(i,p-pre);
         pre=p;
     }

     while(m--)
     {
         read(p);
         if(p==)// 区间加
         {
             read(x);read(y);read(z);
             add(x,z);
             add(y+,-z);
         }
         else// 单点查询
         {
             read(x);
             printf("%d\n",ask(x));
         }
     }
     return ;
 }