BZOJ 4085 丧心病狂的毒瘤题目 线段树+矩乘

思路：

一眼矩阵快速幂 再用线段树维护一下矩阵就完了...

我hhhhh    哎我还是too young,too simple 入了这个大坑

线段树维护9个值

以上

如果A+1   转移矩阵是这个样子的

B+1

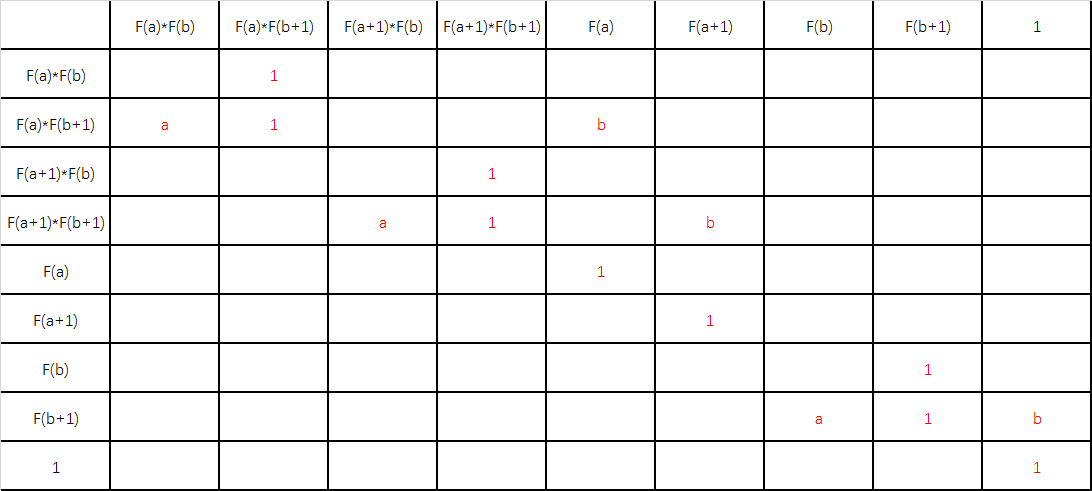
A-1 B-1 同理行么.....

写了一晚上+一上午  调完了

发现自己被卡常？

我了个大曹

我们发现一开始的矩阵最后一行不变

矩乘的时候特判一发  还是过不去

预处理2^k的矩阵

快速幂的时候省一倍常数  加个快读

80432 ms

卡过去了！！

//By SiriusRen
#include <bits/stdc++.h>
using namespace std;
const int mod=,N=;
int n,q,a,b,A[N],F[N],d[N][],lazy[N*][];
inline int read(){
    int x=;char p=getchar();
    while(p<''||p>'')p=getchar();
    while(p>=''&&p<='')x=x*+p-'',p=getchar();
    return x;
}
struct MATRIX{
    int a[][];
    void init(){memset(a,,sizeof(a));}
}t[],t0;
int pow(int x,int y){
    int res=;
    while(y){
        if(y&)res=1ll*res*x%mod;
        x=1ll*x*x%mod,y>>=;
    }return res;
}
MATRIX operator*(MATRIX &a,MATRIX &b){
    static MATRIX c;c.init();
    for(int i=;i<;i++)
        for(int j=;j<;j++){
            for(int k=;k<;k++)
                c.a[i][j]=(c.a[i][j]+1ll*a.a[i][k]*b.a[k][j])%mod;
        }
    c.a[][]=;
    return c;
}
MATRIX power(int k){
    static MATRIX res;res.init();
    res.a[][]=res.a[][]=res.a[][]=;
    for(int i=;k;k>>=,i++)if(k&)res=res*t[i];
    return res;
}
struct Matrix{
    int m[][];
    void init(){memset(m,,sizeof(m));}
    void init1(){
        int B[][]={
            {,,,,,,,,},
            {,,,,,,,,},
            {a,,,,,,b,,},
            {,a,,,,,,b,},
            {,,,,,,,,},
            {,,,,a,,,,b},
            {,,,,,,,,},
            {,,,,,,,,},
            {,,,,,,,,},
        };
        memcpy(m,B,sizeof(B));
    }
    void init2(){
        int B[][]={
            {,,,,,,,,},
            {a,,,,b,,,,},
            {,,,,,,,,},
            {,,a,,,b,,,},
            {,,,,,,,,},
            {,,,,,,,,},
            {,,,,,,,,},
            {,,,,,,a,,b},
            {,,,,,,,,},
        };
        memcpy(m,B,sizeof(B));
    }
    void init3(){
        int x,y,z;
        if(a){
            int inv=pow(a,mod-);
            x=inv,y=mod-inv,z=1ll*b*(mod-inv)%mod;
        }
        else x=,y=,z=mod-b;
        int B[][]={
            {y,,x,,,,z,,},
            {,y,,x,,,,z,},
            {,,,,,,,,},
            {,,,,,,,,},
            {,,,,y,x,,,z},
            {,,,,,,,,},
            {,,,,,,,,},
            {,,,,,,,,},
            {,,,,,,,,},
        };
        memcpy(m,B,sizeof(B));
    }
    void init4(){
        int x,y,z;
        if(a){
            int inv=pow(a,mod-);
            x=inv,y=mod-inv,z=1ll*b*(mod-inv)%mod;
        }
        else x=,y=,z=mod-b;
        int B[][]={
            {y,x,,,z,,,,},
            {,,,,,,,,},
            {,,y,x,,z,,,},
            {,,,,,,,,},
            {,,,,,,,,},
            {,,,,,,,,},
            {,,,,,,y,x,z},
            {,,,,,,,,},
            {,,,,,,,,},
        };
        memcpy(m,B,sizeof(B));
    }
}cng[][],I;
Matrix operator*(Matrix &a,Matrix &b){
    Matrix c;c.init();
    for(int i=;i<;i++)
        for(int j=;j<;j++){
            for(int k=;k<;k++)
                c.m[i][j]=(c.m[i][j]+1ll*a.m[i][k]*b.m[k][j])%mod;
        }
    return c;
}
void bz(){
    cng[][].init1();cng[][].init2();
    cng[][].init3();cng[][].init4();
    for(int i=;i<;i++){
        cng[i][]=I;
        for(int j=;j<=;j++)
            cng[i][j]=cng[i][j-]*cng[i][j-];
    }
}
struct Line{
    int m[];
    void set(int aa_1,int aa,int bb_1,int bb){
        m[]=1ll*aa_1*bb_1%mod,m[]=1ll*aa_1*bb%mod,m[]=1ll*aa*bb_1%mod,
        m[]=1ll*aa*bb%mod,m[]=aa_1,m[]=aa,m[]=bb_1,m[]=bb,m[]=;
    }
}tr[<<],ans;
Line operator+(Line &a,Line &b){
    Line c;
    for(int i=;i<;i++)c.m[i]=(a.m[i]+b.m[i])%mod;
    return c;
}
Line operator*(Matrix &a,Line &b){
    Line c;memset(c.m,,sizeof(c.m));
    for(int i=;i<;i++)
        for(int j=;j<;j++)
            c.m[i]=(c.m[i]+1ll*a.m[i][j]*b.m[j])%mod;
    return c;
}
void change(Line &f,Matrix r[],int k){
    for(int i=;k;k>>=,i++)if(k&)f=r[i]*f;
}
void calc(int pos,int a0,int a1){
    if(a0){
        if(a0<)change(tr[pos],cng[],-a0);
        else change(tr[pos],cng[],a0);
    }
    if(a1){
        if(a1<)change(tr[pos],cng[],-a1);
        else change(tr[pos],cng[],a1);
    }
}
void push_down(int pos,int l,int r){
    calc(pos,lazy[pos][],lazy[pos][]);
    if(l<r){
        int lson=pos<<,rson=pos<<|;
        lazy[lson][]+=lazy[pos][],lazy[lson][]+=lazy[pos][];
        lazy[rson][]+=lazy[pos][],lazy[rson][]+=lazy[pos][];
    }
    lazy[pos][]=lazy[pos][]=;
}
void push_up(int pos,int l,int r){
    int mid=(l+r)>>,lson=pos<<,rson=pos<<|;
    push_down(lson,l,mid),push_down(rson,mid+,r);
    tr[pos]=tr[lson]+tr[rson];
}
void build(int l,int r,int pos){
    if(l==r){
        tr[pos].set(d[l-][],d[l-][],d[r+][],d[r+][]);
        return;
    }
    int mid=(l+r)>>,lson=pos<<,rson=pos<<|;
    build(l,mid,lson),build(mid+,r,rson);
    push_up(pos,l,r);
}
void insert(int l,int r,int pos,int L,int R,int op){
    if(L>R)return;
    if(l>=L&&r<=R){
        if(!op)lazy[pos][]++;
        else if(op==)lazy[pos][]++;
        else if(op==)lazy[pos][]--;
        else if(op==)lazy[pos][]--;
        return;
    }push_down(pos,l,r);
    int mid=(l+r)>>,lson=pos<<,rson=pos<<|;
    if(mid<L)insert(mid+,r,rson,L,R,op);
    else if(mid>=R)insert(l,mid,lson,L,R,op);
    else insert(l,mid,lson,L,R,op),insert(mid+,r,rson,L,R,op);
    push_up(pos,l,r);
}
void query(int l,int r,int pos,int L,int R){
    if(L>R)return;
    push_down(pos,l,r);
    if(l>=L&&r<=R){ans=ans+tr[pos];return;}
    int mid=(l+r)>>,lson=pos<<,rson=pos<<|;
    if(mid<L)query(mid+,r,rson,L,R);
    else if(mid>=R)query(l,mid,lson,L,R);
    else query(l,mid,lson,L,R),query(mid+,r,rson,L,R);
}
signed main(){
    scanf("%d%d%d%d",&n,&q,&a,&b);
    for(int i=;i<;i++)I.m[i][i]=;
    t[].a[][]=t[].a[][]=t[].a[][]=,t[].a[][]=a,t[].a[][]=b;
    t0.a[][]=t0.a[][]=,t0.a[][]=;
    for(int i=;i<=;i++)t[i]=t[i-]*t[i-];
    for(int i=;i<=n;i++){
        A[i]=read();
        if(A[i]!=){
            MATRIX temp=power(A[i]-);temp=temp*t0;
            d[i][]=temp.a[][],d[i][]=temp.a[][];
        }
        else d[i][]=,d[i][]=;
        d[i][]=(d[i][]+1ll*d[i][]*a+b)%mod;
        d[i][]=(d[i][]+1ll*d[i][]*a+b)%mod;
    }bz(),build(,n-,);
    while(q--){
        char op[];int l,r;
        scanf("%s%d%d",op,&l,&r);
        if(op[]=='q'){
            memset(ans.m,,sizeof(ans.m));
            query(,n-,,l+,r-);
            printf("%d\n",ans.m[]);
        }
        else if(op[]=='p')insert(,n-,,l+,min(n-,r+),),insert(,n-,,max(l-,),r-,);
        else insert(,n-,,l+,min(n-,r+),),insert(,n-,,max(l-,),r-,);
    }
}