Minimum Path Sum(DFS,DP)

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

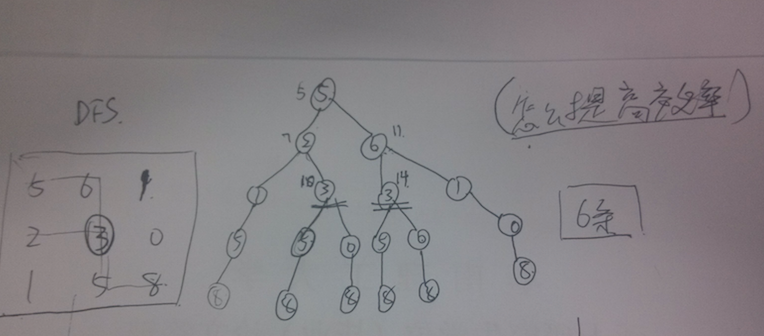
解法1：DFS，超时。

思路：其实类似对二叉树的DFS，只是终止条件不同，递归的终止条件就是到达最后一列，或者到达最后一行，因为最后一列的数字只有一个选择就是往下走，最后一行类似只有往右走。

当走到grid[rowMax-1][colMax-1]，也就是一次路径完成，并和minSum做较，取较小的。

超时输入：

int my_grid[rowMax][colMax]={

{7,1,3,5,8,9,9,2,1,9,0,8,3,1,6,6,9,5},
{9,5,9,4,0,4,8,8,9,5,7,3,6,6,6,9,1,6},
{8,2,9,1,3,1,9,7,2,5,3,1,2,4,8,2,8,8},
{6,7,9,8,4,8,3,0,4,0,9,6,6,0,0,5,1,4},
{7,1,3,1,8,8,3,1,2,1,5,0,2,1,9,1,1,4},
{9,5,4,3,5,6,1,3,6,4,9,7,0,8,0,3,9,9},
{1,4,2,5,8,7,7,0,0,7,1,2,1,2,7,7,7,4},
{3,9,7,9,5,8,9,5,6,9,8,8,0,1,4,2,8,2},
{1,5,2,2,2,5,6,3,9,3,1,7,9,6,8,6,8,3},
{5,7,8,3,8,8,3,9,9,8,1,9,2,5,4,7,7,7},
{2,3,2,4,8,5,1,7,2,9,5,2,4,2,9,2,8,7},
{0,1,6,1,1,0,0,6,5,4,3,4,3,7,9,6,1,9}};

代码：

class Solution {
private:
    int minSum;
    vector<vector<int>> my_grid;
    int rowMax;
    int colMax;
public:
    void tra(int i,int j,int sum){
        sum+=my_grid[i][j];
        if(j==colMax-&&i<rowMax)
        {
            ++i;
            for (i;i<rowMax;++i)
            {
                sum+=my_grid[i][j];
            }
            if(i==rowMax&&sum<minSum){
                minSum=sum;
            }
            return;
        }
        if(i==rowMax-&&j<colMax)
        {
            ++j;
            for (j;j<colMax;++j)
            {
                sum+=my_grid[i][j];
            }
            if(j==colMax&&sum<minSum){
                minSum=sum;
            }
            return;
        }
        tra(i,j+,sum);
        tra(i+,j,sum);
    }
    int minPathSum(vector<vector<int>>& grid) {
        minSum=(~(unsigned int))>>;
        my_grid=grid;
        rowMax=grid.size();
        colMax=grid[].size();
        tra(,,);
        return minSum;
    }

};

解法2：DP（还是不熟练，不太熟练递推dp和递归dp的区别，参考文章）

dp[100][100];该dp数组记录的是每个位置上的最优解，即到达这一点的路径最小值。假设我们要求以grid[i][j]为末尾的最小路径值，我们只需要求出它头上一个格子，和左边格子为末尾的最小路径值之中的最小值，也即min{dp[i-1][j],dp[i][j-1]}.

所以综合下，动态转移方程就是dp[i][j]=min{dp[i-1][j],dp[i][j-1]}+grid[i][j];

代码：

class Solution {
public:
    int minPathSum(vector<vector<int> > &grid) {
        if(grid.size()==)
            return ;
        vector<vector<int>> res(grid);
        int i, j;
        for(int j=; j<res[].size(); ++j){
            res[][j] += res[][j-];
        }
        for(int j=; j<res.size(); ++j){
            res[j][] += res[j-][];
        }
        for(i=; i<res.size(); ++i){
            for(int j=; j<res[i].size(); ++j){
                res[i][j] = min(res[i-][j], res[i][j-])+grid[i][j];
            }
        }
        return res[grid.size()-][grid[].size()-];    //注意行列的size不一定一样
    }
};