向量自回归模型VS风险价值模型(VAR&VaR)
单从外观上看,VAR&VaR两个模型很容易混淆,但就模型方法和用处两者截然不同,R语言作为数据分析的有力工具,其函数包库中包含各种各样的统计模型。通过vars包可以调用向量自回归模型,通过PerformanceAnalytics包的VaR函数可以调用风险价值模型。
模型简介
library(vars)
- 向量自回归模型(Vector Autoregression),简称VAR模型,是一种常用的计量经济模型,由克里斯托弗·西姆斯(Christopher Sims)提出。VAR模型是用模型中所有当期变量对所有变量的若干滞后变量进行回归。VAR模型用来估计联合内生变量的动态关系,而不带有任何事先约束条件。它是AR模型的推广,此模型目前已得到广泛应用。
library(PerformanceAnalytics)=>VaR()
- 风险价值模型(Value at Risk),通常被称作VaR方法。VaR按字面的解释就是“处于风险状态的价值”,即在一定置信水平和一定持有期内,某一金融资产或其组合在未来资产价格波动下所面临的最大损失额。JP.Morgan定义为:VaR是在既定头寸被冲销(be neutraliged)或重估前可能发生的市场价值最大损失的估计值;而Jorion则把VaR定义为:“给定置信区间的一个持有期内的最坏的预期损失”。
向量自回归模型(Vector Autoregression)
VAR模型R语言实例:
library(vars)
library(astsa) #数据包
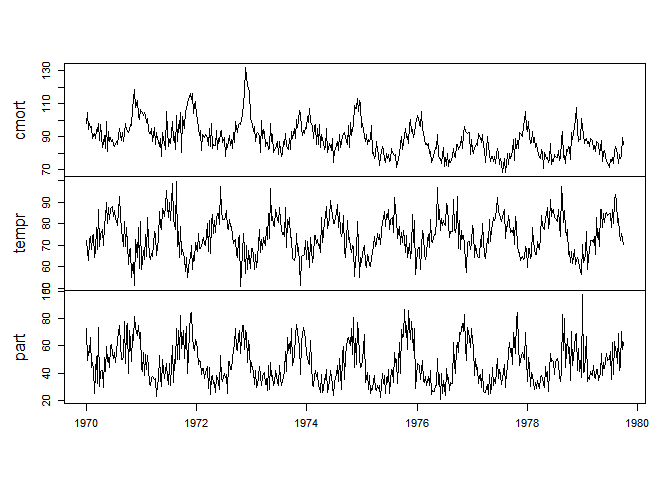
x = cbind(cmort, tempr, part)
plot.ts(x , main = "", xlab = "")
summary(VAR(x, p=1, type="both"))
##
## VAR Estimation Results:
## =========================
## Endogenous variables: cmort, tempr, part
## Deterministic variables: both
## Sample size: 507
## Log Likelihood: -5116.02
## Roots of the characteristic polynomial:
## 0.8931 0.4953 0.1444
## Call:
## VAR(y = x, p = 1, type = "both")
##
##
## Estimation results for equation cmort:
## ======================================
## cmort = cmort.l1 + tempr.l1 + part.l1 + const + trend
##
## Estimate Std. Error t value Pr(>|t|)
## cmort.l1 0.464824 0.036729 12.656 < 2e-16 ***
## tempr.l1 -0.360888 0.032188 -11.212 < 2e-16 ***
## part.l1 0.099415 0.019178 5.184 3.16e-07 ***
## const 73.227292 4.834004 15.148 < 2e-16 ***
## trend -0.014459 0.001978 -7.308 1.07e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 5.583 on 502 degrees of freedom
## Multiple R-Squared: 0.6908, Adjusted R-squared: 0.6883
## F-statistic: 280.3 on 4 and 502 DF, p-value: < 2.2e-16
##
##
## Estimation results for equation tempr:
## ======================================
## tempr = cmort.l1 + tempr.l1 + part.l1 + const + trend
##
## Estimate Std. Error t value Pr(>|t|)
## cmort.l1 -0.244046 0.042105 -5.796 1.20e-08 ***
## tempr.l1 0.486596 0.036899 13.187 < 2e-16 ***
## part.l1 -0.127661 0.021985 -5.807 1.13e-08 ***
## const 67.585598 5.541550 12.196 < 2e-16 ***
## trend -0.006912 0.002268 -3.048 0.00243 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 6.4 on 502 degrees of freedom
## Multiple R-Squared: 0.5007, Adjusted R-squared: 0.4967
## F-statistic: 125.9 on 4 and 502 DF, p-value: < 2.2e-16
##
##
## Estimation results for equation part:
## =====================================
## part = cmort.l1 + tempr.l1 + part.l1 + const + trend
##
## Estimate Std. Error t value Pr(>|t|)
## cmort.l1 -0.124775 0.079013 -1.579 0.115
## tempr.l1 -0.476526 0.069245 -6.882 1.77e-11 ***
## part.l1 0.581308 0.041257 14.090 < 2e-16 ***
## const 67.463501 10.399163 6.487 2.10e-10 ***
## trend -0.004650 0.004256 -1.093 0.275
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 12.01 on 502 degrees of freedom
## Multiple R-Squared: 0.3732, Adjusted R-squared: 0.3683
## F-statistic: 74.74 on 4 and 502 DF, p-value: < 2.2e-16
##
##
##
## Covariance matrix of residuals:
## cmort tempr part
## cmort 31.172 5.975 16.65
## tempr 5.975 40.965 42.32
## part 16.654 42.323 144.26
##
## Correlation matrix of residuals:
## cmort tempr part
## cmort 1.0000 0.1672 0.2484
## tempr 0.1672 1.0000 0.5506
## part 0.2484 0.5506 1.0000
风险价值模型(Value at Risk)
VaR模型R语言实例:
library(PerformanceAnalytics)
data(edhec)
# first do normal VaR calc
VaR(edhec, p=.95, method="historical")
## Convertible Arbitrage CTA Global Distressed Securities
## VaR -0.01916 -0.0354 -0.018875
## Emerging Markets Equity Market Neutral Event Driven
## VaR -0.044605 -0.006385 -0.02254
## Fixed Income Arbitrage Global Macro Long/Short Equity Merger Arbitrage
## VaR -0.00929 -0.01624 -0.02544 -0.013455
## Relative Value Short Selling Funds of Funds
## VaR -0.013175 -0.07848 -0.021265
# now use Gaussian
VaR(edhec, p=.95, method="gaussian")
## Convertible Arbitrage CTA Global Distressed Securities
## VaR -0.02645782 -0.03471098 -0.0221269
## Emerging Markets Equity Market Neutral Event Driven
## VaR -0.05498927 -0.008761813 -0.02246202
## Fixed Income Arbitrage Global Macro Long/Short Equity Merger Arbitrage
## VaR -0.01900198 -0.02023018 -0.02859264 -0.01152478
## Relative Value Short Selling Funds of Funds
## VaR -0.01493049 -0.08617027 -0.02393888
# now use modified Cornish Fisher calc to take non-normal distribution into account
VaR(edhec, p=.95, method="modified")
## Convertible Arbitrage CTA Global Distressed Securities
## VaR -0.03247395 -0.03380228 -0.0274924
## Emerging Markets Equity Market Neutral Event Driven
## VaR -0.06363081 -0.01134637 -0.02812515
## Fixed Income Arbitrage Global Macro Long/Short Equity Merger Arbitrage
## VaR -0.0246791 -0.01548247 -0.03037494 -0.01486869
## Relative Value Short Selling Funds of Funds
## VaR -0.01926435 -0.07431463 -0.02502852
# now use p=.99
VaR(edhec, p=.99)
## Convertible Arbitrage CTA Global Distressed Securities
## VaR -0.1009223 -0.04847019 -0.06533764
## Emerging Markets Equity Market Neutral Event Driven
## VaR -0.1397195 -0.04404136 -0.06385154
## Fixed Income Arbitrage Global Macro Long/Short Equity Merger Arbitrage
## VaR -0.05850228 -0.02437999 -0.05508705 -0.03630211
## Relative Value Short Selling Funds of Funds
## VaR -0.050531 -0.122236 -0.05500037
# or the equivalent alpha=.01
VaR(edhec, p=.01)
## Convertible Arbitrage CTA Global Distressed Securities
## VaR -0.1009223 -0.04847019 -0.06533764
## Emerging Markets Equity Market Neutral Event Driven
## VaR -0.1397195 -0.04404136 -0.06385154
## Fixed Income Arbitrage Global Macro Long/Short Equity Merger Arbitrage
## VaR -0.05850228 -0.02437999 -0.05508705 -0.03630211
## Relative Value Short Selling Funds of Funds
## VaR -0.050531 -0.122236 -0.05500037
# now with outliers squished
VaR(edhec, clean="boudt")
## Convertible Arbitrage CTA Global Distressed Securities
## VaR -0.0192821 -0.03380228 -0.02281122
## Emerging Markets Equity Market Neutral Event Driven
## VaR -0.05335613 -0.006583541 -0.02588255
## Fixed Income Arbitrage Global Macro Long/Short Equity Merger Arbitrage
## VaR -0.01947099 -0.01612116 -0.02997413 -0.01255334
## Relative Value Short Selling Funds of Funds
## VaR -0.0147671 -0.07881339 -0.02474761
# add Component VaR for the equal weighted portfolio
VaR(edhec, clean="boudt", portfolio_method="component")
## $MVaR
## [,1]
## [1,] 0.01206124
##
## $contribution
## Convertible Arbitrage CTA Global Distressed Securities
## 1.189614e-03 7.392667e-05 1.380388e-03
## Emerging Markets Equity Market Neutral Event Driven
## 3.044882e-03 3.255042e-04 1.633369e-03
## Fixed Income Arbitrage Global Macro Long/Short Equity
## 1.122597e-03 9.551128e-04 1.725166e-03
## Merger Arbitrage Relative Value Short Selling
## 5.594788e-04 9.422577e-04 -2.647415e-03
## Funds of Funds
## 1.756359e-03
##
## $pct_contrib_MVaR
## Convertible Arbitrage CTA Global Distressed Securities
## 0.098631120 0.006129276 0.114448260
## Emerging Markets Equity Market Neutral Event Driven
## 0.252451840 0.026987629 0.135422963
## Fixed Income Arbitrage Global Macro Long/Short Equity
## 0.093074804 0.079188612 0.143033874
## Merger Arbitrage Relative Value Short Selling
## 0.046386511 0.078122792 -0.219497771
## Funds of Funds
## 0.145620091
反馈与建议
- 作者:ShangFR
- 邮箱:shangfr@foxmail.com
向量自回归模型VS风险价值模型(VAR&VaR)的更多相关文章
- VAR向量自回归模型学习笔记2
向量自回归模型 今天的你 和昨天的你 和前天的你,是否具有相关性. 1. 定义 向量自回归(VAR,Vector Auto regression)分析联合内生变量间的动态关系 联合:n个变量间的相互影 ...
- 《Interest Rate Risk Modeling》阅读笔记——第十章 主成分模型与 VaR 分析
目录 第十章:主成分模型与 VaR 分析 思维导图 一些想法 推导 PCD.PCC 和 KRD.KRC 的关系 PCD 和 KRD PCC 和 KRC 第十章:主成分模型与 VaR 分析 思维导图 一 ...
- 用户价值模型 CITE :https://www.jianshu.com/p/34199b13ffbc
RFM用户价值模型的原理和应用 ▌定义 在众多的用户价值分析模型中,RFM模型是被广泛被应用的:RFM模型是衡量客户价值和客户创利能力的重要工具和手段,在RFM模式中,R(Recency)表示客户购 ...
- 数据分析之客户价值模型(RFM)技术总结
作者 | leo 管理学中有一个重要概念那就是客户关系管理(CRM),它核心目的就是为了提高企业的核心竞争力,通过提高企业与客户间的交互,优化客户管理方式,从而实现吸引新客户.保留老客户以及将已有客户 ...
- VAR模型学习笔记
目录 1 定义 VAR模型的具体步骤 建模步骤及公式 代码实现 1 定义 VAR模型除了分析自身滞后项的影响外,还分析其他相关因素的滞后项对未来值产生的影响参考 用来分析随机扰动对系统的动态冲击的大小 ...
- 市场风险~VaR的概述
1.概念理解 VaR的含义:Value at Risk 按字面的解释就是"处于风险状态的价值",可译为受险价值.在险价值.风险价值等. 通常解释为:VaR是在一定置信水平和一定持有 ...
- JavaScript中var关键字的使用详解
作用 声明作用:如声明个变量. 语法 ? 1 var c = 1; 省略var 在javascript中,若省略var关键字而直接赋值,那么这个变量为全局变量,哪怕是在function里定义的. ? ...
- [Algorithm & NLP] 文本深度表示模型——word2vec&doc2vec词向量模型
深度学习掀开了机器学习的新篇章,目前深度学习应用于图像和语音已经产生了突破性的研究进展.深度学习一直被人们推崇为一种类似于人脑结构的人工智能算法,那为什么深度学习在语义分析领域仍然没有实质性的进展呢? ...
- var object dynamic的区别
一.var var本身不是一种类型,只是一种语法糖:var声明的变量在赋值的时候即已决定其变量类型,编译时会进行校验. 二.object object是所以类型的基类,故可以赋任何类型的值. 三.dy ...
随机推荐
- iOS----Xcode6或者Xcode7设置LaunchImage图标
最近设置LaunchImage图标时发现怎么都没有效果,后来发现是Xcode6中新建项目的时候会默认添加一个LaunchScreen.xib的文件,我们启动程序的时候也会发现,加载的时LaunchSc ...
- EasyUI分页索引不能输入非数字
//分页索引不能输入非数字 function PagerCheck() { $(".pagination-num").keydown(function (event) { even ...
- KnockoutJS 3.X API 第四章 数据绑定(3) 控制流if绑定和ifnot绑定
if绑定目的 if绑定一般是格式是data-bind=if:attribute,if后所跟属性或表达式的值应为bool值(也可以是非bool值,当非空字符串时则为真),if绑定的作用与visible绑 ...
- 优化与扩展Mybatis的SqlMapper解析
接上一篇博文,这一篇来讲述怎么实现SchemaSqlMapperParserDelegate——解析SqlMapper配置文件. 要想实现SqlMapper文件的解析,还需要仔细分析一下mybatis ...
- 快速入门系列--GIT版本控制工具
由于GIT刚刚开始使用不久,经常会在Merge时出现没有change-id的情况,在结合gerrit使用时,经常出现不能提交的情形,使得自己很困扰.最近有次熬夜加班,在代码完成后,由于多人在很短时间内 ...
- 线程池ThreadPoolExecutor、Executors参数详解与源代码分析
欢迎探讨,如有错误敬请指正 如需转载,请注明出处 http://www.cnblogs.com/nullzx/ 1. ThreadPoolExecutor数据成员 Private final Atom ...
- 基于Metronic的Bootstrap开发框架经验总结(7)--数据的导入、导出及附件的查看处理
在很多系统模块里面,我们可能都需要进行一定的数据交换处理,也就是数据的导入或者导出操作,这样的批量处理能给系统用户更好的操作体验,也提高了用户录入数据的效率.我在较早时期的EasyUI的Web框架上, ...
- C++和java多态的区别
C++和java多态的区别 分类: Java2015-06-04 21:38 2人阅读 评论(0) 收藏 举报 转载自:http://www.cnblogs.com/plmnko/archive ...
- TortoiseSVN安装以及淘宝 TAE SDK 开发环境的搭建
一.TortoiseSVN 的下载和安装 1.进入TortoiseSVN 官网下载地址http://tortoisesvn.net/downloads.html,根据自己的操作系统位数下载相应最新版本 ...
- webpack打包压缩工具的使用方法
具体使用方法参考来源http://www.cnblogs.com/Leo_wl/p/4793722.html 必须注意的地方: 一.webpack在nodejs环境下运行 二,每个目录下都必须有一个w ...
