PCA(基础知识)

参考：http://blog.csdn.net/wangjian1204/article/details/50642732

参考：https://www.zhihu.com/question/38319536

对角化的概念：

已知n x n的矩阵M，如果对于i≠j,M_ij=0，则该矩阵为对角矩阵，如果存在一个矩阵A，使得A^-1MA的结果为对角矩阵，则称矩阵A将矩阵M对角化。对一个矩阵来说，不一定存在将其对角化的矩阵，但是对于任意一个n x n的矩阵如果存在n个线性不相关的特征向量，则该矩阵可以被对角化。

定理：

令M为n x n矩阵，其特征值为λ₁，λ₂，...，λ_n，特征向量为V₁，V₂，...，V_n，形成线性无关组合，以每个特征向量为列构成矩阵A=[V₁，V₂,...，Vn]，矩阵A可以将矩阵M对角化，乘积矩阵 A^-1MA的主对角元素是矩阵M的特征值：

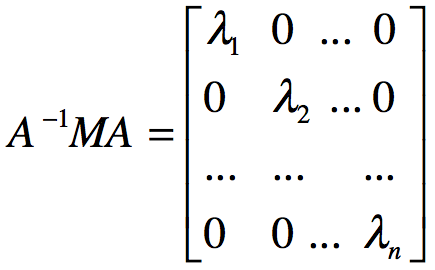
反之，如果存在可逆矩阵A，使得A^-1MA为对角矩阵，则矩阵A的列等于矩阵M的特征向量，A^-1MA的主对角元素为矩阵M的特征值，即M=AΛA^-1。

若M为实对称矩阵，那么M也可以表示为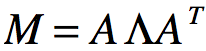：,其中Λ为特征值组成的特征矩阵。因为A为正交矩阵，所以A^T=A^-1

PCA

也称为主成分分析，用于降维和去噪，PCA选取包含信息量最多的方向对数据进行投影，其投影方向可以从最大化方差和最小化投影误差来理解。

假设有n x d矩阵X，每一行是一个d维矩阵x_i，寻找投影方向v_j以最大化投影误差:

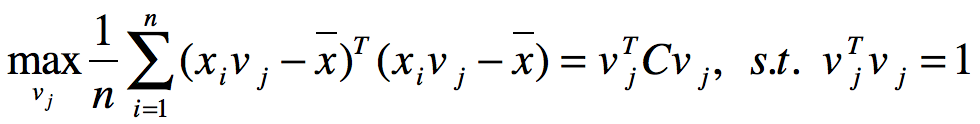该式子同样可以表示成：

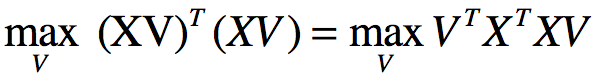，左式的X为样本矩阵

上面第一个式子的右边的推导是基于X已经经过0均值化处理，即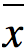为0，v_j是数据的投影方向

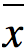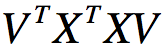从式子可以发现，x_iv_j为样本点x_i在映射维度的坐标，目的就是为了使得投影方差最大化，也即当为0时，求最大化。

那么d x d协方差矩阵C满足

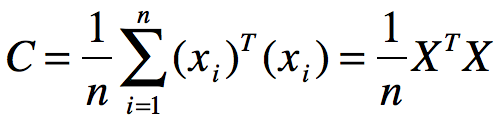,由于C是实对称矩阵，可以进行对角化处理：

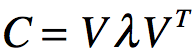
d x d正交矩阵V的每一列是特征向量，d x d矩阵L对角线上的每一个元素是特征值，且特征值按递减顺序排列，将C代回最上式子: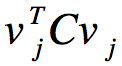

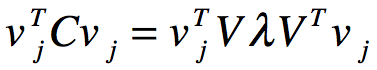
其中λ_j是特征向量v_j对应的特征值，可以发现当投影方向是C的最大特征值对应的特征向量时，投影方向上数据的方差最大，所以用PCA进行降维时选取最大的n个特征值对应的特征向量作为投影方向：XV_k，V_k是最大的k个特征值对应的特征向量矩阵，也就是我们所需要的投影矩阵。

PCA过程与SVD分解的联系在于：

若对X作奇异值分解(SVD)：

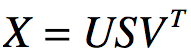
对角矩阵S对角线上的元素是奇异值，U和V是正交矩阵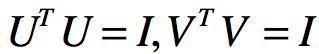：,把X的奇异值分解代入协方差矩阵：

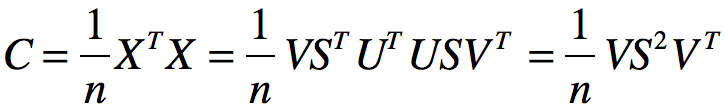
d x d正交矩阵V的每一列是特征向量，特征值和奇异值之间存在对应关系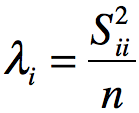：，对X主成份方向进行投影：

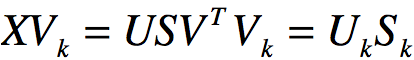
U_k包含U的前k列，S_k包含S左上角的k x k个元素

区别和联系

SVD可以获取另一个方向上的主成分，而PCA只能获取单个方向上的主成分：

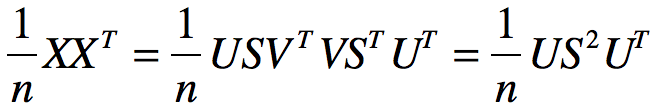
通过SVD可以得到和PCA相同的结果，但是通常SVD比直接使用PCA更加稳定，因为PCA需要计算X^TX的值。