洛谷P1983车站分级

洛谷\(P1983\)车站分级（拓扑排序）

---

目录

• 题目描述

• 题目分析

• 思路分析

• 代码实现

---

题目描述

题目在洛谷\(P1983\)上

​ 题目：

一条单向的铁路线上，依次有编号为 \(1, 2, …, n1,2,…,n\)的 \(n\)个火车站。每个火车站都有一个级别，最低为 11 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 \(x\)，则始发站、终点站之间所有级别大于等于火车站\(x\) 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

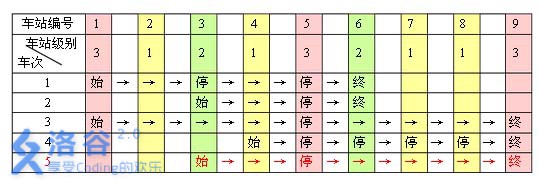
例如，下表是\(5\)趟车次的运行情况。其中，前\(4\)趟车次均满足要求，而第\(5\)趟车次由于停靠了\(3\)号火车站（\(2\)级）却未停靠途经的\(6\)号火车站（亦为\(2\)级）而不满足要求。

现有\(m\) 趟车次的运行情况（全部满足要求），试推算这\(n\)个火车站至少分为几个不同的级别。

​ 输入输出格式：

输入：第一行包含\(2\)个正整数\(n, m\)，用一个空格隔开。

第 \(i + 1\) 行\((1 ≤ i ≤ m)\)中，首先是一个正整数\(s_i(2 ≤ s_i ≤ n)\)，表示第\(i\) 趟车次有\(s_i\) 个停靠站；接下来有\(s_i\)个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出：一个正整数，即\(n\)个火车站最少划分的级别数。

---

题目分析

​ 刚刚看到这道题时，我并没有读懂题，觉得是要用一个\(dp\)或者搜索什么的（也有可能是我搜索题做多了

看到题目，我们知道，假设一个车次从\(x\)车站驶向\(y\)车站，\(c_i\)表示第\(i\)个车站的车站等级。那么中间的\(c_i(x \leq i \leq y)\)一定满足\(c_i\leq c_x\)和\(c_i \leq c_y\)。这样的话，我们就可以构造出一个有向图，级别低的车站指向级别高的车站。这样一来，题目就转化成了拓扑排序的简单题了

---

思路分析

​ 根据上面的题目分析，我们可以得出以下解题方法：

首先将有向图建好，建图的方法是：对于每一个车次，其中停靠的车站我们不能确定与始发站和终点站的关系，那么我们就假设这些车站的等级是相同的，而中间没有停靠的车站则向停靠过的车站（包括始发站和终点站）连一条边。

进行了这项操作之后，我们发现这\(n\)个车站各自有不同的入度，按照入度进行排序，如果有不同的入度，\(ans++\)最后的\(ans\)就是我们要求的答案。

---

代码实现

#include<bits/stdc++.h>
using namespace std;

const int MAXN=3000010;
const int maxn=1005;

int head[MAXN],to[MAXN],nxt[MAXN];
int in[maxn],cnt,dep[maxn];
int a[maxn],flag[maxn],vis[maxn][maxn],ans;
//flag标记是否停靠，vis去重边 

inline void add(int u,int v)
{
    cnt++;
    to[cnt]=v;
    nxt[cnt]=head[u];
    head[u]=cnt;
}//邻接链表存边 

int n,m;

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        memset(a,0,sizeof(a));
        memset(flag,0,sizeof(flag));
        int k;
        scanf("%d",&k);
        for(int j=1;j<=k;j++)
        {
            scanf("%d",&a[j]);
            flag[a[j]]=1;//标记
        }
        for(int j=a[1]+1;j<=a[k];j++)
        {
            if(!flag[j])
            {
                for(int p=1;p<=k;p++)
                {
                    if(!vis[j][a[p]])
                    {
                        in[a[p]]++;
                        add(j,a[p]);
                        vis[j][a[p]]=1;
                    }
                }
            }
        }

    }

    queue<int> q;
    for(int i=1;i<=n;i++)
    {
        if(!in[i]) q.push(i),dep[i]=1;
        //刚开始入度就为0的点深度为1
    }
    while(!q.empty())
    {
        int top=q.front();
        q.pop();
        for(int e=head[top];e;e=nxt[e])
        {
            int v=to[e];
            dep[v]=max(dep[v],dep[top]+1);
            //这个不加max也可以，因为下面的ans已经取过max了
            //不过加上也没问题
            ans=max(ans,dep[v]);//更新答案
            in[to[e]]--;//入度--
            if(!in[to[e]]) q.push(to[e]);
        }
    }
    cout<<ans;

}

这是\(ych\)大神的代码（本蒟蒻表示还不会写）