参考：http://spaces.ac.cn/archives/4062/

参考：https://en.wikipedia.org/wiki/Exterior_derivative

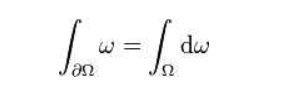
比如Ω是一个曲面（可定向的流行），∂Ω是其边界。w是一个微分形式，dw是一个外微分。

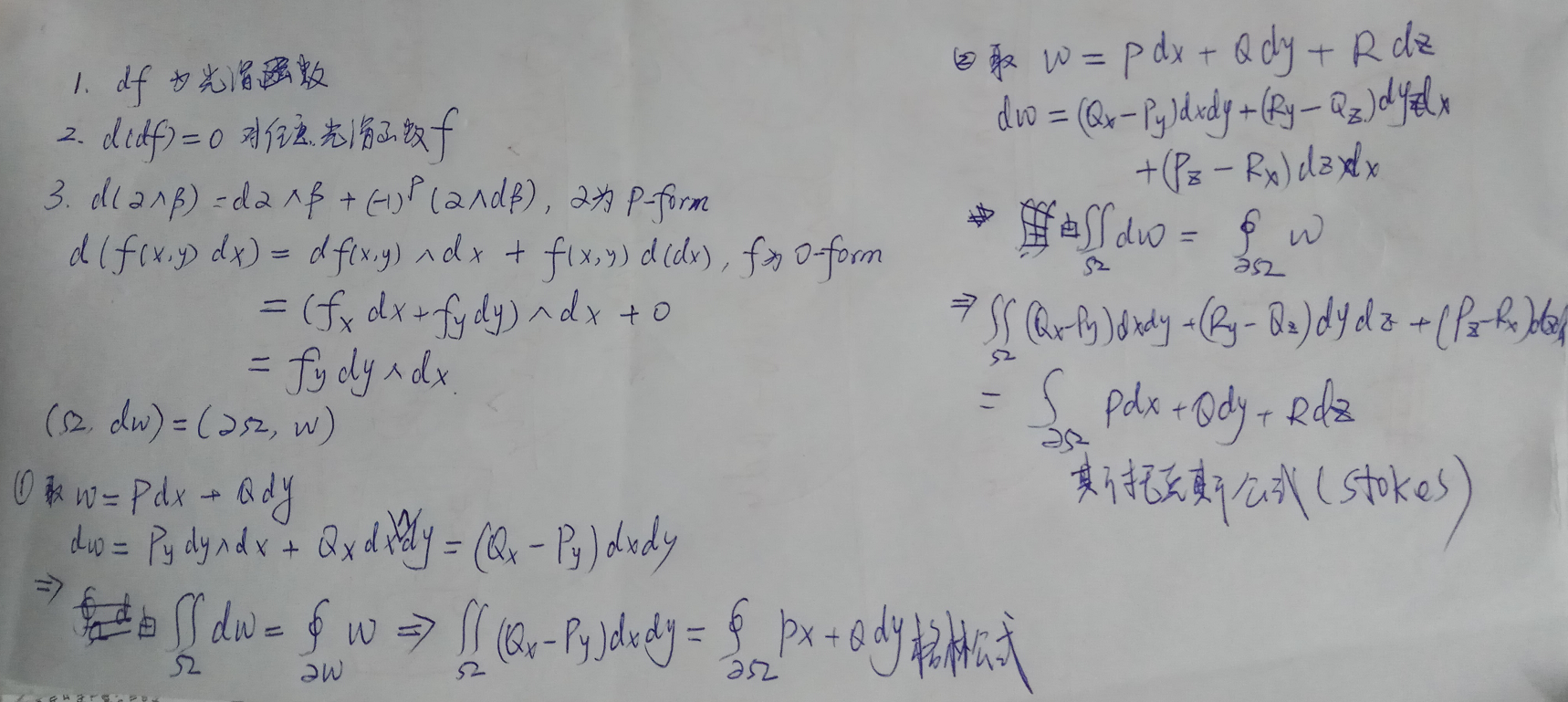
斯托克斯公式（Stokes' theorem）的更多相关文章

  1. 斯托克斯定理（Stokes' theorem）

    1. 几种形式 ∮∂SPdx+Qdy+Rdz=∬S∣∣∣∣∣∣cosα∂∂xPcosβ∂∂yQcosγ∂∂zR∣∣∣∣∣∣dS ∮∂Ωw=∬Ωdw 左边是内积: 右边是外积: 物理上的应用: ∮∂SE ...

  2. 旋度定理(Curl Theorem)和散度定理(Divergence theorem)

    原文链接 首先说说格林公式(Green's theorem).对于一段封闭曲线,若其围城的区域D为单连通区域(内部任意曲线围城的区域都属于院区域),则有如下公式: 其中其中L为D的边界,取正方向.如果 ...

  3. Cauchy-Binet 公式的应用

    Binet-Cauchy 公式 我们知道,方阵的行列式不是方阵的线性函数,即对 \(\forall \lambda\in F,A,B\in F^{n\times n}\),有 \(det(A+B)\n ...

  4. Discrete.Differential.Geometry-An.Applied.Introduction(sig2013) 笔记

    The author has a course on web: http://brickisland.net/DDGSpring2016/ It has more reading assignment ...

  5. How to do Mathematics

    著作权归作者所有.商业转载请联系作者获得授权,非商业转载请注明出处.作者:匿名用户链接:http://www.zhihu.com/question/30087053/answer/47815698来源 ...

  6. WPF实现物理效果 拉一个小球

    一直以来都对物理效果有神秘感,完全不知道怎么实现的.直到看到了周银辉在老早前写的一篇博客:http://www.cnblogs.com/zhouyinhui/archive/2007/06/23/79 ...

  7. 利用Cayley-Hamilton theorem 优化矩阵线性递推

    平时有关线性递推的题,很多都可以利用矩阵乘法来解决. 时间复杂度一般是O(K3logn)因此对矩阵的规模限制比较大. 下面介绍一种利用利用Cayley-Hamilton theorem加速矩阵乘法的方 ...

  8. Matrix_tree Theorem 矩阵树定理学习笔记

    Matrix_tree Theorem: 给定一个无向图, 定义矩阵A A[i][j] = - (<i, j>之间的边数) A[i][i] = 点i的度数 其生成树的个数等于 A的任意n ...

  9. （main）贝叶斯统计 | 贝叶斯定理 | 贝叶斯推断 | 贝叶斯线性回归 | Bayes' Theorem

    2019年08月31日更新 看了一篇发在NM上的文章才又明白了贝叶斯方法的重要性和普适性,结合目前最火的DL,会有意想不到的结果. 目前一些最直觉性的理解: 概率的核心就是可能性空间一定,三体世界不会 ...

随机推荐

  1. P1309 瑞士轮 （吸氧了）

    P1309 瑞士轮 题解 1.这题可以模拟一下 2.sort吸氧可以过(可能是排序有点慢吧,不开会T) sort排序时注意: return 1 是满足条件,不交换 return 0是不满足,交换 代码 ...

  2. 四十二、python中异常

    1.常用异常: AttributeError 试图访问一个对象没有的树形,比如foo.x,但是foo没有属性xIOError 输入/输出异常:基本上是无法打开文件ImportError 无法引入模块或 ...

  3. 2018-5 - 凉经 - Mozilla Firefox Ltd - 前端工程师

    北京谋智火狐信息技术有限公司(北京市东城区建国门华润大厦 17 层)过去面试的时候感觉电梯好神奇啊!一边的电梯是直达 18 层以上的,我按了 18 层准备到了再往下走一层,一个老司机和我说要做另一边的 ...

  4. 阶段3 1.Mybatis_06.使用Mybatis完成DAO层的开发_1 Mybatis中编写dao实现类的使用方式-查询列表

    就是自己写实现类的方式来开发 直接finish 把之前写的CRUD的代码复制到过来. 在把之前pom.xml里面的包的依赖也复制过来 复制到当前的pom.xml内 允许自动导入 以上步骤就是复制了一个 ...

  5. 性能测试工具之WebBench

    一.简介 WebBench是一款在Linux下使用非常简单的压力测试工具.它的原理是:WebBench首先fork出多个子进程,每个子进程都循环做web访问测试.子进程把访问的结果通过pipe告诉父进 ...

  6. sql type subtype 统计

    select * from testtable; type subtype value a sa 1b sb 1a sb errorb sa errora sb 1b sb 1c sa errorc ...

  7. 【MM系列】SAP 物料凭证增强

    公众号:SAP Technical 本文作者:matinal 原文出处:http://www.cnblogs.com/SAPmatinal/ 原文链接:[MM系列]在SAP里查看数据的方法   前言部 ...

  8. 【Qt开发】【VS开发】【Linux开发】OpenCV、Qt-MinGw、Qt-msvc、VS2010、VS2015、Ubuntu Linux、ARM Linux中几个特别容易混淆的内容

    [Qt开发][VS开发][Linux开发]OpenCV.Qt-MinGw.Qt-msvc.VS2010.VS2015.Ubuntu Linux.ARM Linux中几个特别容易混淆的内容 标签:[Qt ...

  9. redis配置主从出现DENIED Redis is running in protected mode

    修改redis配置文件,将绑定的ip给注释掉 #127.0.0.1 在配置文件中将protected-mode 改为no protected-mode no 另一种方式是在配置文件中设置密码 requ ...

  10. C语言第十周作业

        这个作业属于哪个课程 C语言程序设计 这个作业的要求在哪里 https://edu.cnblogs.com/campus/zswxy/computer-scienceclass3-2018/h ...