Softmax函数与交叉熵
在Logistic regression二分类问题中,我们可以使用sigmoid函数将输入Wx+b映射到(0,1)区间中,从而得到属于某个类别的概率。将这个问题进行泛化,推广到多分类问题中,我们可以使用softmax函数,对输出的值归一化为概率值
这里假设在进入softmax函数之前,已经有模型输出C值,其中C是要预测的类别数,模型可以是全连接网络的输出aa,其输出个数为C,即输出为:
所以对每个样本,它属于类别i的概率为:
通过上式可以保证 ,即属于各个类别的概率和为1
对softmax函数进行求导,即求: ,第i项的输出对第j项输入的偏导。代入
softmax函数表达式,可以得到:
求导规则:对于 ,导数为:
所以在我们这个例子中,
上面两个式子只是代表直接进行替换,而非真的等式。 ,(即g(x)=
对
进行求导),要分情况讨论:
- 如果i=j,则求导结果为
- 如果i≠j,则求导结果为0
再来看 对
求导,结果为
所以,当i=j时:(其中,为了方便,令 )
当i≠j时:
标红下,这俩公式很重要:
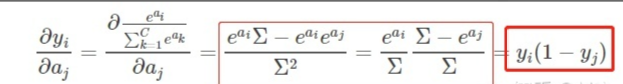
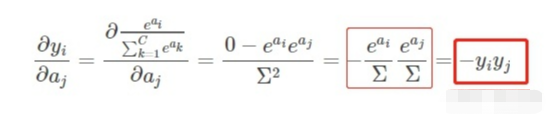
Softmax函数与交叉熵的更多相关文章
- [深度学习] pytorch学习笔记(2)(梯度、梯度下降、凸函数、鞍点、激活函数、Loss函数、交叉熵、Mnist分类实现、GPU)
一.梯度 导数是对某个自变量求导,得到一个标量. 偏微分是在多元函数中对某一个自变量求偏导(将其他自变量看成常数). 梯度指对所有自变量分别求偏导,然后组合成一个向量,所以梯度是向量,有方向和大小. ...
- DL基础补全计划(二)---Softmax回归及示例(Pytorch,交叉熵损失)
PS:要转载请注明出处,本人版权所有. PS: 这个只是基于<我自己>的理解, 如果和你的原则及想法相冲突,请谅解,勿喷. 前置说明 本文作为本人csdn blog的主站的备份.(Bl ...
- 交叉熵和softmax
深度学习分类问题结尾就是softmax,损失函数是交叉熵,本质就是极大似然...
- 关于交叉熵(cross entropy),你了解哪些
二分~多分~Softmax~理预 一.简介 在二分类问题中,你可以根据神经网络节点的输出,通过一个激活函数如Sigmoid,将其转换为属于某一类的概率,为了给出具体的分类结果,你可以取0.5作为阈值, ...
- TF Boys (TensorFlow Boys ) 养成记(五): CIFAR10 Model 和 TensorFlow 的四种交叉熵介绍
有了数据,有了网络结构,下面我们就来写 cifar10 的代码. 首先处理输入,在 /home/your_name/TensorFlow/cifar10/ 下建立 cifar10_input.py,输 ...
- Sigmoid函数与Softmax函数的理解
1. Sigmod 函数 1.1 函数性质以及优点 其实logistic函数也就是经常说的sigmoid函数,它的几何形状也就是一条sigmoid曲线(S型曲线). 其中z ...
- 深度学习原理与框架-神经网络结构与原理 1.得分函数 2.SVM损失函数 3.正则化惩罚项 4.softmax交叉熵损失函数 5. 最优化问题(前向传播) 6.batch_size(批量更新权重参数) 7.反向传播
神经网络由各个部分组成 1.得分函数:在进行输出时,对于每一个类别都会输入一个得分值,使用这些得分值可以用来构造出每一个类别的概率值,也可以使用softmax构造类别的概率值,从而构造出loss值, ...
- 交叉熵的数学原理及应用——pytorch中的CrossEntropyLoss()函数
分类问题中,交叉熵函数是比较常用也是比较基础的损失函数,原来就是了解,但一直搞不懂他是怎么来的?为什么交叉熵能够表征真实样本标签和预测概率之间的差值?趁着这次学习把这些概念系统学习了一下. 首先说起交 ...
- 交叉熵代价函数——当我们用sigmoid函数作为神经元的激活函数时,最好使用交叉熵代价函数来替代方差代价函数,以避免训练过程太慢
交叉熵代价函数 machine learning算法中用得很多的交叉熵代价函数. 1.从方差代价函数说起 代价函数经常用方差代价函数(即采用均方误差MSE),比如对于一个神经元(单输入单输出,sigm ...
随机推荐
- 点云ICP注册
原文链接 背景 两个点云要注册在一块,一般分两个步骤:先做一个大致的对齐,也就是所谓的初始注册,一般可以通过一些可靠的点对来计算得到(如图3所示):然后在初始注册的基础上进行精细注册,提升注册的精度( ...
- USACO4.1 Beef McNuggets【数学/结论】
吐槽/心路历程 打开这道题的时候:*&@#%*#?!这不是小凯的疑惑吗?好像还是个加强版的?我疑惑了.原来$USACO$才是真的强,不知道什么时候随随便便就押中了题目. 对于我这种蒟蒻来说,这 ...
- java中抽象类、接口及区别
转自:http://www.cnblogs.com/dolphin0520/p/3811437.html 一.抽象类 在了解抽象类之前,先来了解一下抽象方法.抽象方法是一种特殊的方法:它只有声明,而没 ...
- [转帖]教你如何修改运行中的docker容器的端口映射
教你如何修改运行中的docker容器的端口映射 在docker run创建并运行容器的时候,可以通过-p指定端口映射规则.但是,我们经常会遇到刚开始忘记设置端口映射或者设置错了需要修改.当dock ...
- numpy-添加操作大全
合并 hstack(tup):按行合并 [前面有个 h,可以理解为 行,这样方便记忆] vstack(tup):按列合并 参数虽然是 tuple,但是 list 也行,可以合并2个或者多个数组. a= ...
- 2017年0406------如何使用sessionStroage来储存参数是对象的,以及localStorage和sessionStorage的不同地方
由于项目需要,需要向另外个页面传参数,,由于参数比较特殊,是对象,所以需要用到sessionStorage方法,下面简单的总结一下方法: (1)这个是要将对象转换成字符串,再存储到storage中, ...
- centos 7下nginx搭建流媒体服务器【动态添加模块】
1.安装nginx依赖包 yum install gcc gcc-c++ openssl-devel zlib-devel pcre pcre-devel yamdi 2.下载解压nginx_mod_ ...
- 085、如何快速部署 Prometheus (2019-05-07 周二)
参考https://www.cnblogs.com/CloudMan6/p/7724576.html 部署环境: 两台 Docker Host 10.12.31.211 10.12.3 ...
- 如何导入GitHub下的vue项目 并启动
如何运行 下载的GitHub项目 一 准备工作: Node.js环境(npm包管理器) vue-cli 脚手架构建工具 cnpm npm的淘宝镜像 二 安装node.js 略 cmd 输入node ...
- PHP实现无限极分类的两种方式
无限极分类说简单点就是一个类可以分成一个分子类,然后一个子类又可以分另一个子类这样无限分下去,就是好象windows可以新建一个文件夹,然后在这个文件夹里又可以建一个文件夹,PHP要实现无限极分类有两 ...
