scipy.sparse 稀疏矩阵

from 博客园（华夏35度）http://www.cnblogs.com/zhangchaoyang 作者:Orisun

本文主要围绕scipy中的稀疏矩阵展开，也会介绍几种scipy之外的稀疏矩阵的存储方式。

dok_matrix

继承自dict，key是(row,col)构成的二元组，value是非0元素。

优点：

非常高效地添加、删除、查找元素
转换成coo_matrix很快

缺点：

继承了dict的缺点，即内存开销大
不能有重复的(row,col)

适用场景：

加载数据文件时使用dok_matrix快速构建稀疏矩阵，然后转换成其他形式的稀疏矩阵

coo_matrix

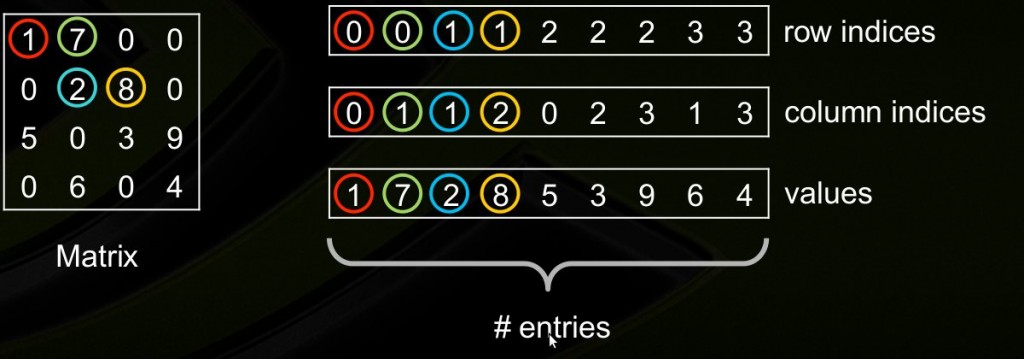
如上图，构造coo_matrix需要3个等长的数组，values数组存放矩阵中的非0元素，row indices存放非0元素的行坐标，column indices存放非0元素的列坐标。

优点：

容易构造
可以快速地转换成其他形式的稀疏矩阵
支持相同的(row,col)坐标上存放多个值

缺点：

构建完成后不允许再插入或删除元素
不能直接进行科学计算和切片操作

适用场景：

加载数据文件时使用coo_matrix快速构建稀疏矩阵，然后调用to_csr()、to_csc()、to_dense()把它转换成CSR或稠密矩阵

csr_matrix

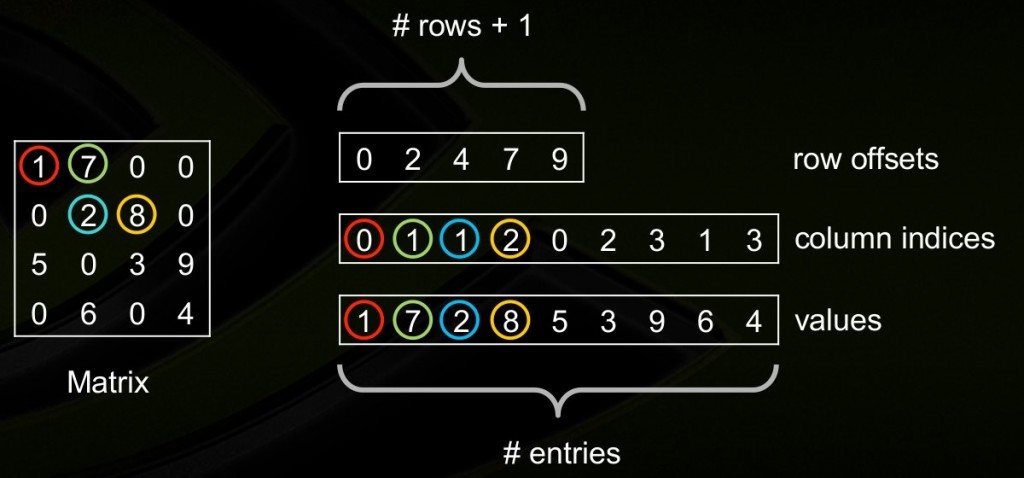
csr_matrix同样由3个数组组成，values存储非0元素，column indices存储非0元素的列坐标，row offsets依次存储每行的首元素在values中的坐标，如果某行全是0则对应的row offsets值为-1（我猜的）。

优点：

高效地按行切片
快速地计算矩阵与向量的内积
高效地进行矩阵的算术运行，CSR + CSR、CSR * CSR等

缺点：

按列切片很慢（考虑CSC）
一旦构建完成后，再往里面添加或删除元素成本很高

csc_matrix

跟csr_matrix刚好反过来。

bsr_matrix

跟CSR/CSC很相近，尤其适用于稀疏矩阵中包含稠密子矩阵的情况。在解决矢量值有限元离散（vector-valued finite element discretizations）这类问题中BSR比CSR/CSC更高效。

dia_matrix

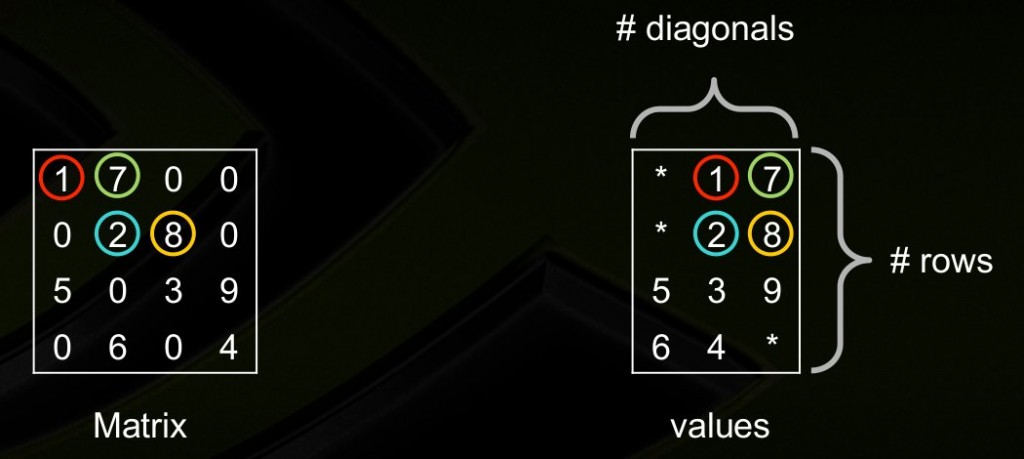
对角线存储法，按对角线方式存，列代表对角线，行代表行。省略全零的对角线。(从左下往右上开始：第一个对角线是零忽略，第二个对角线是5，6，第三个对角线是零忽略，第四个对角线是1，2，3，4，第五个对角线是7，8，9，第六第七个对角线忽略)。[3]

这里行对应行，所以5和6是分别在第三行第四行的，前面补上无效元素*。如果对角线中间有0，存的时候也需要补0。

适用场景：

如果原始矩阵就是一个对角性很好的矩阵那压缩率会非常高，比如下图，但是如果是随机的那效率会非常糟糕。

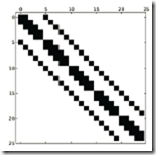
lil_matrix

内部结构是个二维数组:[[(col,value)]]，第一行对应原矩阵的一行（可以快速地定位到行），行内按列编号排序好（通过折半查找可以快速地定位到列），同样只存储非0元素。

优点：

快速按行切片
高效地添加、删除、查找元素

缺点：

按列切片很慢（考虑CSC）
算术运算LIL+LIL很慢（考虑CSR或CSC）
矩阵和向量内和解很慢（考虑CSR或CSC）

适用场景：

加载数据文件时使用lil_matrix快速构建稀疏矩阵，然后调用to_csr()、to_csc()把它转换成CSR/CSC进行后续的矩阵运算
非0元素非常多时，考虑使用coo_matrix（我个人是这样理解的，lil_matrix用一个二维数组搞定，二维数组占用的是连续的内存空间，如果非0元素非常多就要申请一块非常大的连续的内存空间，这样性能很差。而coo_matrix毕竟是使用的3个一维数组，对连续内存空间的要求没那么高）

ELLPACK (ELL)

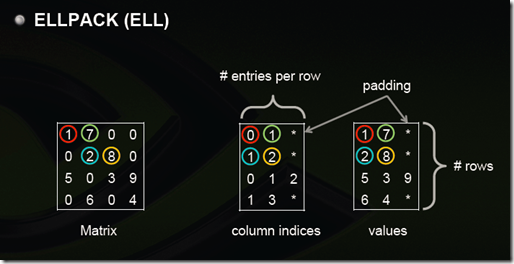
用两个和原始矩阵相同行数的矩阵来存：第一个矩阵存的是列号，第二个矩阵存的是数值，行号就不存了，用自身所在的行来表示；这两个矩阵每一行都是从头开始放，如果没有元素了就用个标志比如*结束。上图中间矩阵有误，第三行应该是 0 2 3。

注：这样如果某一行很多元素，那么后面两个矩阵就会很胖，其他行结尾*很多，浪费。可以存成数组，比如上面两个矩阵就是：

0 1 * 1 2 * 0 2 3 * 1 3 *

1 7 * 2 8 * 5 3 9 * 6 4 *

但是这样要取一行就比较不方便了。

Hybrid (HYB) ELL + COO

为了解决ELL中提到的，如果某一行特别多，造成其他行的浪费，那么把这些多出来的元素（比如第三行的9，其他每一行最大都是2个元素）用COO单独存储。

skyline matrix storage

没看明白，自行wiki。

适用场景：

非常适合于稀疏矩阵的Cholesky分解或LU分解，这两种分解都是用来解线性方程组的。

行列双索引

这是自己实现的一种存储方式，分别按行和按列建立dict（dict中的key是行号或列号），这样按下标查找元素很快，但牺牲了空间。为了挽回空间上的牺牲，我们采用二进制来存储dict中的value。按下标查找元素时，根据行号定位到相应的value，value反序列化后转成dict，该dict的key是列号。

上面的代码中做二进制序列化时用到了struck.pack，来个小例子看下序列化能省多少内存。

优点：

高效地动态添加元素
高效地按下标查找元素
高效地按行切片和按列切片

缺点：

不支持删除元素
内存占用略大

选择稀疏矩阵存储格式的经验

DIA和ELL格式在进行稀疏矩阵-矢量乘积(sparse matrix-vector products)时效率最高，所以它们是应用迭代法(如共轭梯度法)解稀疏线性系统最快的格式
COO格式常用于从文件中进行稀疏矩阵的读写，如matrix market即采用COO格式，而CSR格式常用于读入数据后进行稀疏矩阵计算