HDU-3944 DP?(组合数求模)

一、题目链接

　　http://acm.hdu.edu.cn/showproblem.php?pid=3944

二、题意

　　给一个巨大的杨辉三角，采用类似DP入门题“数字三角形”的方式求从顶点$(0, 0)$到指定点$(n, k)$的最小累加和，输出最小累加和$%p$的结果。其中，$0 \le k \le n \le 10^9,\ p < 10^4,\ and\ p\ is\ a\ prime$。

三、思路

　　一看到数据范围如此之大，直接DP是不行的了。那么就要考虑转换思维和方法，找找规律。先看一张组合数表。

　　

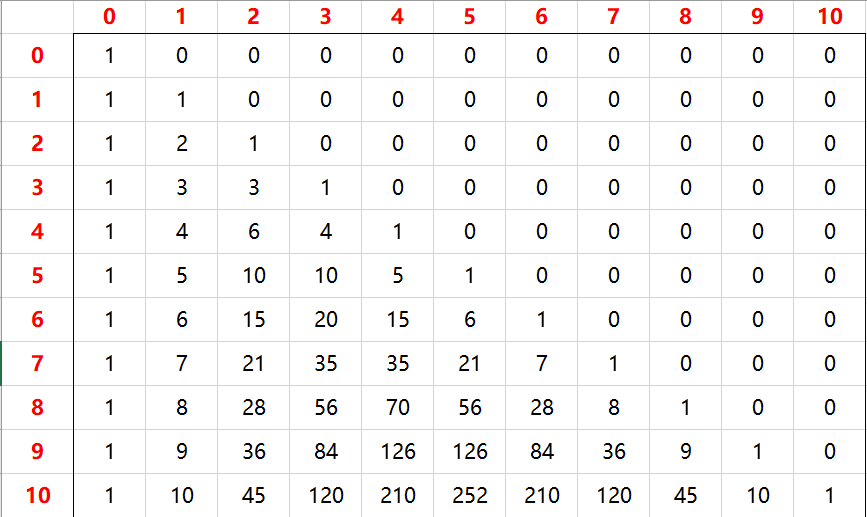
　　从左下部分的杨辉三角中可以看出，从顶点$(0, 0)$到指定点$(n, k)$的最小累加和，一定是走边上。因为边上的数值最小。研究题目给样例可以发现，从顶点$(0, 0)$到$(4, 2)$是由$C_0^0 + C_1^0 + C_2^0 + C_3^1 + C_4^2 = 1+1+1+3+6 = 12$这么来的，由此可以发现一个规律：从顶点$(0, 0)$到指定点$(n, k)$的最小累加和，是先走$n-k$步竖直向下的，每步取最小值$1$，然后再斜向下走一直到$(n, k)$，累加和为$\sum\limits_{i=0}^kC_{n-k+i}^i$。

　　另外，我们可以发现，当$k>\frac{n}{2}$时，先斜向下走到$(k, k)$，再竖直向下走到$(n, k)$，路径上的数值累加和是最小的。由上一篇题解(HDU5226)推导的式子可知，$\sum\limits_{i=k}^{n}C_i^k = C_{n+1}^{k+1} - C_{k}^{k+1} =  C_{n+1}^{k+1}$。

　　找出规律以后，还有一个问题，对于上述一种情况($k \le \frac{n}{2}$)，当$(n, k)$点非常靠右下方的时候，即大约$n \ge 10^8, k \ge 10^8$时，循环累加斜线方向的每一个数值，计算量太大，会超时。所以还需要继续找规律。仔细观察，可以发现，

　　当$j \ge 1$时，$\sum\limits_{i=j}^{k}C_{n-k+i}^i = C_{n+1}^{k} - C_{n-k}^{j-1}$

　　否则，当$j = 0$时，$\sum\limits_{i=j}^{k}C_{n-k+i}^i = C_{n+1}^{k}$

　　由上规律可知：

　　当$k\le \frac{n}{2}$时，先斜向下走到$(n-k, k)$，再竖直向下走到$(n, k)$的最小累加和为\[n-k(从(0, 0)走到(n - k - 1,0))+ \sum\limits_{i=0}^{k}C_{n-k+i}^{i} = (n-k) + C_{n+1}^{k}\]

　　当$k > \frac{n}{2}$时，先斜向下走到$(n-k, k)$，再竖直向下走到$(n, k)$的最小累加和为\[k(从(0, 0)走到(k - 1, k - 1)) + C_{n+1}^{k+1}\]

　　有了上面的式子，求组合数取模就是个很简单的问题了，因为会存在$p < \frac{n}{k}$的情况(这个问题的详细解释在上一篇博客(HDU5226)中已经说了)，所以需要用lucas定理求解。

四、坑点

　　因为这题测试数据量非常大(题目中说了，大约$100000$个测试样例)，我们在用lucas定理的时候，每次都需要预处理阶乘模和阶乘模的逆元，单次测试时间复杂度为$O(p)$，总的时间复杂度为$O(10^5 * p)$，大约$10^9$的运算量，绝对超时。所以，需要再想办法。

　　因为$p$是素数，且$p < 10^4$，我们用筛法统计$10^4$以内的素数个数可以发现，$10^4$以内，只有1231个素数。所以，我们可以预处理出$10^4$内所有数的阶乘模$10^4$内所有素数的数组。但是，素数是离散的，所以，这里需要把所有素数做一下离散化操作。这时，$10^4$内所有数的阶乘模$10^4$内所有素数的数组大小最小是$10^4 * 1231 = 12310000$，如果数据类型为long long，然后再在预处理$10^4$内所有数的阶乘模$10^4$内所有素数的数组的同时预处理出$10^4$内所有数的阶乘模$10^4$内所有素数的逆元数组，大小也是$10^4 * 1231 = 12310000$，加起来就是$2 * 8 * 12310000$个byte，显然会爆内存。解决办法有两个：(1)不要预处理$10^4$内所有数的阶乘模$10^4$内所有素数的逆元数组，需要用逆元时，做一次时间复杂度为$O(log\ p)$的费马小定理或者扩展欧几里得算法；(2)因为$p < 10^4$，所以，可以把数组的数据类型改为int。其实最优的办法是，综合方法(1)和(2)。

五、源代码

　　

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXP 10010
using namespace std;
typedef int LL;
LL n, k, p, facts[MAXP][];
int mp[MAXP], rmp[MAXP], buf[MAXP];
bool is[MAXP];
LL qpow(LL a, LL x, LL mod) {
    LL res = ;
    ) {
        )res = (res * a) % mod;
        a = (a * a) % mod;
        x >>= ;
    }
    return res;
}

void init() {
    fill();
    ] = ] = false;
    ;
    ; i < MAXP; ++i) {
        if(is[i]) {
            for(int j = i + i; j < MAXP; j += i)is[j] = false;
            mp[i] = cnt, rmp[cnt] = i;
            cnt++;
        }
    }

    ; k < cnt; ++k) {
        LL mod = rmp[k];
        facts[][k] = ;
        ; i < MAXP; ++i) {
            facts[i][k] = (facts[i - ][k] * i) % mod;
        }
    }
}

LL C(LL n, LL m) {
    ;
    );
    )return n % p;
    , p) % p * qpow(facts[n - m][mp[p]], p - , p) % p;
}

LL lucas(LL n, LL m) {
    if(n < p && m < p)return C(n, m);
    else return lucas(n / p, m / p) * lucas(n % p, m % p) % p;
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("input.txt", "r", stdin);
#endif // ONLINE_JUDGE
    ;
    init();
    while(~scanf("%I64d %I64d %I64d", &n, &k, &p)) {
        LL ans = ;
        )ans = (n + ) % p;
        )ans = ((n - k) % p + lucas(n + , k) % p) % p;
        , k + ) % p) % p;
        printf("Case #%d: %I64d\n", T++, ans);
    }
    ;
}